线性回归 scikit-learn LinearRegression最小二乘法梯度下降SDG多项式回归学习曲线岭回归Lasso回归

Posted 2021-12-10 wanluN1

github:https://github.com/gaowanlu/MachineLearning-DeepLearning

线性回归 scikit-learn

关键词： LinearRegression、最小二乘法、梯度下降、SDG、多项式回归、学习曲线、岭回归、Lasso回归

LinearRegression

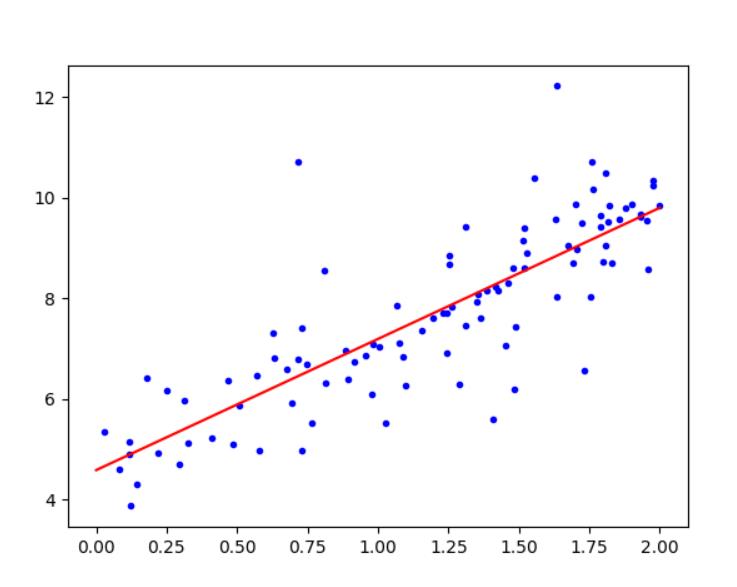
#使用scikit-learn中的线性回归模型
from operator import le
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

#创建数据集
X_train=2*np.random.rand(100,1)
#1000行 每行1列 随机数向量
Y_train=4+3*X_train+np.random.randn(100,1)*np.random.randn(100,1)
print(X_train,Y_train)
#创建模型实例
linearModel=LinearRegression()
linearModel.fit(X_train,Y_train)
#画散点图
plt.plot(X_train,Y_train,"b.")
#使用模型
X_test=[[0],[2]]
Y_pred=linearModel.predict(X_test)
print("斜率= ",linearModel.intercept_,"截距= ", linearModel.coef_)
plt.plot(X_test,Y_pred,"r-")
#限制坐标范围
#plt.axis([0,2,0,15])
plt.show()

最小二乘法

#LinearRegression类基于最小二乘法
import numpy as np
X_train_b = np.c_[np.ones((100, 1)), X_train]
#
theta_best_svd, residuals, rank, s=np.linalg.lstsq(X_train_b,Y_train,rcond=1e-6)
print("最小二乘法 ",theta_best_svd)

伪逆

#numpy计算矩阵伪逆(Moore-Penrose)\\广义逆
X=2*np.random.rand(10,1)
print("计算违逆",np.linalg.pinv(X))

梯度下降

#Numpy进行梯度下降
#data
X=np.random.randn(100,1)
X_b = np.c_[np.ones((100, 1)), X]  # add x0 = 1 to each instance
print(X_b[0])
y=4+3*X+np.random.randn(100,1)
eta=0.1 #learning rate 学习率
n_iterations=10000 #迭代次数
m=100
theta=np.random.randn(2,1) #random initialization
for iteration in range(n_iterations):
    gradients=2/m*X_b.T.dot(X_b.dot(theta)-y)
    theta=theta-eta*gradients
print("梯度下降 theta = ",theta)

随机梯度下降(SDG)

'''
普通的梯度下降，主要问题是用整个训练集来计算每一步的梯度
训练集很大时会很慢。
随机梯度下降，每一步在训练集中随机选择一个实例，并基于该单个实例计算梯度
随机性的好处是可以逃离局部最优，但缺点是永远定位不出最小值。
解决办法：逐步降低学习率，开始步长比较大、越来越小，靠近全局最优、模拟退火。
'''
theta_path_sgd = []#记录中间迭代的过程
#data
X=np.random.randn(100,1)
X_b = np.c_[np.ones((100, 1)), X]
y=4+3*X+np.random.randn(100,1)
n_epochs=50
m=len(X_b)
t0,t1=5,50 # learning schedule hyperparameters(学习进度超参数)
def learning_schedule(t):
    return t0/(t+t1)
theta=np.random.randn(2,1) #定位初始化
#50次迭代
for epoch in range(n_epochs):
    for i in range(m):#每次进行m个回合的迭代，每个回和称为一个轮次
        random_index=np.random.randint(m)#随机选实例
        xi=X_b[random_index:random_index+1]
        yi=y[random_index:random_index+1]
        gradients=2*xi.T.dot(xi.dot(theta)-yi)#用此实例计算梯度
        eta=learning_schedule(epoch*m+i)#计算学习率
        theta=theta-eta*gradients
        theta_path_sgd.append(theta)#记录迭代的中间结果
print(f"theta={theta}")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("y", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
#画出迭代过程
for i in range(len(theta_path_sgd)):
    x_draw=[[0],[2]]
    y_draw=[[theta_path_sgd[i][0][0]],[2*theta_path_sgd[i][1][0]+theta_path_sgd[i][0][0]]]
    plt.plot(x_draw,y_draw,"r-")
    if(i>50):#只画出前50次
        break
plt.plot(X,y,"b.")
plt.show()



#Scikit-Learn中的随机梯度下降
from sklearn.linear_model import SGDRegressor 
X=np.random.randn(100,1) 
y=4+3*X+np.random.randn(100,1)
#SGDRegressor 参数解释
'''
迭代1000轮次
损失下降小于0.001为止
以eta0=0.1学习率开始
不使用正则化 penalty=None
'''
sgd_reg=SGDRegressor(max_iter=1000,tol=1e-3,penalty=None,eta0=0.1)
sgd_reg.fit(X,y.ravel())#.ravel()将多维数组转为一维
print(sgd_reg.intercept_)#intercept（截距）
print(sgd_reg.coef_) #系数（斜率）
plt.plot(X,y,"b.")
x_draw=[[0],[2]]
y_draw=[[sgd_reg.intercept_[0]],[2*sgd_reg.coef_[0]+sgd_reg.intercept_[0]]]
plt.plot(x_draw,y_draw,"r-")
plt.axis([0, 2, 0, 15])#坐标系显示范围
plt.show()

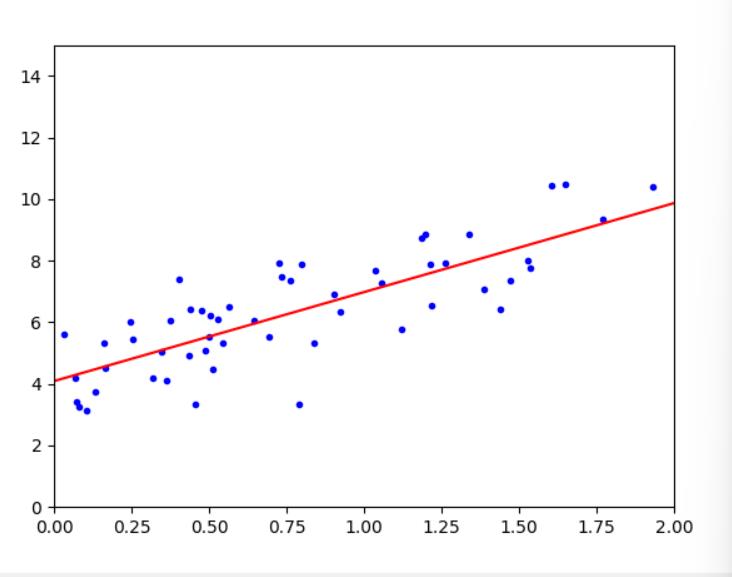
小批量梯度下降

'''
普通的梯度下降是使用全部训练集求梯度，随机梯度下降是随机选一个实例，
小批量梯度下降是在随机梯度下降的基础上每次随机选一小部分实例求梯度
'''

多项式回归

'''
使用线性模型来拟合非线性数据，在非线性方程特征集上训练一个线性模型，这种技术称为多项式回归。
'''
m=100
X=6*np.random.rand(m,1)-3
y=0.7*X**2+X+3.6+np.random.randn(m,1)
plt.plot(X,y,"b.")
'''
当存在多个特征时，多项式回归能够找到特征之间的关系（这是普通线性回归模型无法做到的）。
PolynomialFeatures还可以将特征的所有组合添加到给定的多项式阶数。
例如，如果有两个特征a和b，则degree=3的PolynomialFeatures不仅会添加特征a^2、a^3、b^2和b^3，
还会添加组合ab、a^2b和ab^2  PolynomialFeatures（degree=d）
可以将一个包含n个特征的数组转换为包含 阶乘(n+d)/(阶乘d * 阶乘 n) 个特征的数组
'''
from sklearn.preprocessing import PolynomialFeatures# Polynomial Features（多项式特征）
from sklearn.linear_model import LinearRegression #线性回归
poly_features=PolynomialFeatures(degree=2,include_bias=False)
X_poly=poly_features.fit_transform(X)#多项式特征
#使用线性模型
lin_reg=LinearRegression()
lin_reg.fit(X_poly,y)
print(lin_reg.intercept_,lin_reg.coef_)
#[2.14407795] [[0.8758063  0.48173944]] y=0.48*x**2+0.87*x+2.14
#画出拟合的曲线
x_draw=[]
y_draw=[]
x=-100
while x<=100:
    x_draw.append(x)
    y_=lin_reg.coef_[0][1]*x**2+lin_reg.coef_[0][0]*x+lin_reg.intercept_[0]
    y_draw.append(y_)
    x=x+0.1
plt.plot(x_draw,y_draw)
plt.axis([0, 2, 0, 15])#坐标系显示范围
plt.show()

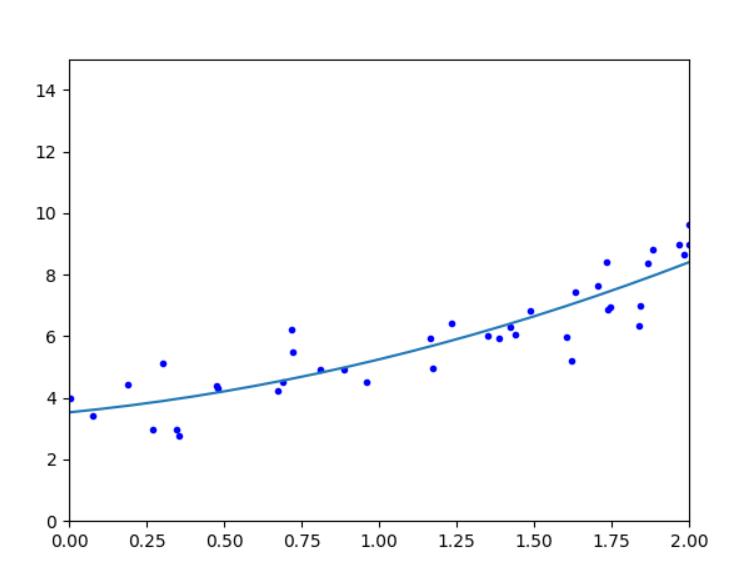
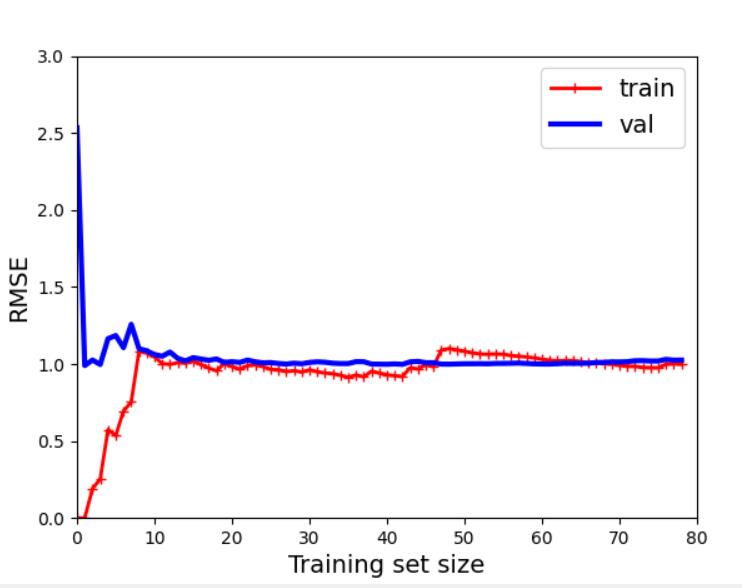
学习曲线

'''
欠拟合与过拟合
如果模型在训练数据上表现良好，但根据交叉验证的指标泛化较差，
则你的模型过拟合。如果两者的表现均不理想，则说明欠拟合。
* 均方误差 mean squared error
* 训练测试分 train_test_split
'''
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

X=np.random.randn(100,1)
y=4+3*X+np.random.randn(100,1)
#learning_curves 学习曲线
def plot_learning_curves(model,X,y):
    X_train,X_val,y_train,y_val=train_test_split(X,y,test_size=0.2)
    train_errors,val_errors=[],[]
    #使用交叉验证
    for m in range(1,len(X_train)):#从使用两个数据开始拟合
        model.fit(X_train[:m],y_train[:m])#使用前m个训练集
        y_train_predict=model.predict(X_train[:m])#得出前m个训练集y的预测值
        y_val_predict=model.predict(X_val)#获得验证集预测值
        #训练集均方误差
        train_errors.append(mean_squared_error(y_train[:m],y_train_predict))
        #使用mean_squared_error获得训练集预测值均方误差
        #测试集均方误差
        val_errors.append(mean_squared_error(y_val,y_val_predict))
        #使用mean_squared_error获得验证集预测值均方误差
    plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
    plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
    plt.legend(loc="upper right", fontsize=14)   # 曲线标注
    plt.xlabel("Training set size", fontsize=14) # x轴标签
    plt.ylabel("RMSE", fontsize=14)              # y轴标签
    plt.axis([0, 80, 0, 3])
    plt.show()
#线性回归模型实例
lin_reg=LinearRegression()
#调用学习曲线函数
plot_learning_curves(lin_reg,X,y)
'''
可见数据欠拟合，训练集的误差小于测试集的误差，且训练集曲线与检验集曲线中间
的距离较近，使用再多的数据集训练也是无济于事
'''
#10阶多项式模型的学习曲线
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures# Polynomial Features（多项式特征）
#定义流水线
polynomial_regression=Pipeline([
    ("poly_features",PolynomialFeatures(degree=10,include_bias=False)),#多项式特征
    ("lin_reg",LinearRegression())#线性模型
])
plot_learning_curves(polynomial_regression,X,y)
#在训练集上面的误差很小，在测试集上面的误差较大，过拟合，使用更大的数据集
# 则两条曲线会继续接近

正则化线性模型

'''岭回归Ridge闭式求解'''
from sklearn.linear_model import Ridge
#创建岭回归实例
ridge_reg=Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X,y)
print(ridge_reg.predict([[1.5]]))


'''岭回归Ridge随机梯度下降'''
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(penalty="l2", max_iter=1000, tol=1e-3, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
'''
超参数penalty设置的是使用正则项的类型。设为"l2"表示希望SGD在成本函数中添加
一个正则项，等于权重向量的 2范数的平方的一半，即岭回归。
'''

'''Lasso回归'''
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])