数据结构堆排序
Posted 凛音Rinne
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构堆排序相关的知识,希望对你有一定的参考价值。
堆排序
-
因为大堆和小堆只能知道最大元素和最小元素
-
而TopK也只能找出前k个大/小的元素
这一篇,同时满足上面两个求
本篇有大量内容在前两篇文章基础上:
以及很多代码的接口/函数之前写过不再重复:
一、思路
1. 建小堆
排序按从小到大排序,我们可能先需要一个小堆
调整堆的顺序有两种操作方式,向上调整和向下调整
向上调整建小堆:
类似于之前在堆后插入一个数,然后进行
向上调整//堆排序 void Heapsort(int* a, int n) { int i = 0; for (i = 1; i < n; i++) { AdjustUp(a, i); } }
向下调整建小堆:
调整每一个非叶子节点,将其变成小堆,多个小堆在一起,也就是小堆了
最后一个叶子节点就是最后一个节点的父节点
//向下调整 int i = 0; for (i = (n - 2) / 2; i >= 0; i--) { AdjustDown(a, n, i); }
然后就发现,建了一个小堆,再往下操作只能是后面n - 1再进行建堆……这也太麻烦了
变换思路,改建大堆
2. 建大堆
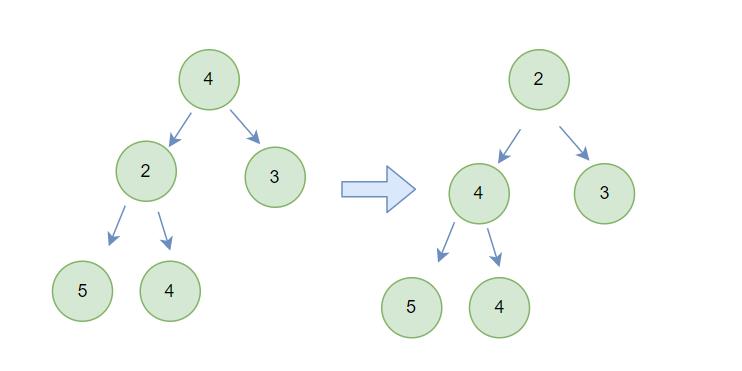
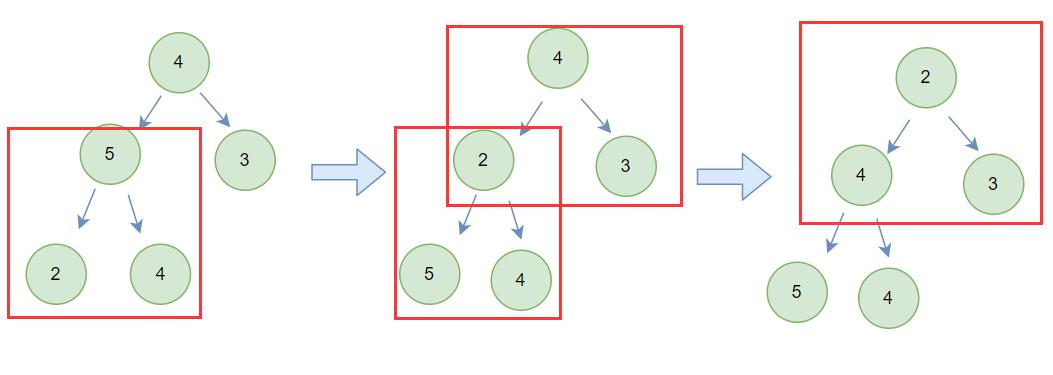
根据之前,pop堆顶元素的原理
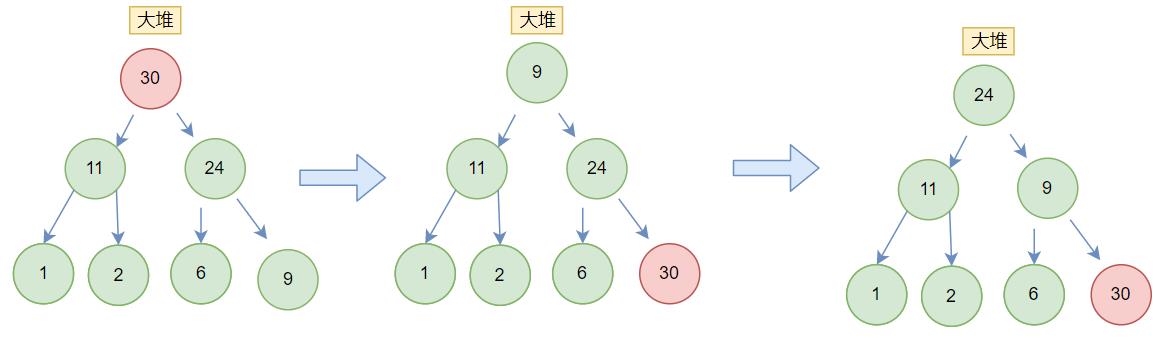
先把最后一个元素和根交换,再pop掉原来的根,新的根进行向下调整
这里我们不pop掉原来的根,进行向下调整的堆变成前n-1个数的堆里向下调整

for (i = 0; i < n; i++)
{
swap(&a[0], &a[n - 1 - i]);
AdjustDown(a, n, i);
}
3. 测试代码
//堆排序
void Heapsort(int* a, int n)
{
向上调整
//int i = 0;
//for (i = 1; i < n; i++)
//{
// AdjustUp(a, i);
//}
//向下调整
int i = 0;
for (i = (n - 2) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
for (i = 0; i < n; i++)
{
swap(&a[0], &a[n - 1 - i]);
AdjustDown(a, n - i - 1, 0);
}
}
//测试堆排序
void testsort()
{
int n = 7;
int a[7] = { 1, 5, 6, 2, 4, 6, 7 };
Heapsort(a, n);
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\\n");
}
int main()
{
testsort();
return 0;
}
测试结果:
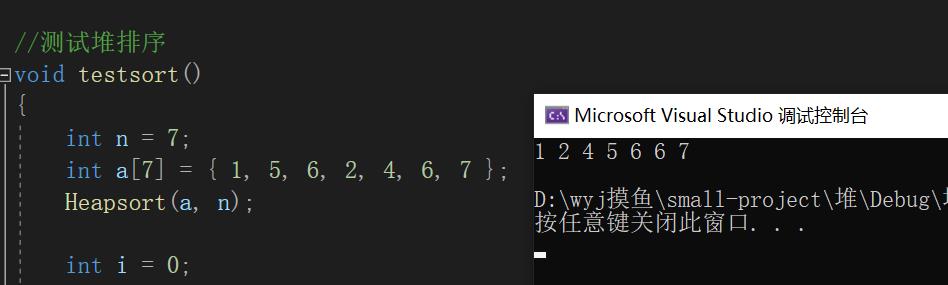
可以看出数组变成升序了
二、证明时间复杂度
1. 建堆过程
以小堆为例,最坏的情况就是下面全是大的
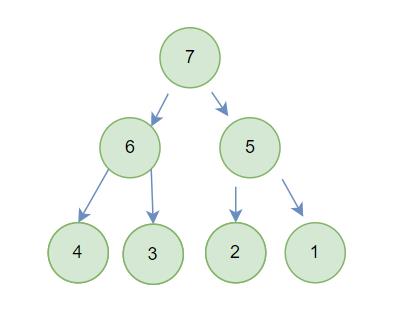
- 第
1层,20 个节点,需要向下移动h-1层 - 第
2层,21 个节点,需要向下移动h-2层
…… - 第
h-1层, 2h-2 个节点,需要向下移动1层 最后一层不用动
T(n) = 20 * (h-1) + 21 * h-2 + …… + 2h-2 * 1
利用高中等差x等比形式的求和,错位相减法

建堆的时间复杂度为O(n)
2. 向下调整过程
向下调整时间复杂度为o(n),一共n个数
所以是nlog2(n)
以上是关于数据结构堆排序的主要内容,如果未能解决你的问题,请参考以下文章
14.VisualVM使用详解15.VisualVM堆查看器使用的内存不足19.class文件--文件结构--魔数20.文件结构--常量池21.文件结构访问标志(2个字节)22.类加载机制概(代码片段