用C程序解决汉诺塔问题与青蛙跳台阶问题（递归）

Posted 2021-12-10 东辰良月2

一.汉诺塔问题

  汉诺塔是一种古印度游戏，该游戏的实质就是在一块木板上有三根固定的柱子

而在左边的柱子上有着n个大小不同的圆盘，我们需要做就是把左边所有的盘子全部移到右边的柱子上。操作规则：1.圆盘在柱子上必须按照从大到小（大圆盘在下）依次排列。2.每次只能移动圆柱最上面的圆盘。

问题分析：先假设三根柱子分别为“A”"B""C",A柱有着所有的初始盘，我们的目的就是把A柱上的所有盘子全部移到C柱上。

n=1时，直接把圆盘从A柱移动到C柱就可。

n=2时，A-->B,A-->C,B-->C。（在这操作中B为中转柱）

n=3时，A-->C,A-->B,C-->B,①A-->C,B-->A,B-->C,A-->C。对n=3这种情况进行分析：在①之前圆盘所在圆柱的情况有两种：

1.是所有圆盘在A,B,C三个圆柱中都有一个圆盘。

2.是A，C上有圆盘而B上没有圆盘。

由此可知在①前B柱是中转柱；在①之后也有两种情况：

1.只有B,C上有圆盘。

2.A,B,C上都有一个圆盘。

并且我们的游戏目标从一开始的把A上所有圆盘移到C柱（A-->C）,变成了把B上所有圆盘移到C柱上（B-->C）,而在这时中转柱是A柱。

......

直到A上有n个圆盘时,现在对n这种情况进行分析：想要把n个圆盘从A柱移到C柱上有三大步骤：

①将A上n-1个圆柱全部移到C柱上（中转柱B柱）。

②将A上的一个圆盘移到C柱上。

③将B上n-1个圆盘全部移到C柱上（中转柱A柱）。

在这要穿插一下递归的主要思想就是大事化小。现在将①步骤分为三个小步骤：

①将A上n-2个圆盘全部移到C柱上（中转柱B柱）。

②将A上第n-1个圆盘移到B柱上。

③将C上n-2个圆盘移到A柱上（中转柱A柱）。

然后将第二个①化为更小的三个步骤......就这样一步步大事化小。

代码实现：

#include<stdio.h>

void hanoi(int n, char post_1, char post_2, char post_3)
{
    if (n == 1)
    {
        printf("%c --> %c\\n", post_1, post_3);
    }
    else
    {
        hanoi(n - 1, post_1, post_3, post_2);
        printf("%c --> %c\\n", post_1, post_3);
        hanoi(n - 1, post_2, post_1, post_3);
    }
}


int main()
{
    int n = 0;
    char a = 'A', b = 'B', c = 'C';
    scanf("%d", &n);
    hanoi(n, a, b, c);
    return 0;
}

 二.青蛙跳台阶问题

  一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级台阶有多少种跳法？（实质就是斐波那契数列的变种）

问题分析：

我们不妨列举一下n比较少的情况时的跳法：

①n=1时，1种跳法。          ②n=2时，有2种跳法。

③n=3时，有3种跳法。      ④n=4时，有5种跳法。

⑤n=5时，有8种跳法。

......

很明显，同过观察上面列举的情况可以发现：

n=3时所有的跳法等于n=1时和n=2时的所有跳法之和；

n=4时的所有跳法等于n=2和n=3时的所有跳法之和；

......

以此类推可以得出f(n)=f(n-1)+f(n-2) (n>2)。（f(n)为跳法数量）

 

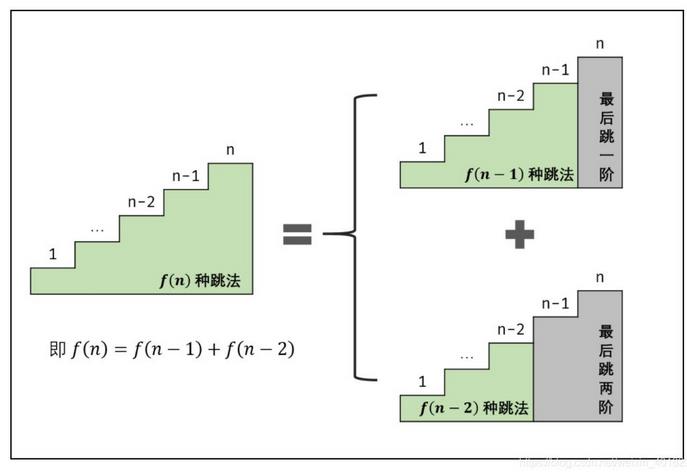
代码实现：

#include<stdio.h>

int frogjump(int n)
{
	if (n == 1)
	{
		return 1;
	}
	else if (n == 2)
	{
		return 2;
	}
	else
	{
		return frogjump(n - 1) + frogjump(n - 2);
	}
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	printf("%d", frogjump(n));
	return 0;
}