递归中两个经典的汉诺塔和青蛙跳台阶问题

Posted 2021-09-10 呆呆兽学编程

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了递归中两个经典的汉诺塔和青蛙跳台阶问题相关的知识，希望对你有一定的参考价值。

汉诺塔

什么是汉诺塔？

相信大家对汉诺塔这个游戏不陌生吧，或多或少都玩过一些。

这是一种益智游戏，游戏规定要把一个柱子上的所有盘子移动到另一个柱子上，每次只能移动一块，且要保证每次移动过程中小盘子在大盘子上面。

递归实现汉诺塔问题

递归的思想就是大事化小。所以问题我们可以这样考虑

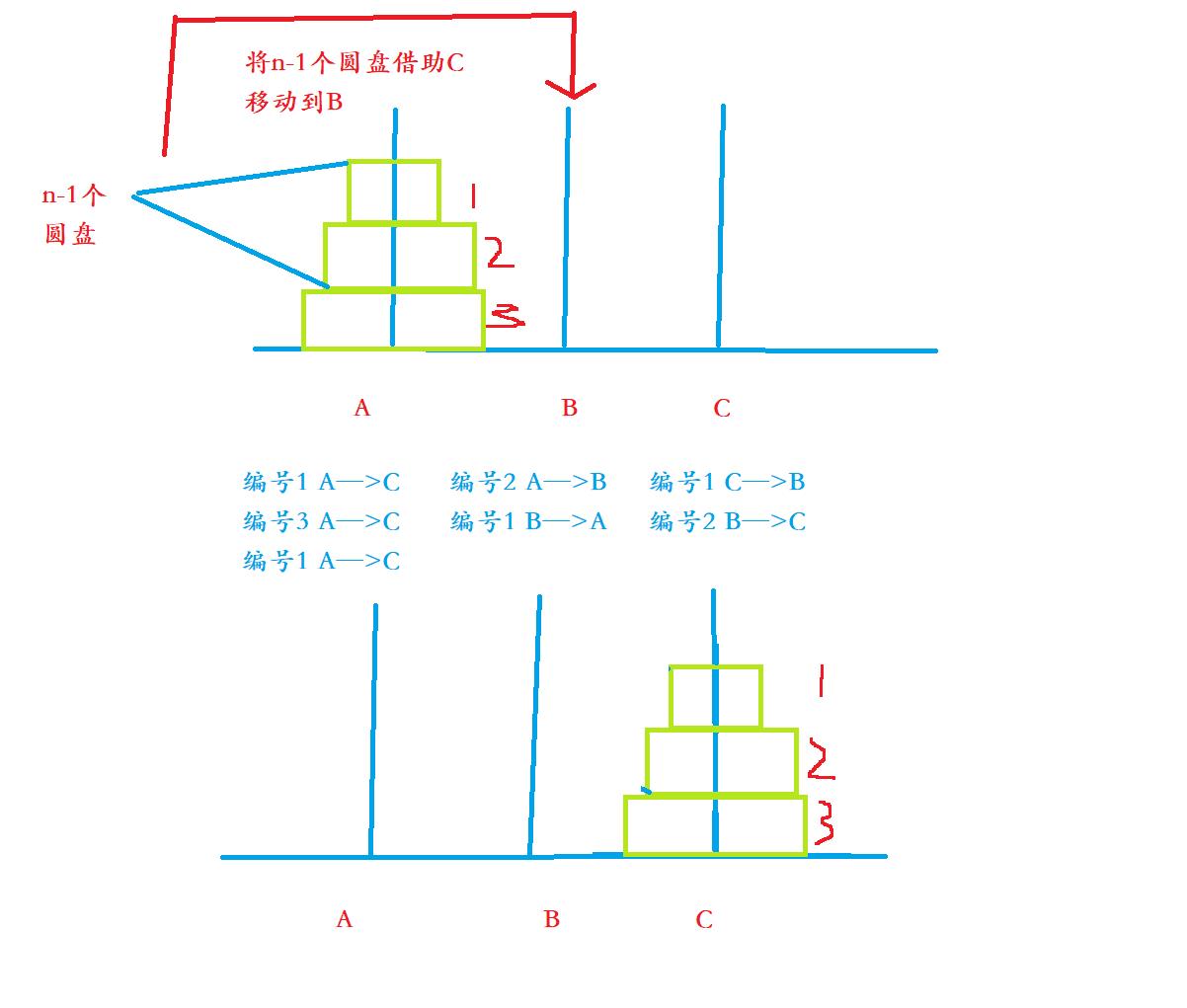
有三个柱子分别是A B C 将A柱子上n个盘子借助B柱子移动到C柱子上
我们可以将这个问题转化为
将A柱子上n-1个盘子借助C柱子移动到B柱子上，然后将最大的那一个盘子直接移动到C盘
n-1个圆盘的汉诺塔问题
进而转化为
将A柱子上n-2个盘子借助A柱子移动到C柱子上的问题 n-2个圆盘的汉诺塔问题
……
最后就是1个圆盘的汉诺塔问题

这就是思想，我们来考虑一个简单的，三个圆盘的

代码实现如下：

void Hanoi(int n, char A, char B, char C,int* count)
{
	if (n == 1)
	{
		printf("将编号为%d的盘子从%c柱子上移动到%c柱子上\\n", n, A, C);
		(*count)++;
	}
	else
	{
		//将A柱子上n-1个盘子借助C柱子移动到B柱子上
		Hanoi(n - 1, A, C, B,count);
		//将A柱子上1个盘子直接移动到C柱子上
		printf("将编号为%d的盘子从%c柱子上移动到%c柱子上\\n", n, A, C);
		(*count)++;
		//将B柱子上n - 1个盘子借助A柱子移动到C柱子上
		Hanoi(n - 1, B, A, C,count);
	}
}
void TestHanoin()
{
	int n = 0;
	int count = 0;//记录移动步数
	char A = 'A';
	char B = 'B';
	char C = 'C';
	printf("请输入汉诺塔上要移动盘子的个数:");
	scanf("%d", &n);
	printf("移动情况如下:\\n");
	Hanoi(n, A, B, C, &count);
	printf("移动步数为:%d\\n", count);
}
int main()
{
	TestHanoin();
	return 0;
}

青蛙跳台阶

青蛙跳台阶问题简述

有n阶台阶，青蛙每次跳一步或者两步，要求我们计算有多少种跳法。

递归实现青蛙跳台阶问题

递归思想如下：

跳到最后一个台阶有两种：
1、从n-1个台阶跳上去
2、从n-2个台阶跳上去
假如把n阶台阶的跳法数叫f(n),那么跳到n-1阶台阶的跳法数有f(n-1)，跳到n-2阶台阶的跳法数有f(n-2)。
所以可以得出: f(n)=f(n-1)+f(n-2)（n>2）
f(1)=1 f(2)=2
这样就可以一直递归求解下去的出答案了

其实递归用到的是一种伪算法，我们先想出了这个函数的功能，然后层层调用的过程中有实现了这个算法，这就是递归的妙处，将大事化小。

代码是先如下：

int FrogJump(int n)
{
	//跳到最后一个台阶有两种：
	//1、从n-1个台阶跳上去
	//2、从n-2个台阶跳上去
	//得出递归函数：f(1)=1  f(2)=2 f(n)=f(n-1)+f(n-2)
	if (n == 0)
	{
		return 0;
	}
	else if (n == 1)
	{
		return 1;
	}
	else if (n == 2)
	{
		return 2;
	}
	else
	{
		return FrogJump(n - 1) + FrogJump(n - 2);
	}
}
void TestFrogJump()
{
	int n = 0;
	int count = 0;//记录跳台阶种数
	printf("请输入台阶数:");
	scanf("%d", &n);
	count = FrogJump(n);
	printf("青蛙跳%d阶台阶跳法种数为：%d\\n", n, count);
}

int main()
{

	TestFrogJump();

	return 0;
}