递归经典例题详解（汉诺塔问题斐波那契数列问题青蛙跳台阶问题）

Posted 2021-09-06 watermelonw

1、汉诺塔问题

问题背景：

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。游戏的目标:把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

（来自360百科）

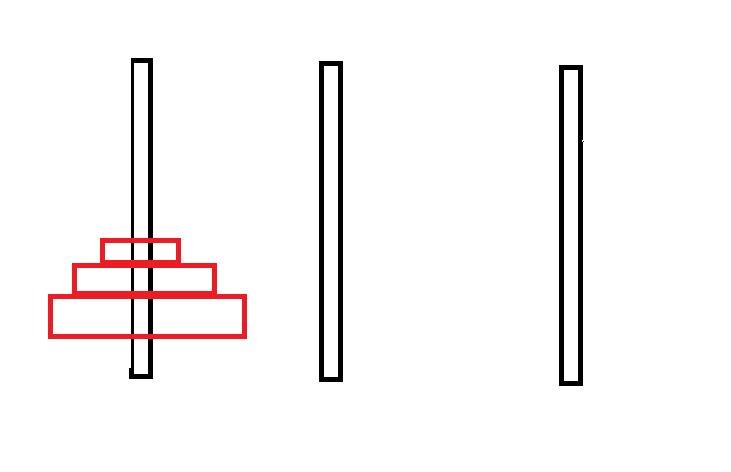
                                                A                    B                       C

首先分析一下问题：

题目中我们有一个十分重要的限制条件，就是在我们移动铜板的时候，一定要小的铜板在大的铜板上面

依据这个，我们可以简单的有图像来展现我们的想法（图有点丑，各位见谅哈）：

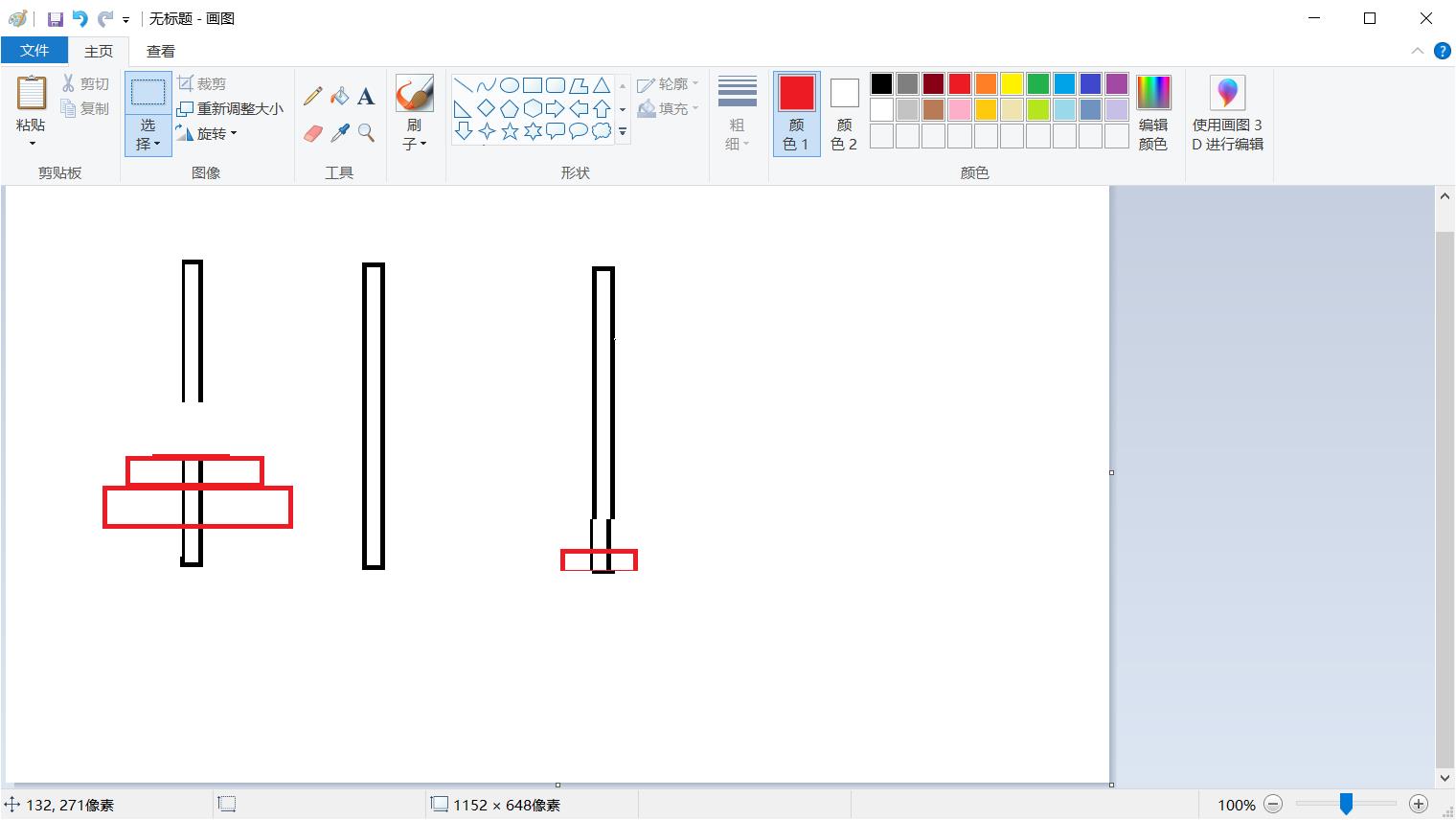
1、从A将最小块移动到C上

  

2、从A将中间块移动到B上

 

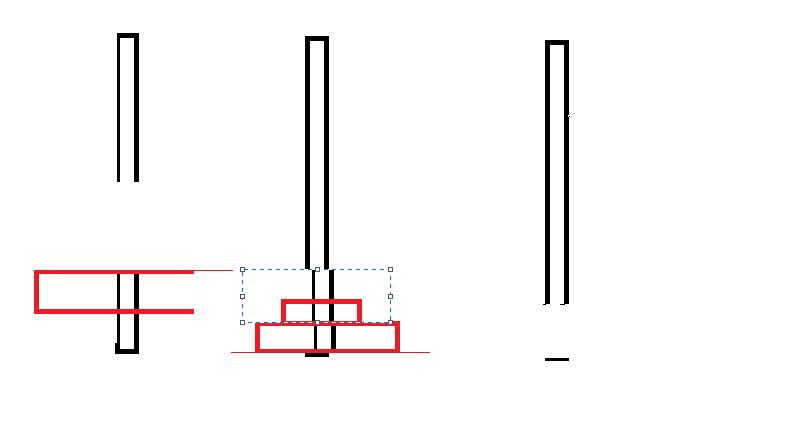
3、从C将最小块移动到B上

 4、从A将最大块移动到C上

 

  

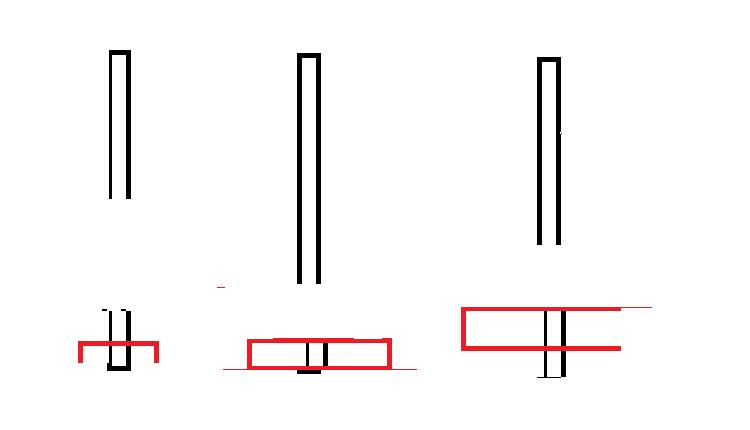
5、从B将最小快移动到A上面

  

6、从B 将中块移动到C上

  

 7、从A将最小快移动到C上

透过方法对其中的算法进行分析 ：

通过图解我们可以知道，在前三步中我们所做就是将最上面的两块移动到另外两个柱子中的一个。在第四步中将最大块移动到另外一个柱子上面。在后三步中将另外上面的两块移动到大块的上面。

通过上面分析，我们可以再进一步抽象成数学模型来更加深入了解一下

前三步我们可以理解为是将上面两块进行一个汉诺塔问题的运作，然后中间一步是将大块移动到另外一块上面，然后最后三步是将另外两块再做一次汉诺塔问题的运作。这样就完成了三块的汉诺塔问题运作。

进而我们可以把三块推广到更为普遍的n块来分析

简单的理解就是先将上面n-1块进行汉诺塔的运作，然后将最下面的第n块放到另外一个柱子上面，最后将上面n-1块再次汉诺塔运作放在最大快的上面。

至此我们对其中的算法已经分析完毕，建立起了数学模型，接下来我们探讨一下，再进行汉诺塔问题是n块的操作步数的计算分析：

我们可以设n块时候的操作步数为f(x);

f(x)=f(x-1)+1+f(x-1)=2f(x-1)+1

当x=0；f(x)=0;

当x=1；f(x)=1;

当x=2；f(x)=3;

当x=3；f(x)=7;

.......................

通过适当分析可知，[f(x)-1]是2的指数式增长，据此我们可以抽象出其中的数学模型为

   x>=1  f(x)=2^x-1

   x=0  f(x)=0

到此我们的分析已经全部结束了，接下来就是我们代码实现的过程了    

void move(char from , char to)
{
    printf("将%c柱子最上面的圆盘->放到%c柱子上面\\n", from, to);
}
void hanoi(char A,char B,char C,int n)           //函数目的将n个圆盘按照汉诺塔规则从A柱子移动到C柱子上面(函数默认最开始都在A上最后移动到B上面)   
{
    if (n == 1)
    {
        move(A, C);
    }
    else
    {
        hanoi(A,C,B,n - 1);
        move(A, C);
        hanoi(B, A, C, n - 1);
    }
}
int main()
{
    char A = 'A';
    char B = 'B';
    char C = 'C';   //ABC分别表示三个柱子
    int n = 0;
    printf("请输入汉诺塔的圆盘个数:\\n");
    scanf("%d", &n);  //n为有几个圆盘
    hanoi(A,B,C,n);     //调用汉诺塔函数函数给出步骤

}

 

---

 2、斐波那契数列

 背景介绍：

 该数列提出者意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci）提出的，该数列又称为黄金分割数列，其基本排列为：

1，1，2，3，5，8，13.......(j简而言之就是从第三个开始该数是前两个数之和)

（来自360百科）

算法分析：

首先我们分析可知第n个数为前两个数之和那么用数学语言表达就是

fib(n)=fib(n-1)+fib(n-2)  [这里的n>2]

 其实这里这里的递归思维就已经产生了，我们可以将求第n个数转化成求n-1和n-2,并无限的这样下分下去直到第一个第二个数，这样我们的数学模型就建立出来了，下面就是代码实现了

1、递归的方法求斐波那契数列
int fib(m)
{
	int a = 1;
	int b = 1;
	if (m > 2)
		return fib(m - 1) + fib(m - 2);
	else 
		return 1;
}
int main()
{
	int m = 0;
	scanf("%d", &m);
	int ret=fib(m);
	printf("%d", ret);
	return 0;
}

 

备注： 在这里虽然递归方法可以解决斐波那契数列问题，不过随着数字越来越靠后，运行次数将几何倍数增加，严重拖慢运行速度，因此个人认为在这道题有非递归解决可能更方便，不过由于这里介绍递归经典例题我就不详细讲这种方法了，代码奉上给各位有问题我们可以私信或者评论区探讨

int fib(int m)
{
	int ret = 1;
	int a; 
	int b=1;
	while (m > 2)
	{
		m -= 1;
		a = b;
		b = ret;
		ret = a + b;
	}
	return ret;
}

int main()
{
	int m = 0;
	scanf("%d", &m);
	int ret = fib(m);
	printf("%d", ret);
	return 0;
}

---

3、青蛙跳台阶问题

问题背景：

一只青蛙一次可以跳上1级台阶，也可以跳上2 级，，此时该青蛙跳上一个n级的台阶总共有多少种跳法

算法分析：

当只有一级台阶时候，那么就只有跳上去一个方法，因此跳法就是1；

当只有两级台阶时候，那么我们可以先跳一级再跳一级或者直接跳两个，因此跳法就是2；

当有三级及三级以上台阶的时候，我们可以分析一下。题目说一次只能跳一级或者两级台阶，因此那岂不是我们要是求出了跳n-1个台阶跳法和跳n-2个台阶跳法，然后跳n-1个的就只有跳一个的一种方法因此乘以1，同理n-2个的乘以2，就可以求出跳n级的方法。

因此用数学语言表达：

jump(n)=jump(n-1)+jump(n-2)*2

这就对了吗？

答：错

不知道各位在我的分析过程中不知道有没有发现一个漏洞，在我们算n-2个台阶时候，连续跳两次的这个过程与我们算n-1个台阶的时候重复了，因此在这里应该把重复的那次扣除，也就是n-2那次不用乘以2即可

 jump(n)=jump(n-1)+jump(n-2)

到这里我们的分析就算全部分析完了，下面就是代码实现了

备注：同斐波那契数列一样这里用递归的话数字一大，计算机运算时间过慢，各位可以根据上面提供的另一种方法写出这个的另一种方法

欢迎各位评论区留下意见~