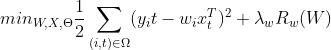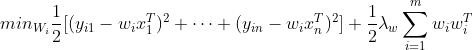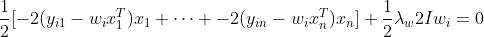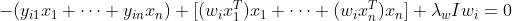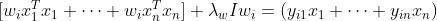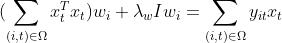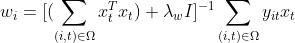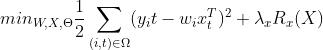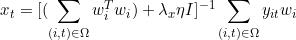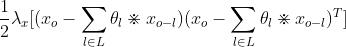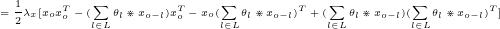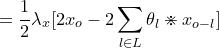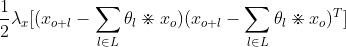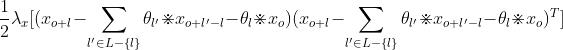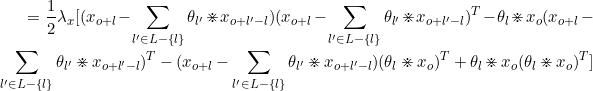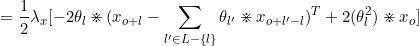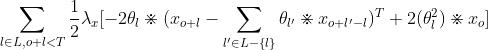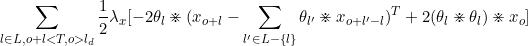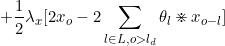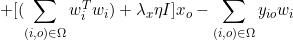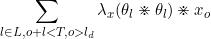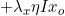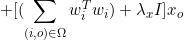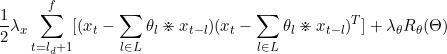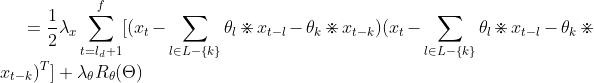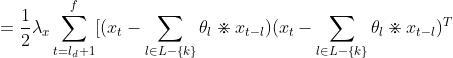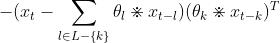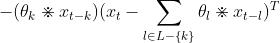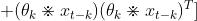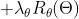TRMF 辅助论文：最小二乘法复现TRMF

Posted 2021-12-09 UQI-LIUWJ

1 目标函数（总）

论文笔记:Temporal Regularized Matrix Factorization forHigh-dimensional Time Series Prediction_UQI-LIUWJ的博客-CSDN博客

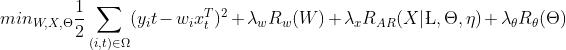
1.1 求解W

我们留下含有W的部分：

 

然后对wi求导

线性代数笔记：标量、向量、矩阵求导_UQI-LIUWJ的博客-CSDN博客

而是一个标量，所以放在xi的左边和右边没有影响

所以

也即：

 对应的代码如下：（假设sparse_mat表示 观测矩阵）

from numpy.linalg import inv as inv
for i in range(dim1):
    #W矩阵的每一行分别计算
    pos0 = np.where(sparse_mat[i, :] != 0)
    #[num_obs] 表示i对应的有示数的数量

    Xt = X[pos0[0], :]
    #[num_obs,rank

    vec0 = sparse_mat[i, pos0[0]] @ Xt
    #sparse_mat[i, pos0[0]] 是一维向量，
    #所以sparse_mat[i, pos0[0]] @ Xt 和 sparse_mat[i, pos0[0]].T @ Xt 是一个意思，
    #输出的都是一个一维向量
    #[rank,1]

    mat0 = inv(Xt.T @ Xt + np.eye(rank))
    #[rank,rank]

    W[i, :] = mat0 @ vec0

 其中：

	vec0 = sparse_mat[i, pos0[0]] @ Xt
	mat0 = inv(Xt.T @ Xt + np.eye(rank))

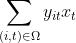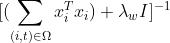1.2 求解X

我们留下含有X的部分

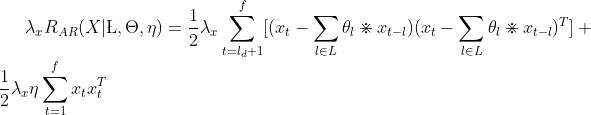
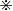表示逐元素乘积 (两个向量a和b，a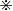b可以用diag(a) b表示）

当t=1~ld的时候，我们没有什么事情，所以此时我们更新X的方式和之前的W差不多

同理，X的更新方式为：

而当t≥ld+1的时候，我们就需要考虑了

对于任意xt（我们令其为xo），他会出现在哪些中呢？

首先 是 

对xo求导，有：

其次，是所有的 

对每一个l，有用的项就是xo相关的项，于是我们可以写成，对每一个l的

对xo求导，有

于是我们可以写成

几部分拼起来，有

=0

=

+

所以xo（o≥ld+1）的更新公式为

[+]

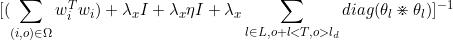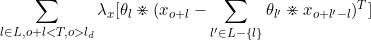
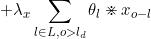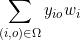3 更新θ

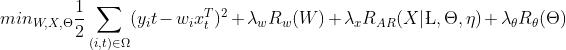
我们留下和θ (θk)有关的部分

关于θk求导

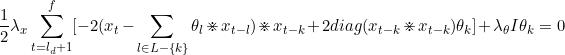
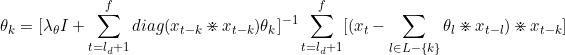
4 总结

x:

t ∈ 1~ld：

t ≥ld+1  [+]