使用贝叶斯优化工具实践XGBoost回归模型调参

Posted 2021-12-08 肖永威

0. 关于调参

0.1. 超参数

在机器学习的上下文中，超参数（hyper parameters）是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，给学习机选择一组最优超参数，以提高学习的性能和效果。

例如深度学习中的学习率、批次大小（batch_size）、优化器（optimizer）等，XGBoost算法中的最大的树深度（max_depth）、子样本比例（subsample）、子节点最小权重和（min_child_weight）等。

0.2. 调参方法

超参数设置通常调参方法如下：

• 随机搜索 （RandomSearch），搜索超参数的值不是固定，是在一定范围内随机的值；
• 网格搜索（GridSearch ），给定超参和取值范围，遍历所有组合得到最优参数。首先你要给定一个先验的取值，不能取得太多，否则组合太多，耗时太长，可以启发式的尝试；
• 贝叶斯优化（Bayesian optimization），采用高斯过程迭代式的寻找最优参数，每次迭代都是在上一次迭代基础上拟合高斯函数上，寻找比上一次迭代更优的参数。

本文主要是分享贝叶斯优化调参方法，其他略。

1. 贝叶斯优化理论

贝叶斯优化是一种逼近思想，当计算非常复杂、迭代次数较高时能起到很好的效果，多用于超参数确定。

贝叶斯优化算法主要包含两个核心部分——概率代理模型（probabilistic surrogate model）和采集函数
(acquisition function)。

• 概率代理模型包含先验概率模型和观测模型：先验概率模$p(f)$；观测模型描述观测数据生成的机
  制，即似然分布$p(D|f)$。更新概率代理模型意味着根据公式 (1)得到包含更多数据信息的后验概率分布
  $p(f|D_i)$。
• 采集函数是根据后验概率分布（高斯过程）构造的，通过最大化采集函数来选择下一个最有 “潜 力”的评估点。同时 ，有效的采集函数能够保证选择的评估点序列使得总损失(loss)最小．损失有 时表示为regret：
  $$r_n=|y^{\ast }-y_n|$$
  或者累计表示为：$$R_i=\sum _{i=1}^n$$其中，$y^{\ast }$表示当前最优解。

掌握贝叶斯优化调参，须要从三个部分讲起：

• 贝叶斯定理
• 高斯过程，用以拟合优化目标函数
• 贝叶斯优化，包括了“开采”和“勘探”，用以花最少的代价找到最优值

1.1. 贝叶斯定理

贝叶斯优化名称的由来是因为参数优化中使用了贝叶斯定理。

$$p(f|D_i)=\frac{p(D_i|f)p(f)}{p(D_i)}(1)$$

其中，$f$表示未知目标函数（或者标识参数模型中的参数）：

• $D_i=(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$表示已观测集合，$x_i$表示决策向量，$y_i=f(x_i)+{\epsilon }_i$表示观测值误差；
• $p(D_i|f)$表示$y$的似然分布；
• $p(f)$表示$f$先验概率分布，对未知目标函数的假设；
• $p(D_i)$表示边际化$f$的边际似然分布或者“证据”，由于该边际似然存在概率密度函数的乘积和积 分，通 常难以得到明确的解析式，该边际似然在贝叶斯优化中主要用于优化超参数(hyper-parameter)；
• $p(f|D_i)$表示$f$的后验概率分布，后验概率分布描述通过己观测数据集对先验进行修正后未知目标函数的置信度。

贝叶斯定理是关于随机事件A和B的条件概率（或边缘概率）的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。

1.2. 高斯过程（Gaussian Process）

高斯过程（GP）全称是高斯分布随机过程，是一个可以被用来表示函数的分布情况的模型。当前，机器学习的常见做法是把函数参数化，然后用产生的参数建模来规避分布表示（如线性回归的权重）。但GP不同，它直接对函数建模生成非参数模型。由此产生的一个突出优势就是它不仅能模拟任何黑盒函数，还能模拟不确定性。这种对不确定性的量化是十分重要的，如当我们被允许请求更多数据时，依靠高斯过程，我们能探索最不可能实现高效训练的数据区域。这也是贝叶斯优化背后的主要思想。

那么高斯分布是如何计算的呢？

假设$f\sim GP(\mu ,K)$，对于$GP$高斯过程，其中$\mu$为均值，$K$为协方差核。所以预测也是服从正态分布的，即有$p(y|x,D)=N(\hat{y},{\hat{\sigma }}^2)$。

当随机变量的维度上升到有限$n$的时候，称之为高维高斯分布，$p(x)=N(\mu ,{\sum }_{n\times n})$。

对于一个$n$维的高斯分布而言，决定它的分布是两个参数：

• $n$维均值向量${\mu }_n$，表示$n$维高斯分布中各个维度随机变量的期望；
• $n\times n$的协方差矩阵${\sum }_{n\times n}$，表示高维分布中，各个维度自身的方差，以及不同维度间的协方差。

核函数(协方差函数)

核函数是一个高斯过程的核心，核函数决定了一个高斯过程的性质。核函数在高斯过程中起生成一个协方差矩阵(相关系数矩阵)来衡量任意两个点之间的“距离”。不同的核函数有不同的衡量方法，得到的高斯过程的性质也不一样。最常用的一个核函数为高斯核函数，也成为径向基函数 RBF。其基本形式如下。

$$K(x_i,x_j)={\sigma }^{2}exp(-\frac{||x_i-x_j|{|}_2^2}{2l^2})$$

其中$\sigma$和$l$是高斯核的超参数。

本文使用的BayesianOptimization的源代码中，高斯过程使用了sklearn.gaussian_process，如下截部分取代码所示。

from sklearn.gaussian_process.kernels import Matern
from sklearn.gaussian_process import GaussianProcessRegressor
......
        self._random_state = ensure_rng(random_state)

        # Data structure containing the function to be optimized, the bounds of
        # its domain, and a record of the evaluations we have done so far
        self._space = TargetSpace(f, pbounds, random_state)

        # queue
        self._queue = Queue()

        # Internal GP regressor
        self._gp = GaussianProcessRegressor(
            kernel=Matern(nu=2.5),
            alpha=1e-6,
            normalize_y=True,
            n_restarts_optimizer=5,
            random_state=self._random_state,
        )

        self._verbose = verbose
        self._bounds_transformer = bounds_transformer
        if self._bounds_transformer:
            self._bounds_transformer.initialize(self._space)

        super(BayesianOptimization, self).__init__(events=DEFAULT_EVENTS)

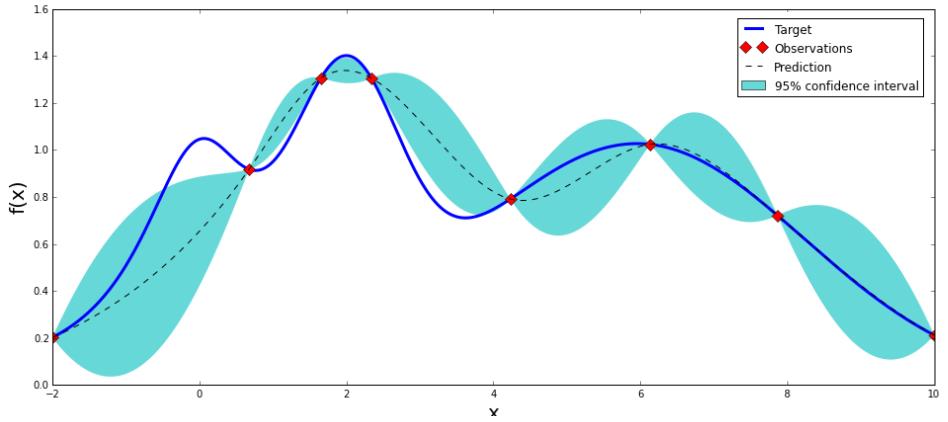
上图是一张高斯分布拟合函数的示意图，可以看到，它只需要九个点，就可以大致拟合出整个函数形状（图片来自：https://github.com/fmfn/BayesianOptimization）

1.3. 贝叶斯优化

参数优化基本思想是基于数据使用贝叶斯定理估计目标函数的后验分布，然后再根据分布选择下一个采样的超参数组合。它充分利用了前一个采样点的信息，其优化的工作方式是通过对目标函数形状的学习，并找到使结果向全局最大提升的参数。

假设一组超参数组合是$X=x_1,以上是关于使用贝叶斯优化工具实践XGBoost回归模型调参的主要内容，如果未能解决你的问题，请参考以下文章$

基于Python贝叶斯优化XGBoost算法调参报错“TypeError: ‘float‘ object is not subscriptable”

随机森林算法及贝叶斯优化调参Python实践

随机森林算法及贝叶斯优化调参Python实践

随机森林算法及贝叶斯优化调参Python实践

基于Python贝叶斯优化XGBoost算法调参报错“TypeError: ‘float‘ object is not subscriptable”

基于Python贝叶斯优化XGBoost算法调参报错“TypeError: ‘float‘ object is not subscriptable”