算法剑指 Offer II 054. 所有大于等于节点的值之和|538|1038(多语言实现)
Posted 二当家的白帽子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法剑指 Offer II 054. 所有大于等于节点的值之和|538|1038(多语言实现)相关的知识,希望对你有一定的参考价值。
非常感谢你阅读本文~
欢迎【👍点赞】【⭐收藏】【📝评论】~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
文章目录
剑指 Offer II 054. 所有大于等于节点的值之和|538. 把二叉搜索树转换为累加树|1038. 把二叉搜索树转换为累加树:
给定一个二叉搜索树,请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
样例 1
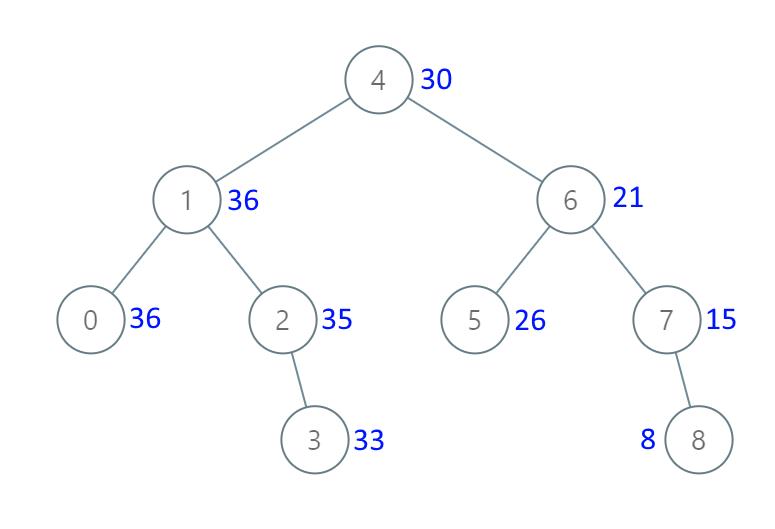
输入:
root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:
[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
样例 2
输入:
root = [0,null,1]
输出:
[1,null,1]
样例 3
输入:
root = [1,0,2]
输出:
[3,3,2]
样例 4
输入:
root = [3,2,4,1]
输出:
[7,9,4,10]
提示
- 树中的节点数介于 0 和 104 之间。
- 每个节点的值介于 -104 和 104 之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
分析
- 这道算法题需要翻译一下,通俗易懂一点。
- 二叉树,大家应该比较熟悉,一般就是正序遍历,中序遍历,后序遍历,然后遍历的过程中进行一些简单的逻辑。
- 二叉搜索树是一种特殊的二叉树,题目已经做了解释。
- 由于要把每个节点的值替换成树中大于或者等于该节点值的所有节点值之和,根据二叉搜索树的特点,其实就是将每个节点的值替换成自己的值累加右子树的值之和。
- 首先这一样需要遍历每个节点,但是按照什么顺序是关键,你会发现常规正序遍历,中序遍历,后序遍历都不顺畅。
- 按照题意来看,显然最好的顺序就是先遍历右子树,然后根节点,接着左子树这样是最顺畅的,仅需要一个变量不断累加节点值,遍历到哪个节点就累加哪个节点的值,然后赋值给这个节点,这正好和中序遍历是反正的,也就是逆中序遍历。
- 遍历这种套娃结构,一般就是递归或者循环(利用栈数据结构),递归相对比较简单,但是受调用栈限制,循环其实就是用栈这样的数据结构模拟了调用栈,本质上差不多,但是调用次数可以更多,因为调用栈的空间一般比较有限,堆空间比起来要大的多,但是实现同样的功能,逻辑上也复杂一些。
- 无论用递归还是用栈数据结构去做循环,都需要与树结构对应的额外内存空间,有一种非常巧妙的遍历方法叫做 Morris遍历 ,可以将非递归遍历中的空间复杂度降为O (1),具体的实现二当家的已经加了详细注释,大家也可以去百科一下,做深入了解。
题解
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode convertBST(TreeNode root) {
int sum = 0;
TreeNode cur = root;
while (cur != null) {
if (cur.right == null) {
// 没有比自己值大的孩子
// 轮到处理自己
sum += cur.val;
cur.val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur.left;
} else {
// 右孩子的最左边,比自己大的最小的孩子
// 也就是自己前边最后一个遍历的节点,下一个就该是自己
TreeNode leftmostOfRight = cur.right;
while (leftmostOfRight.left != null
&& leftmostOfRight.left != cur) {
leftmostOfRight = leftmostOfRight.left;
}
if (leftmostOfRight.left == null) {
// 没有做过关联,说明第一次到这里,关联当前节点,保证遍历完比自己大的最小节点之后可以轮到自己
leftmostOfRight.left = cur;
cur = cur.right;
} else {
// 第二次遍历到这里,说明比自己大的都遍历完了
// 解除关系,还原树结构
leftmostOfRight.left = null;
// 轮到处理自己
sum += cur.val;
cur.val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur.left;
}
}
}
return root;
}
}
c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
struct TreeNode* convertBST(struct TreeNode* root){
int sum = 0;
struct TreeNode *cur = root;
while (cur != NULL) {
if (cur->right == NULL) {
// 没有比自己值大的孩子
// 轮到处理自己
sum += cur->val;
cur->val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur->left;
} else {
// 右孩子的最左边,比自己大的最小的孩子
// 也就是自己前边最后一个遍历的节点,下一个就该是自己
struct TreeNode *leftmostOfRight = cur->right;
while (leftmostOfRight->left != NULL
&& leftmostOfRight->left != cur) {
leftmostOfRight = leftmostOfRight->left;
}
if (leftmostOfRight->left == NULL) {
// 没有做过关联,说明第一次到这里,关联当前节点,保证遍历完比自己大的最小节点之后可以轮到自己
leftmostOfRight->left = cur;
cur = cur->right;
} else {
// 第二次遍历到这里,说明比自己大的都遍历完了
// 解除关系,还原树结构
leftmostOfRight->left = NULL;
// 轮到处理自己
sum += cur->val;
cur->val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur->left;
}
}
}
return root;
}
c++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
int sum = 0;
TreeNode *cur = root;
while (cur != nullptr) {
if (cur->right == nullptr) {
// 没有比自己值大的孩子
// 轮到处理自己
sum += cur->val;
cur->val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur->left;
} else {
// 右孩子的最左边,比自己大的最小的孩子
// 也就是自己前边最后一个遍历的节点,下一个就该是自己
TreeNode *leftmostOfRight = cur->right;
while (leftmostOfRight->left != nullptr
&& leftmostOfRight->left != cur) {
leftmostOfRight = leftmostOfRight->left;
}
if (leftmostOfRight->left == nullptr) {
// 没有做过关联,说明第一次到这里,关联当前节点,保证遍历完比自己大的最小节点之后可以轮到自己
leftmostOfRight->left = cur;
cur = cur->right;
} else {
// 第二次遍历到这里,说明比自己大的都遍历完了
// 解除关系,还原树结构
leftmostOfRight->left = nullptr;
// 轮到处理自己
sum += cur->val;
cur->val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur->left;
}
}
}
return root;
}
};
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
total = 0
cur = root
while cur:
if not cur.right:
# 没有比自己值大的孩子
# 轮到处理自己
total += cur.val
cur.val = total
# 自己也遍历完了,所以该遍历比自己小的
cur = cur.left
else:
# 右孩子的最左边,比自己大的最小的孩子
# 也就是自己前边最后一个遍历的节点,下一个就该是自己
leftmostOfRight = cur.right
while leftmostOfRight.left and leftmostOfRight.left != cur:
leftmostOfRight = leftmostOfRight.left
if not leftmostOfRight.left:
# 没有做过关联,说明第一次到这里,关联当前节点,保证遍历完比自己大的最小节点之后可以轮到自己
leftmostOfRight.left = cur
cur = cur.right
else:
# 第二次遍历到这里,说明比自己大的都遍历完了
# 解除关系,还原树结构
leftmostOfRight.left = None
# 轮到处理自己
total += cur.val
cur.val = total
# 自己也遍历完了,所以该遍历比自己小的
cur = cur.left
return root
go
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func convertBST(root *TreeNode) *TreeNode {
sum := 0
cur := root
for cur != nil {
if cur.Right == nil {
// 没有比自己值大的孩子
// 轮到处理自己
sum += cur.Val
cur.Val = sum
// 自己也遍历完了,所以该遍历比自己小的
cur = cur.Left
} else {
// 右孩子的最左边,比自己大的最小的孩子
// 也就是自己前边最后一个遍历的节点,下一个就该是自己
leftmostOfRight := cur.Right
for leftmostOfRight.Left != nil && leftmostOfRight.Left != cur {
leftmostOfRight = leftmostOfRight.Left
}
if leftmostOfRight.Left == nil {
// 没有做过关联,说明第一次到这里,关联当前节点,保证遍历完比自己大的最小节点之后可以轮到自己
leftmostOfRight.Left = cur
cur = cur.Right
} else {
// 第二次遍历到这里,说明比自己大的都遍历完了
// 解除关系,还原树结构
leftmostOfRight.Left = nil
// 轮到处理自己
sum += cur.Val
cur.Val = sum
// 自己也遍历完了,所以该遍历比自己小的
cur = cur.Left
}
}
}
return root
}
rust
// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
pub fn convert_bst(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
let mut sum = 0;
let mut cur = root.clone();
while cur.is_some() {
if cur.as_ref().unwrap().borrow().right.is_none() {
// 没有比自己值大的孩子
// 轮到处理自己
sum += cur.as_ref().unwrap().borrow().val;
cur.as_ref().unwrap().borrow_mut().val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur.unwrap().borrow().left.clone();
} else {
// 右孩子的最左边,比自己大的最小的孩子
// 也就是自己前边最后一个遍历的节点,下一个就该是自己
let mut leftmostOfRight = cur.as_ref().unwrap().borrow().right.clone();
while leftmostOfRight.as_ref().unwrap().borrow().left.is_some()
&& leftmostOfRight.as_ref().unwrap().borrow().left != cur {
leftmostOfRight = leftmostOfRight.unwrap().borrow().left.clone();
}
if leftmostOfRight.as_ref().unwrap().borrow().left.is_none() {
// 没有做过关联,说明第一次到这里,关联当前节点,保证遍历完比自己大的最小节点之后可以轮到自己
leftmostOfRight.unwrap().borrow_mut().left = cur.clone();
cur = cur.unwrap().borrow().right.clone();
} else {
// 第二次遍历到这里,说明比自己大的都遍历完了
// 解除关系,还原树结构
leftmostOfRight.unwrap().borrow_mut().left = Option::None;
// 轮到处理自己
sum += cur.as_ref().unwrap().borrow().val;
cur.as_ref().unwrap().borrow_mut().val = sum;
// 自己也遍历完了,所以该遍历比自己小的
cur = cur.unwrap().borrow().left.clone();
}
}
}
root
}
}
原题传送门:https://leetcode-cn.com/problems/w6cpku/
原题传送门:https://leetcode-cn.com/problems/convert-bst-to-greater-tree/
原题传送门:https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/
以上是关于算法剑指 Offer II 054. 所有大于等于节点的值之和|538|1038(多语言实现)的主要内容,如果未能解决你的问题,请参考以下文章
leetcode剑指 Offer II 008. 和大于等于 target 的最短子数组
leetcode剑指 Offer II 008. 和大于等于 target 的最短子数组
leetcode剑指 Offer II 008. 和大于等于 target 的最短子数组