networkx图论Prim Algorithm最小生成树，Python

Posted 2021-12-06 zhangphil

借助networkx提供的节点、边、图绘制便捷功能，自己写了一个Prim逻辑实现，练手。

最小生成树现实中场景：比如大城市多个地点之间修建连通的公路，如何选择连接的点，才使得建造代价最小、且能够连通所有城市地点。

Prim Algorithm核心是：迭代寻找最小权边的点，接入图。

把图中的节点分为U，V两部分，可以先把V装满图中的点,V=[v2,v3,v4,v5,,,vn]。算法启动时候，U=[]为空，任取一点假设是v1装入U，U=[v1]，然后将V中所有与U中点邻接的点形成的边，取权最小的，把点从V中移除放入U。依次迭代，注意，越往后，U中点越多，要计算所有U中点和V中点邻接的边，取最小的权。

import sys

import networkx as nx
import matplotlib.pyplot as plt


# 这里实现的代码里面有两个潜在的遗留问题未解决：
# 1，选边时候，对有可能形成的环未做处理。
# 2，加点时候，如果出现多条相同权边的选择，算法是否会稳定？
def prim(G):
    my_edge_bfs = list(nx.edge_bfs(G=G, source=G.nodes))
    print('所有联通子路径', my_edge_bfs)
    print('所有边', G.edges())
    print('所有边权', G.edges(data=True))

    nodes = list(G.nodes)

    U = [nodes[0]]
    V = nodes[1:]

    min_edges = []
    while True:
        if len(V) == 0:
            break

        print('-----')
        print('节点划分', U, V)

        node_visit = []

        for vn in V:
            for un in U:
                for med in my_edge_bfs:
                    if (un in med) and (vn in med):
                        ws = get_edge_weight(med, G)
                        print('存在通路->', med, ws)
                        node_visit.append((med, ws))

        print('访问节点放入列表', node_visit)
        min_edge = find_min_edge(node_visit)
        print('通路的最小权边', min_edge)
        min_edges.append(min_edge)

        for e in min_edge[0]:
            if e not in U:
                U.append(e)

        # 找出两个list的交集
        c = list(set(min_edge[0]).intersection(set(V)))
        print('V中应该删掉的节点:', c[0])
        V.remove(c[0])

        print('*最小生成树=', U)
        print('*最小生成树的边=', min_edges)

    return min_edges


def my_graph():
    # 构造一个有权边的无向图，然后找出最小生成树
    G = nx.Graph()  # 无向图

    nodes = ['a', 'b', 'c', 'd', 'e', 'f']
    G.add_nodes_from(nodes)

    G.add_edges_from([('a', 'b', {'weight': 6}),
                      ('a', 'c', {'weight': 1}),
                      ('a', 'd', {'weight': 5}),
                      ('b', 'c', {'weight': 5}),
                      ('c', 'd', {'weight': 5}),
                      ('b', 'e', {'weight': 3}),
                      ('c', 'e', {'weight': 6}),
                      ('e', 'f', {'weight': 6}),
                      ('c', 'f', {'weight': 4}),
                      ('d', 'f', {'weight': 2})])

    pos = nx.spring_layout(G)
    nx.draw(G, pos,
            node_color='green',
            node_size=500,
            font_size=10,
            font_color='black',
            edge_color='gray',
            width=1,
            alpha=0.5,
            with_labels=True)

    my_edge_labels = nx.get_edge_attributes(G, 'weight')
    nx.draw_networkx_edge_labels(G, pos, edge_labels=my_edge_labels)

    min_edges = prim(G)

    edge_list = []
    for edge in min_edges:
        edge_list.append(edge[0])

    # 把最小生成树的边着色加粗重新描边
    nx.draw_networkx_edges(G, pos,
                           edgelist=edge_list,
                           width=8,
                           alpha=0.5,
                           edge_color="r")

    plt.show()


# 传入一个边，找到该边对应的权
# 这里没有解决如果若干条边同时具有相同的权值，应该返回一个列表
def get_edge_weight(edge, G):
    WEIGHT = sys.maxsize

    weights = nx.get_edge_attributes(G, 'weight')
    for e in G.edges():
        if e == edge:
            w = weights.get(e)
            WEIGHT = w

    return WEIGHT


# 这里没有解决如果若干条边同时具有相同的权值问题，应该返回一个列表，装入所有相同值的边
def find_min_edge(edges):
    w_val = []
    for e in edges:
        w_val.append(e[1])
    min_w = min(w_val)
    i = w_val.index(min_w)
    return edges[i]


if __name__ == '__main__':
    my_graph()

生成的最小生成树图，红色权边即为：

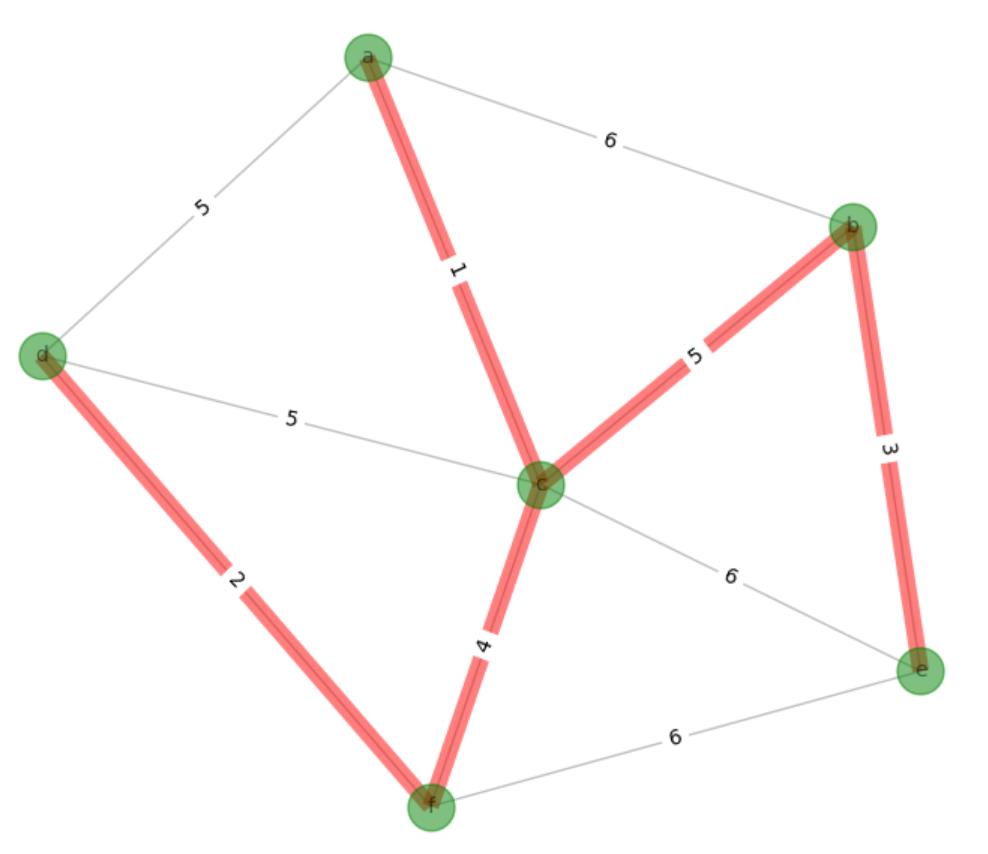
运行日志：

所有联通子路径 [('a', 'b'), ('a', 'c'), ('a', 'd'), ('b', 'c'), ('b', 'e'), ('c', 'd'), ('c', 'e'), ('c', 'f'), ('d', 'f'), ('e', 'f')]
所有边 [('a', 'b'), ('a', 'c'), ('a', 'd'), ('b', 'c'), ('b', 'e'), ('c', 'd'), ('c', 'e'), ('c', 'f'), ('d', 'f'), ('e', 'f')]
所有边权 [('a', 'b', {'weight': 6}), ('a', 'c', {'weight': 1}), ('a', 'd', {'weight': 5}), ('b', 'c', {'weight': 5}), ('b', 'e', {'weight': 3}), ('c', 'd', {'weight': 5}), ('c', 'e', {'weight': 6}), ('c', 'f', {'weight': 4}), ('d', 'f', {'weight': 2}), ('e', 'f', {'weight': 6})]
-----
节点划分 ['a'] ['b', 'c', 'd', 'e', 'f']
存在通路-> ('a', 'b') 6
存在通路-> ('a', 'c') 1
存在通路-> ('a', 'd') 5
访问节点放入列表 [(('a', 'b'), 6), (('a', 'c'), 1), (('a', 'd'), 5)]
通路的最小权边 (('a', 'c'), 1)
V中应该删掉的节点: c
*最小生成树= ['a', 'c']
*最小生成树的边= [(('a', 'c'), 1)]
-----
节点划分 ['a', 'c'] ['b', 'd', 'e', 'f']
存在通路-> ('a', 'b') 6
存在通路-> ('b', 'c') 5
存在通路-> ('a', 'd') 5
存在通路-> ('c', 'd') 5
存在通路-> ('c', 'e') 6
存在通路-> ('c', 'f') 4
访问节点放入列表 [(('a', 'b'), 6), (('b', 'c'), 5), (('a', 'd'), 5), (('c', 'd'), 5), (('c', 'e'), 6), (('c', 'f'), 4)]
通路的最小权边 (('c', 'f'), 4)
V中应该删掉的节点: f
*最小生成树= ['a', 'c', 'f']
*最小生成树的边= [(('a', 'c'), 1), (('c', 'f'), 4)]
-----
节点划分 ['a', 'c', 'f'] ['b', 'd', 'e']
存在通路-> ('a', 'b') 6
存在通路-> ('b', 'c') 5
存在通路-> ('a', 'd') 5
存在通路-> ('c', 'd') 5
存在通路-> ('d', 'f') 2
存在通路-> ('c', 'e') 6
存在通路-> ('e', 'f') 6
访问节点放入列表 [(('a', 'b'), 6), (('b', 'c'), 5), (('a', 'd'), 5), (('c', 'd'), 5), (('d', 'f'), 2), (('c', 'e'), 6), (('e', 'f'), 6)]
通路的最小权边 (('d', 'f'), 2)
V中应该删掉的节点: d
*最小生成树= ['a', 'c', 'f', 'd']
*最小生成树的边= [(('a', 'c'), 1), (('c', 'f'), 4), (('d', 'f'), 2)]
-----
节点划分 ['a', 'c', 'f', 'd'] ['b', 'e']
存在通路-> ('a', 'b') 6
存在通路-> ('b', 'c') 5
存在通路-> ('c', 'e') 6
存在通路-> ('e', 'f') 6
访问节点放入列表 [(('a', 'b'), 6), (('b', 'c'), 5), (('c', 'e'), 6), (('e', 'f'), 6)]
通路的最小权边 (('b', 'c'), 5)
V中应该删掉的节点: b
*最小生成树= ['a', 'c', 'f', 'd', 'b']
*最小生成树的边= [(('a', 'c'), 1), (('c', 'f'), 4), (('d', 'f'), 2), (('b', 'c'), 5)]
-----
节点划分 ['a', 'c', 'f', 'd', 'b'] ['e']
存在通路-> ('c', 'e') 6
存在通路-> ('e', 'f') 6
存在通路-> ('b', 'e') 3
访问节点放入列表 [(('c', 'e'), 6), (('e', 'f'), 6), (('b', 'e'), 3)]
通路的最小权边 (('b', 'e'), 3)
V中应该删掉的节点: e
*最小生成树= ['a', 'c', 'f', 'd', 'b', 'e']
*最小生成树的边= [(('a', 'c'), 1), (('c', 'f'), 4), (('d', 'f'), 2), (('b', 'c'), 5), (('b', 'e'), 3)]