图论Dijkstra Algorithm在2D空间平面网格节点图选择最短路径,networkx,Python
Posted zhangphil
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图论Dijkstra Algorithm在2D空间平面网格节点图选择最短路径,networkx,Python相关的知识,希望对你有一定的参考价值。
图论Dijkstra Algorithm在2D空间平面网格节点图选择最短路径,networkx,Python
(1)Dijkstra Algorithm算法结束后,在代码生成的二维网格图中所有节点的权值即为出发点(源点)到当前节点的最短路径。本例中网格图中所有邻接边权值为1。
(2)通过每个节点中保存的parent指针一路逆行往上迭代查找,直到出发点(源点),即为出发点到当前节点的最短路径。parent指针指向了到当前节点的最短路径父节点。
(3)Dijkstra Algorithm寻路结束后,出发点(源点)到所有可达点的最短距离确定(weight值即为最短路径值)。从中可以得到启发,比如多人对战游戏,一张地图中同一时刻多人需要知道到达某汇聚点的路径,那么这种算法应用场景,Dijkstra Algorithm就很适合(反而A*算法在这种应用场景不适合,因为A*算法确定的是一个出发点到一个终点的路线。如果是N个人,就需要N次运行A*算法,才能为N个人完成选路),而Dijkstra Algorithm只需一次寻路,就完成所有地图中的点(某个点代表某个人的位置)到某个源点的最短距离。
(4)Dijkstra Algorithm在本例中作为一种广度优先搜索寻找最短路径,在每个节点中加入的parent指针,将其形成一定程度具有深度的寻路思想。这种思想在寻路算法中很普遍,在广度和深度的搜索过程中,通过埋入一个指针parent,可以快速找到出发点到源点的最短路径。
import random
import networkx as nx
import matplotlib.pyplot as plt
WALKABLE = 'walkable'
PARENT = 'parent'
WEIGHT = 'weight'
def my_graph():
M = 7
N = 9
G = nx.grid_2d_graph(m=M, n=N)
pos = nx.spring_layout(G, iterations=100)
nx.draw_networkx(G, pos=pos,
# labels=labels, #labels = dict(((i, j), 'Phil') for i, j in G.nodes())
font_size=8,
font_color='white',
node_color='green',
node_size=500,
width=1)
START = (1, 1)
GOAL = (M - 1 - 1, N - 1 - 1)
# 0,随机生成障碍物点
# 1,精心挑选的障碍物构成陷阱
OBSTACLE_MODE = 0
road_closed_nodes = []
if OBSTACLE_MODE == 0:
obstacle_number = 20 # 障碍物(断点、不可达点)数量
road_closed_nodes = obstacle_nodes(G, START, GOAL, obstacle_number, M, N)
elif OBSTACLE_MODE == 1:
road_closed_nodes = dummy_nodes(G)
nx.draw_networkx_nodes(
G, pos,
nodelist=road_closed_nodes,
node_size=500,
node_color="red",
node_shape="x",
# alpha=0.3,
label='x'
)
dijkstra_find_path(G, START, G.number_of_nodes() - len(road_closed_nodes))
print('G.nodes(data=True) 更新节点权值后', G.nodes(data=True))
path = find_path_by_parent(G, START, GOAL)
print('path', path)
nx.draw_networkx_nodes(
G, pos,
nodelist=path,
node_size=400,
node_color="red",
node_shape='o',
# alpha=0.3,
# label='NO'
)
path_edges = []
for i in range(len(path)):
if (i + 1) == len(path):
break
path_edges.append((path[i], path[i + 1]))
print('path_edges', path_edges)
# 把path着色加粗重新描边
nx.draw_networkx_edges(G, pos,
edgelist=path_edges,
width=8,
alpha=0.5,
edge_color="r")
plt.axis('off')
plt.show()
def dijkstra_find_path(G, START, valid_node_number):
# 设置所有节点的权值为无穷大
for n in G.nodes():
G.nodes[n][WEIGHT] = float('inf')
# 更新出发节点权重为0
G.nodes[START][WEIGHT] = 0
print('G.nodes(data=True)', G.nodes(data=True))
print('起点', START)
close_list = []
vertex = START # 顶点
while True:
print('-----')
if len(close_list) == valid_node_number:
print('搜索完毕')
break
update_weight_from_node(G, vertex, close_list)
min_node = find_min_nodes(G, vertex, close_list)
vertex = min_node[0]
close_list.append(vertex)
def update_weight_from_node(G, cur_node, close_list):
cur_node_weight = G.nodes[cur_node][WEIGHT]
neighbors = nx.neighbors(G, cur_node)
for child in neighbors:
try:
walkable = G.nodes[child][WALKABLE]
except:
walkable = True
if (child in close_list) or (not walkable):
continue
edge_weight = 1 # 在本例的2D平面图中,邻接的边权都是1
child_node_weight = G.nodes[child][WEIGHT]
sum_weight = cur_node_weight + edge_weight
if sum_weight < child_node_weight:
G.nodes[child][WEIGHT] = sum_weight
G.nodes[child][PARENT] = cur_node
print('更新节点权值', cur_node, '->', child, '新权值为:', sum_weight)
def find_min_nodes(G, vertex, close_list):
node_list = []
for node in G.nodes(data=True):
try:
walkable = node[1][WALKABLE]
except:
walkable = True
if walkable and (node[0] not in close_list) and (node[0] != vertex):
node_list.append(node)
min_node = min(node_list, key=lambda x: x[1][WEIGHT])
print(vertex, '最小节点', min_node)
return min_node
def find_path_by_parent(G, START, GOAL):
t = GOAL
path = [t]
is_find = False
while not is_find:
for n in G.nodes(data=True):
if n[0] == t:
parent = n[1][PARENT]
path.append(parent)
if parent == START:
is_find = True
break
t = parent
list.reverse(path)
return path
# 障碍物点
def obstacle_nodes(G, START, GOAL, obstacle, M, N):
road_closed_nodes = []
for i in range(obstacle):
n = (random.randint(0, M - 1), random.randint(0, N - 1))
if n == START or n == GOAL:
continue
if n in road_closed_nodes:
continue
G.nodes[n][WALKABLE] = False
road_closed_nodes.append(n)
return road_closed_nodes
def dummy_nodes(G):
fun_nodes = []
n0 = (1, 2)
G.nodes[n0][WALKABLE] = False
fun_nodes.append(n0)
n1 = (1, 3)
G.nodes[n1][WALKABLE] = False
fun_nodes.append(n1)
n2 = (1, 4)
G.nodes[n2][WALKABLE] = False
fun_nodes.append(n2)
n3 = (1, 5)
G.nodes[n3][WALKABLE] = False
fun_nodes.append(n3)
n4 = (1, 6)
G.nodes[n4][WALKABLE] = False
fun_nodes.append(n4)
n5 = (2, 6)
G.nodes[n5][WALKABLE] = False
fun_nodes.append(n5)
n6 = (3, 6)
G.nodes[n6][WALKABLE] = False
fun_nodes.append(n6)
n7 = (4, 6)
G.nodes[n7][WALKABLE] = False
fun_nodes.append(n7)
n8 = (5, 6)
G.nodes[n8][WALKABLE] = False
fun_nodes.append(n8)
n9 = (5, 5)
G.nodes[n9][WALKABLE] = False
fun_nodes.append(n9)
n10 = (5, 4)
G.nodes[n10][WALKABLE] = False
fun_nodes.append(n10)
n11 = (5, 3)
G.nodes[n11][WALKABLE] = False
fun_nodes.append(n11)
n12 = (5, 2)
G.nodes[n12][WALKABLE] = False
fun_nodes.append(n12)
return fun_nodes
if __name__ == '__main__':
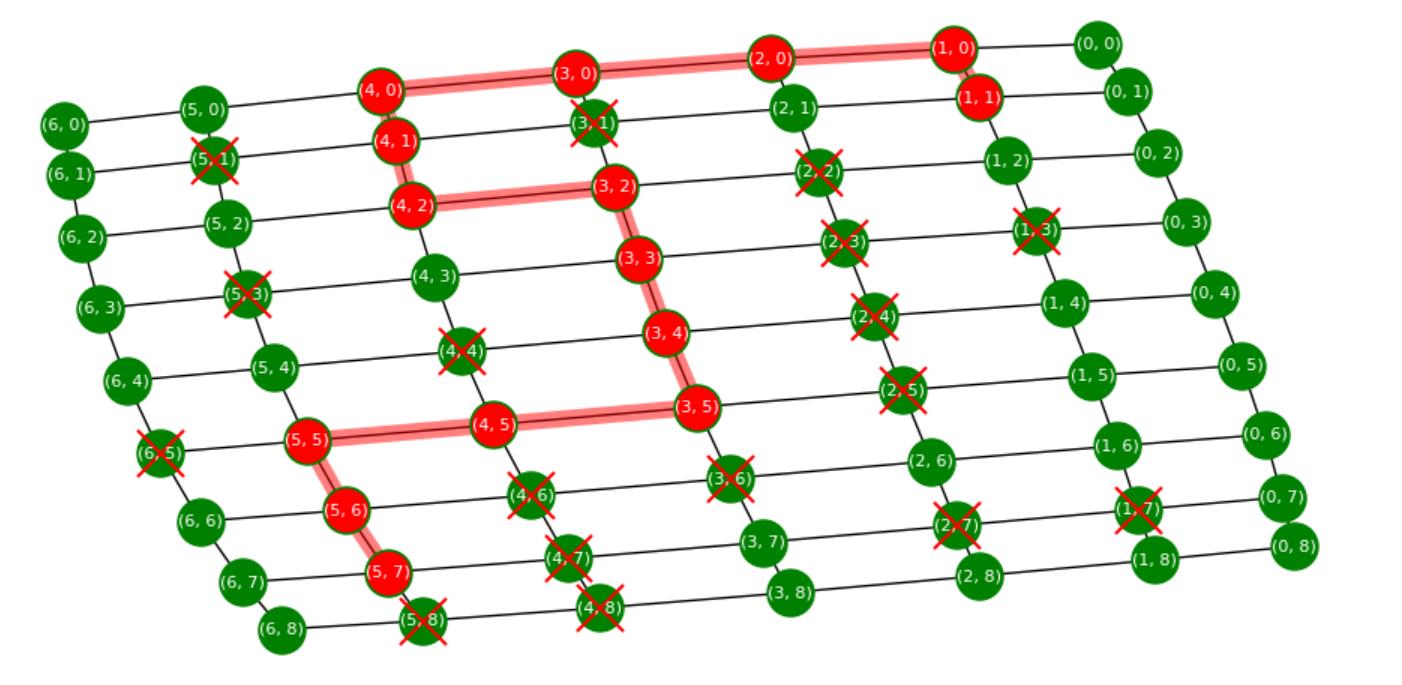
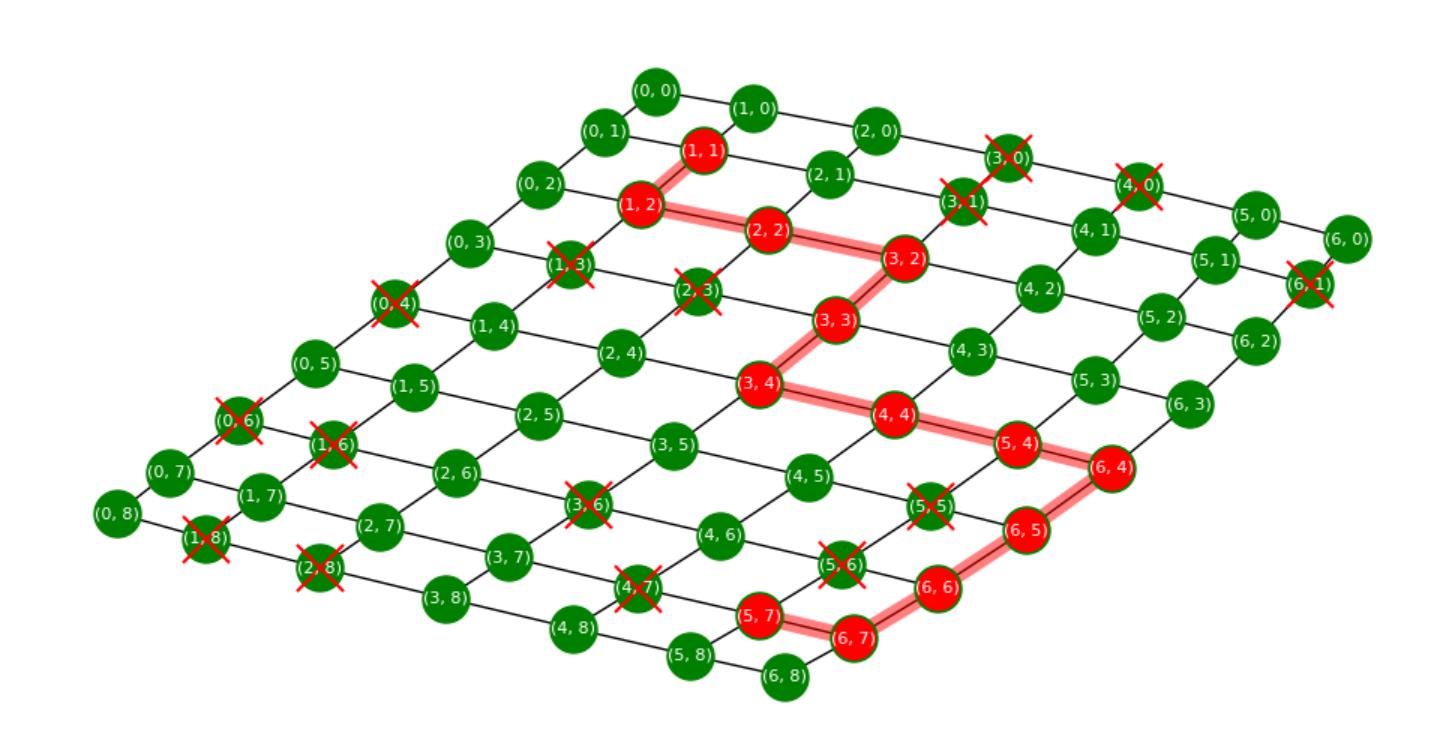
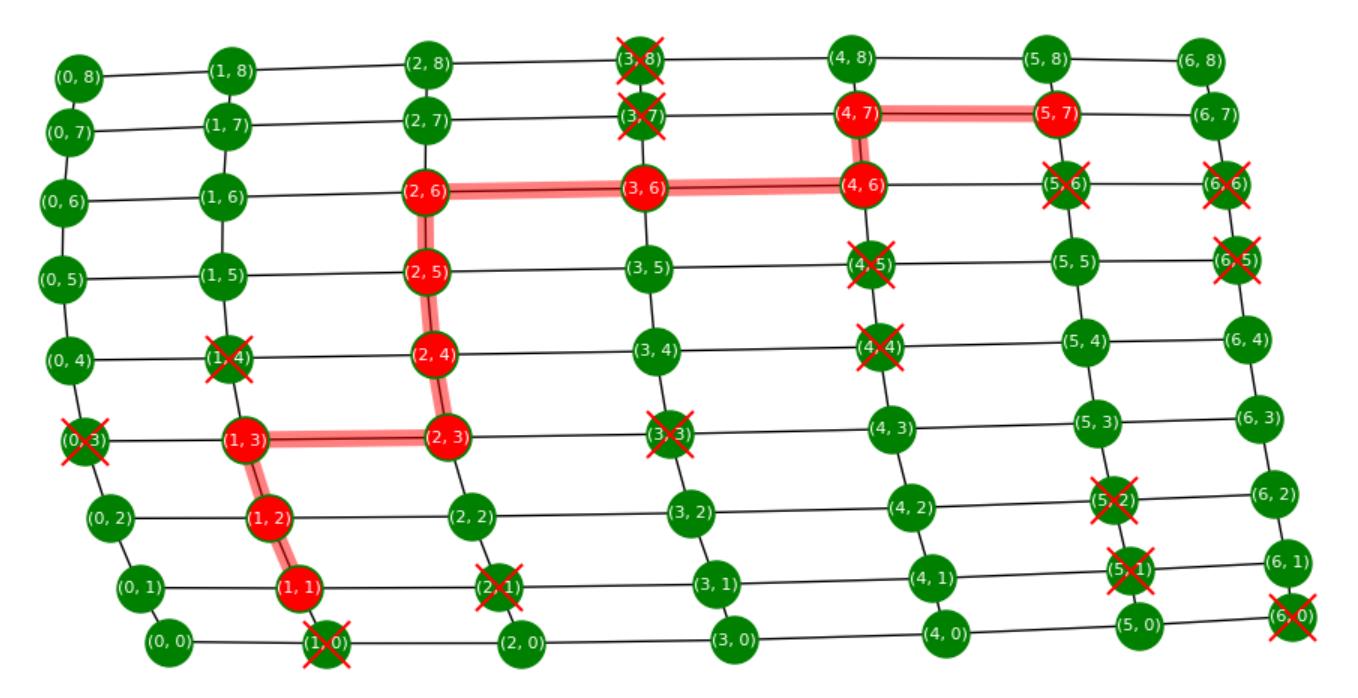
my_graph()运行几轮后的选路截图:
当把障碍物模式切换为1,即特意挑选一批点围成一个围墙,同时把出发点改为(2,2),看看算法的表现:
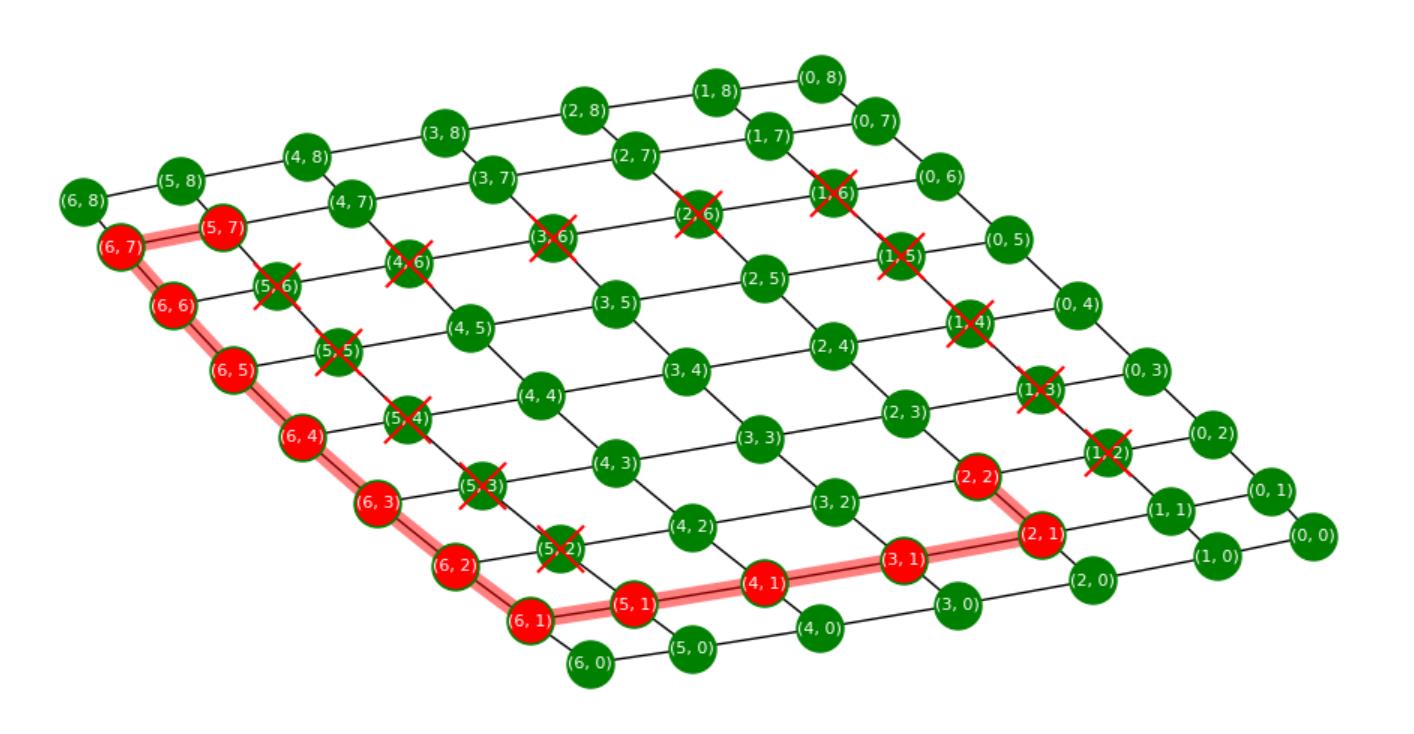
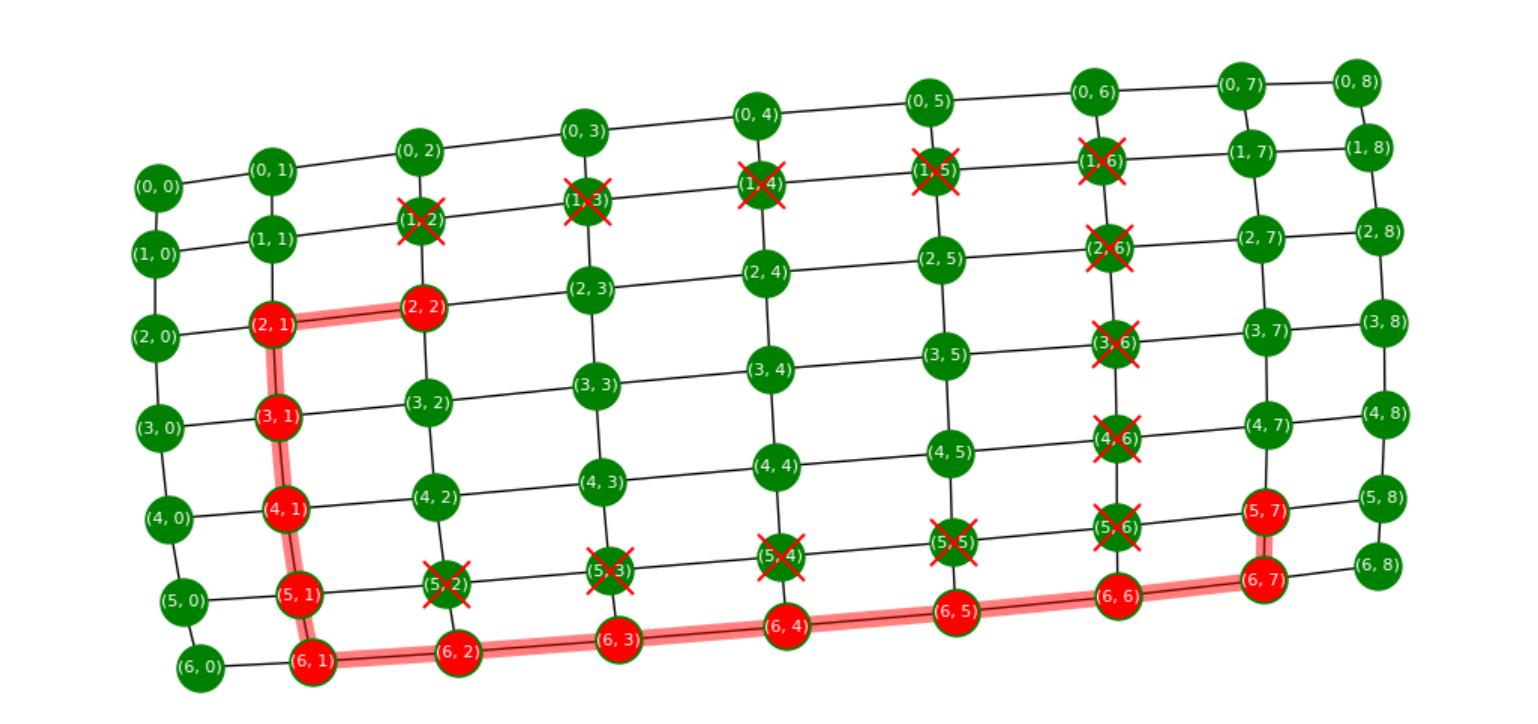
算法聪明的规避了围墙,没有跳进凹形陷阱。
以上是关于图论Dijkstra Algorithm在2D空间平面网格节点图选择最短路径,networkx,Python的主要内容,如果未能解决你的问题,请参考以下文章
networkx图论最短路径Dijkstra Algorithm,Python
networkx图论Dijkstra Algorithm最短路径实现,Python
networkx图论贝尔曼-福特Bellman Ford Algorithm最短路径,Python
图论DFS(Depth First Search)Algorithm深度优先搜索遍历空间平面图选择路径,networkx,Python
图论DFS(Depth First Search)Algorithm深度优先搜索遍历空间平面图选择路径,networkx,Python
图论BFS(Breath First Search)Algorithm广度优先搜索遍历空间平面网格图路径选择,networkx,Python