P1616 疯狂的采药 完全背包模型

Posted 2021-12-05 幽殇默

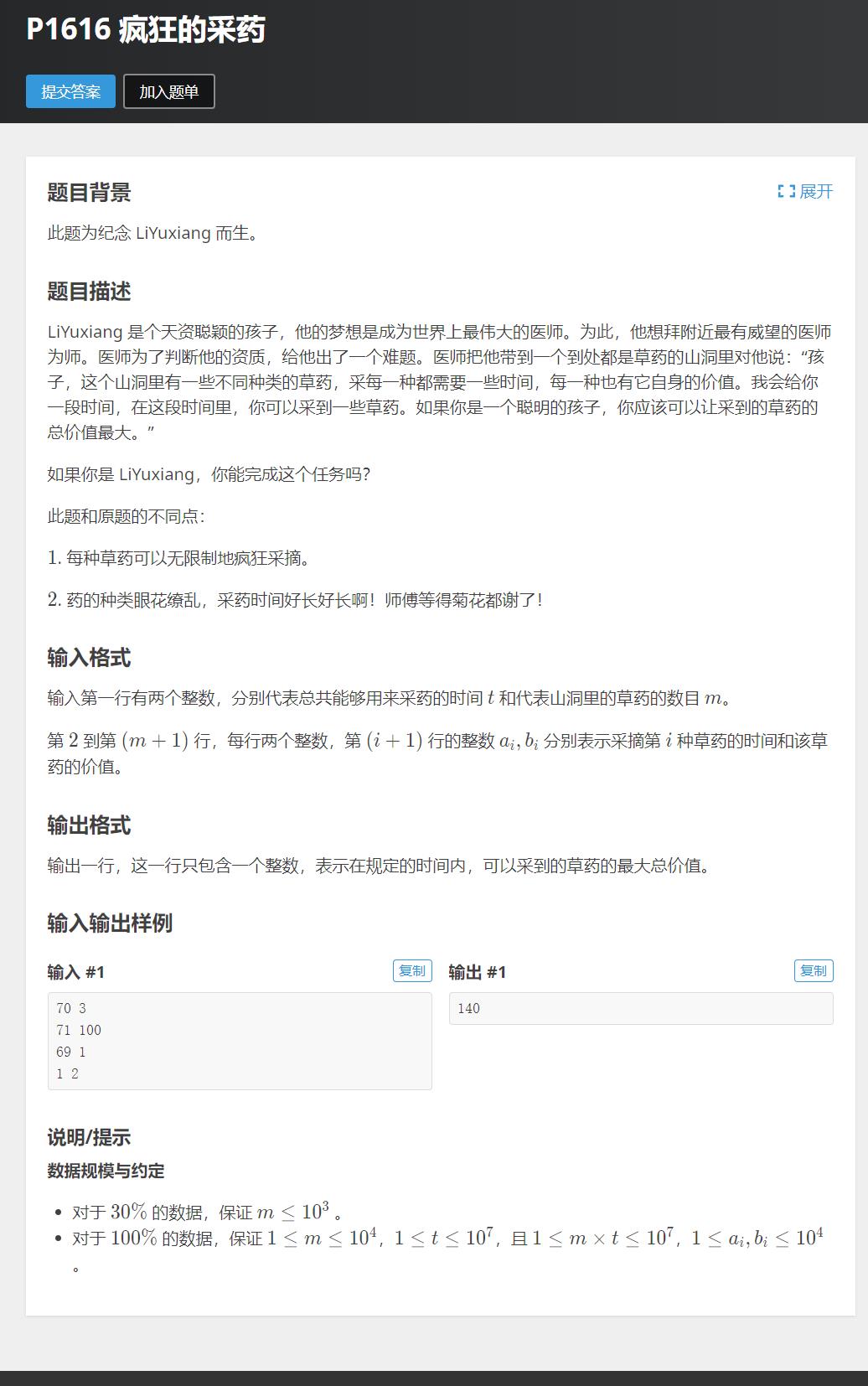
https://www.luogu.com.cn/problem/P1616
这个是典型的完全背包的模型。和01背包不同的是每个物品可以无限选择。
状态表示: f[i][j] 表示从前i个物品中选，总体积不超过j的最大价值
对于f[i][j]状态划分:

• 不选第i件物品f[i][j]=f[i-1][j]
• 选第i件物品
  • 选1件第i件物品f[i-1][j-1*v[i]]+1*w[i]
  • 选2件第i件物品f[i-1][j-2*v[i]]+2*w[i]
  • 选3件第i件物品f[i-1][j-3*v[i]]+3*w[i]
  • …选k件第i件物品f[i-1][j-k*v[i]]+k*w[i]

由上分析，代码不难写出：

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int f[N][N],v[N],w[N],n,m; 
int main(void)
{
	cin>>m>>n;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			for(int k=0;k*v[i]<=m;k++)
			{
				if(k*v[i]<=j) f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
			}
		}
	}
	cout<<f[n][m]<<endl;
} 

当然上面这个代码是不可行的，因为三层循环，太暴力了，得优化。

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w ,  f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max(            f[i-1,j-v]   ,  f[i-1,j-2*v] + w , f[i-1,j-2*v]+2*w , .....)
由上两式，可得出如下递推关系： 
                        f[i][j]=max(f[i-1][j] , f[i,j-v]+w) 

故代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int f[N][N],v[N],w[N],n,m; 
int main(void)
{
	cin>>m>>n;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			f[i][j]=f[i-1][j];
			if(j>=v[i]) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
		}
	}
	cout<<f[n][m]<<endl;
} 

上面的代码会爆内存，故我们得优化成一维的。

#include<bits/stdc++.h>
using namespace std;
const int N=1e7+10;
long long int f[N],v[N],w[N],n,m; 
int main(void)
{
	cin>>m>>n;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
	{
		for(int j=v[i];j<=m;j++)
		{
			f[j]=max(f[j],f[j-v[i]]+w[i]);
		}
	}
	cout<<f[m]<<endl;
}