算法零基础学习leetcode 231326324题解

Posted 2021-12-04 过气老学长

目录

• 2的幂
• • 问题描述
  • 解决方案一：换底公式
  • 解决方案二：位运算
  • 解决方案三：判断是否为最大幂值的约数
• 3的幂
• • 问题描述
  • 解决方案：判断是否为最大幂值的约数
• 4的幂
• • 问题描述
  • 解决方案一：暴力求解
  • 解决方案二：位运算

2的幂

问题描述

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。
如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。
-2³¹ <= n <= 2³¹ - 1

解决方案一：换底公式

class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n == 0)  return false;
       int x = (int)(Math.log(n)/Math.log(2));
       if(Math.pow(2,x) == n){
           return true;
       }else{
           return false;
       }
    }
}

解决方案二：位运算

2的幂的二进制结果有且仅有一个1，所以，可以使用n & (n - 1)公式将这个1给去除，最终的结果为0。

序号	2x	二进制表示
0	1	0001
1	2	0010
2	4	0000 0100
3	8	0000 1000
4	16	0001 0000

class Solution {
    public boolean isPowerOfTwo(int n) {
        return n > 0 && (n & (n -1)) == 0;
    }
}

解决方案三：判断是否为最大幂值的约数

因为规定了n的有效范围是-2^31^~2^31^-1，所以，幂的最大值是2³⁰ = 1073741824。只要n是这个值的约数，那么这个值一定是2的幂。

class Solution {
    public boolean isPowerOfTwo(int n) {
    		int max = 1073741824
        return n > 0 && max % n == 0;
    }
}

3的幂

问题描述

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。
整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x
-2³¹ <= n <= 2³¹ - 1

解决方案：判断是否为最大幂值的约数

class Solution {
    public boolean isPowerOfThree(int n) {
        return n>0 && 1162261467 % n == 0;	//1162261467是在n范围内的最大幂值
    }
}

4的幂

问题描述

给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true ；否则，返回 false 。
整数 n 是 4 的幂次方需满足：存在整数 x 使得 n == 4x
-2³¹ <= n <= 2³¹ - 1

解决方案一：暴力求解

如果n是4的幂，那么不断地对n做取余和整除运算，最终得到的结果都是1。

class Solution {
    public boolean isPowerOfFour(int n) {
        if(n <= 0){
            return false;
        }
        while(n % 4 == 0){
            n /= 4;
        }

        return n == 1;
    }
}

解决方案二：位运算

和2^x一样，4^x的二进制表示同样只有一个1。所以，可以使用n & (n - 1)进行位运算。

return n > 0 && (n & (n - 1)) == 0;

但是，仅仅这样无法得到正确的结果——因为当n = 2^x且n ≠ 4^x时，返回的结果仍然是true

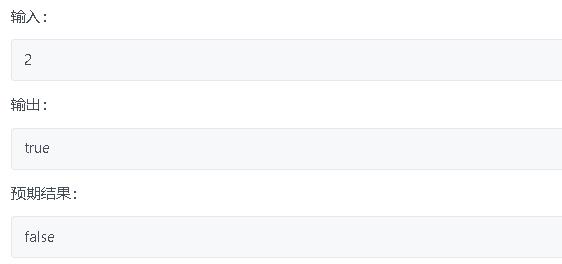
再仔细查看 4^x 的二进制，可以发现其只有奇数位是1，所以，可以定义一个mask值来进行位运算

序号	4x	二进制表示
0	1	0001
1	4	0100
2	16	0001 0000
3	64	0100 0000
4	256	0001 0000 0000

	mask = 0b10101010101010101010101010101010;

或者用一个十六进制数进行表示

	mask = 0xaaaaaaaa;

最终代码

class Solution {
    public boolean isPowerOfFour(int n) {
         return n > 0 && (n & (n - 1)) == 0 && (n & 0xaaaaaaaa) == 0;
    }
}