算法零基础学习关于二维数组的一些基础练习题 | leetcode1672158283248题解

Posted 2021-12-11 过气老学长

目录

• 零 写在前面
• ​1672. 最富有客户的资产总量
• • 问题描述
  • 思路分析
  • 代码
• 1582. 二进制矩阵中的特殊位置
• • 问题描述
  • 思路分析
  • 代码
• 832. 翻转图像
• • 问题描述
  • 思路分析
  • 代码
• 48.旋转图像
• • 问题描述
  • 思路分析
  • 代码

零 写在前面

本篇文章是对 英雄哥 的《算法零基础100讲》（第三讲）中前四道练习题的详细题解。大家可以去 社区 一起学呀！

​1672. 最富有客户的资产总量

问题描述

给你一个 m x n 的整数网格 accounts ，其中 accounts[i][j] 是第 i​​​​​​​​​​​​ 位客户在第 j 家银行托管的资产数量。返回最富有客户所拥有的 资产总量 。

附加信息：

1. 客户的 资产总量 就是他们在各家银行托管的资产数量之和。
2. 最富有客户就是 资产总量 最大的客户。

限制：

1. m == accounts.length
2. n == accounts[i].length
3. 1 <= m, n <= 50
4. 1 <= accounts[i][j] <= 100

思路分析

1. 问题要求返回最富有客户所有的资产总量，根据「附加信息2 」可知，最富有客户=资产总量最大的客户，所以该问题可以拆分为两个小问题：

• 求所有客户的资产总量
• 找出其中的最大值

2. 根据「附加信息1 」可以得知：第 i 位客户的资产总量 = accounts[i] 中元素之和
   这样，思路就明晰了：
   

代码

class Solution {
    public int maximumWealth(int[][] accounts) {
        int sum = 0; // 客户资产计算器
        int max = 0; // 最富有客户的资产值
        for(int i = 0; i < accounts.length; i++){
            // 求每一位客户的总资产
            for(int j = 0; j < accounts[i].length; j++){
                sum += accounts[i][j];
            }
            // 与现有的最富有客户的资产进行比较：如果第i位客户的资产值更大，保存该客户的资产值
            if(max < sum) max = sum;
            // 将「计算器」归零
            sum = 0;
        }
        return max;
    }
}

1582. 二进制矩阵中的特殊位置

问题描述

给你一个大小为 rows x cols 的矩阵 mat，其中 mat[i][j] 是 0 或 1，请返回 矩阵 mat 中特殊位置的数目 。

附加信息
特殊位置：如果 mat[i][j] == 1 并且第 i 行和第 j 列中的所有其他元素均为 0（行和列的下标均 从 0 开始 ），则位置 (i, j) 被称为特殊位置。

限制：

1. rows == mat.length
2. cols == mat[i].length
3. 1 <= rows, cols <= 100
4. mat[i][j] 是 0 或 1

思路分析

这道题最简单的做法就是暴力求解——即对每一个数mat[i][j]检查所在行和所在列是否满足「 特殊位置 」的定义。但是这样的方法过于笨重，而且效率极低（时间复杂度在O(n⁴)）。所以，我们要进行更加深入的思考：
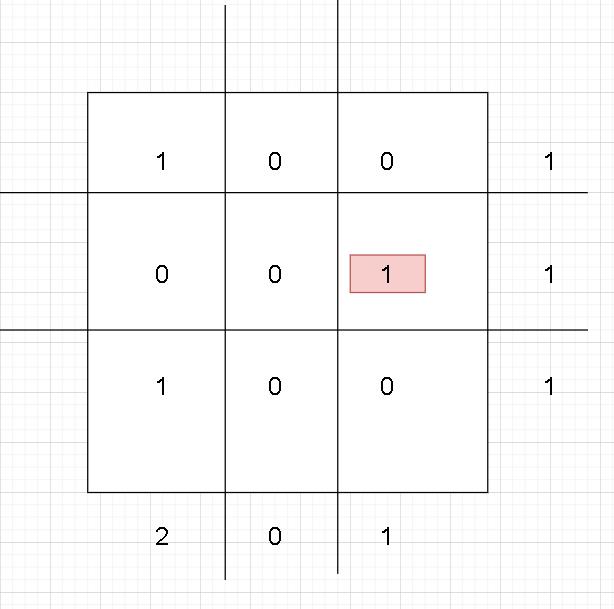我们可以发现，「 特殊位置 」有三个特点：

1. 所在行之和为 1
2. 所在列之和为 1
3. 所处位置上的数字是 1

我们可以利用这个思路进行求解：

代码

class Solution {
    public int numSpecial(int[][] mat) {
        int[] rows = new int[100];
        int[] cols = new int[100];
        int res = 0;
        for(int i = 0; i < mat.length; i++){
            for(int j = 0; j < mat[i].length; j++){
                rows[i] += mat[i][j];
                cols[j] += mat[i][j];
            }
        }
        
        for(int i = 0; i < mat.length; i++){
            
            for(int j = 0; j < mat[i].length; j++){
                if(mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1)
                    res++;
            }
        }

        return res;
    }
}

832. 翻转图像

问题描述

给定一个二进制矩阵 A，我们想先水平翻转图像，然后反转图像并返回结果。

附加信息：

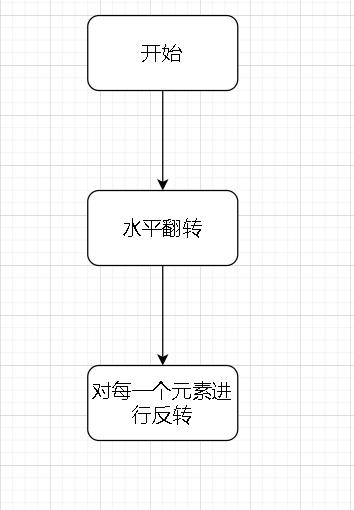
1. 水平翻转图片就是将图片的每一行都进行翻转，即逆序。例如，水平翻转 [1, 1, 0] 的结果是 [0, 1, 1]。
2. 反转图片的意思是图片中的 0 全部被 1 替换， 1 全部被 0 替换。例如，反转 [0, 1, 1] 的结果是 [1, 0, 0]。

限制：

1 <= A.length = A[0].length <= 20
0 <= A[i][j] <= 1

思路分析

代码

class Solution {
    public int[][] flipAndInvertImage(int[][] image) {
        int length = image.length;
        // 先翻转
        for(int i = 0; i < length; i++){
            for(int j = 0; j < length / 2; j++){
                int s = image[i][j];
                image[i][j] = image[i][length - 1 - j];
                image[i][length - 1 - j] = s;
            }
        }
        // 再反转
        for(int i = 0; i < length; i++){
            for(int j = 0; j < length; j++){
                if(image[i][j] == 0){
                    image[i][j] = 1;
                }else{
                    image[i][j] = 0;
                }
            }
        }
        return image;
    }
}

48.旋转图像

这道题可以视为 「832」的一道扩展

问题描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

限制：

matrix.length == n

matrix[i].length == n

1 <= n <= 20

-1000 <= matrix[i][j] <= 1000

思路分析

由于这道题你只能在 原地 进行变换，所以，你需要找到一种方法进行变换。
先观察一个例子：
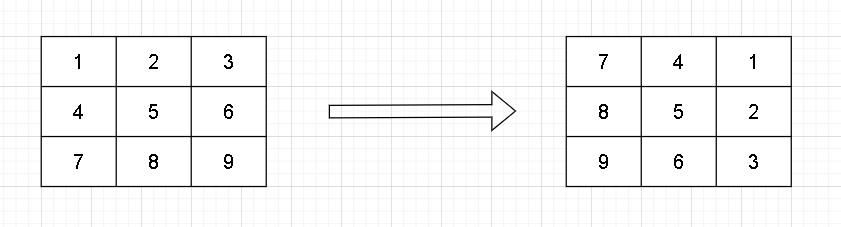我们可以看到：所谓的 「旋转」就是将行变为列，将列变为行。也就是说，将matrix[i][j]元素和 matrix[j][length - 1 - i]元素进行交换。但是遗憾地是，这种方法不可取。

我们再次观察这个例子：

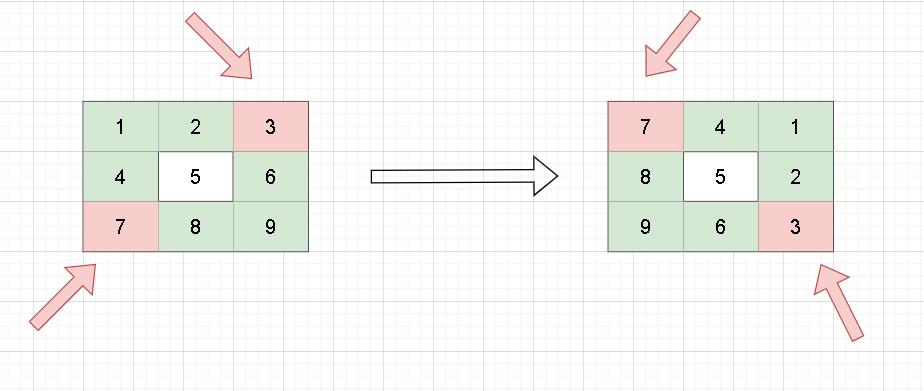
这次，发现下面两个规律：

1. 下面的行变换到了上面
2. 整体沿着对角线翻转

我们可以先对矩阵进行 「上下翻转」，然后再进行「对角线翻转」

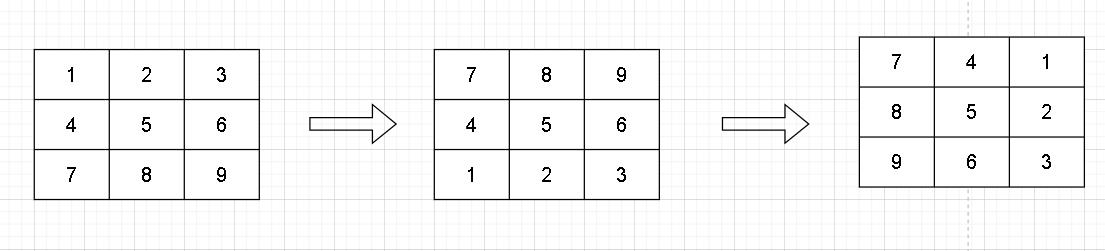
总结一下：

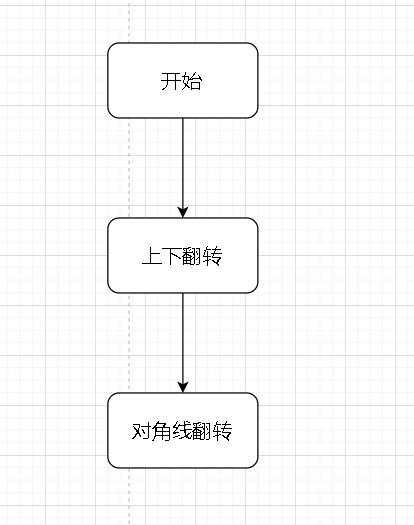
代码

class Solution {
    public void rotate(int[][] matrix) {
        int length = matrix.length;
        //上下翻转
        for(int i = 0; i < length / 2; i++){
            for(int j = 0; j < length; j++){
                int s = matrix[i][j];
                matrix[i][j] = matrix[length - 1 - i][j];
                matrix[length - 1 - i][j] = s;
            }
        }
        //对角线翻转
        for(int i = 0; i < length; i++){
            for(int j = i; j < length; j++){
                int s = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = s;
            }
        }
    }
}