线性代数笔记：Khatri-Rao积

Posted 2021-11-07 UQI-LIUWJ

1 介绍 

   Khatri-Rao积的定义是两个具有相同列数的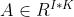矩阵与矩阵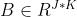的对应列向量的克罗内克积（线性代数笔记：Kronecker积_UQI-LIUWJ的博客-CSDN博客） 排列而成的，其生成的矩阵大小为IJ*K，其表示为：

        

         

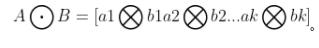
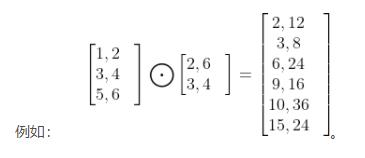
2 性质

 

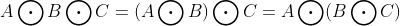
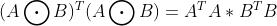
 3 用python实现

import numpy as np
A=np.array([[1,2],[3,4],[5,6]])
B=np.array([[2,6],[3,4]])
np.einsum('ir,jr->ijr',A,B).reshape(-1,A.shape[-1])
'''
array([[ 2, 12],
       [ 3,  8],
       [ 6, 24],
       [ 9, 16],
       [10, 36],
       [15, 24]])
'''

python 笔记：爱因斯坦求和 einsum_UQI-LIUWJ的博客-CSDN博客