虽然小象被淘汰了，但我学会了这种O(n)的排序算法

Posted 2021-11-02 58沈剑

时间复杂度为O(n)的排序，除了昨天介绍的基数排序(Radix Sort)，还有计数排序(Counting Sort)。

计数排序的适用范围？

待排序的元素在某一个范围[MIN, MAX]之间。

画外音：很多业务场景是符合这一场景，例如uint32的数字排序位于[0, 2^32]之间。

计数排序的空间复杂度？

计数排序需要一个辅助空间，空间大小为O(MAX-MIN)，用来存储所有元素出现次数（“计数”）。

画外音：计数排序的核心是，空间换时间。

计数排序的关键步骤？

步骤一：扫描待排序数据arr[N]，使用计数数组counting[MAX-MIN]，对每一个arr[N]中出现的元素进行计数；

步骤二：扫描计数数组counting[]，还原arr[N]，排序结束；

举个栗子：

假设待排序的数组，

arr={5, 3, 7, 1, 8, 2, 9, 4, 7, 2, 6, 6, 2, 6, 6}

很容易发现，待排序的元素在[0, 10]之间，可以用counting[0,10]来存储计数。

第一步：统计计数

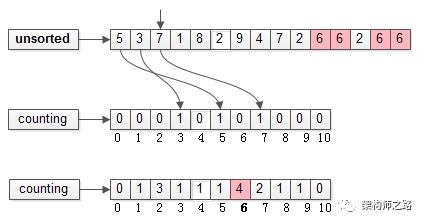
扫描未排序的数组arr[N]，对每一个出现的元素进行计数。

扫描完毕后，计数数组counting[0, 10]会变成上图中的样子，如粉色示意，6这个元素在arr[N]中出现了4次，在counting[0, 10]中，下标为6的位置计数是4。

第二步：还原数组

扫描计数数组counting[0, 10]，通过每个元素的计数，还原arr[N]。

如上图粉色示意，count[0, 10]下标为6的位置计数是4，排完序是4个连续的6。

从counting下标MIN到MAX，逐个还原，填满arr[N]时，排序结束。

神奇不神奇！！！

计数排序(Counting Sort)，总结：

（1）计数排序，时间复杂度为O(n)；

（2）当待排序元素个数很多，但值域范围很窄时，计数排序是很节省空间的；

希望这一分钟，大家有收获。

架构师之路-分享可落地的技术文章

相关文章：

《基数排序，一个O(n)的排序算法

作业题：

还有哪些时间复杂度为O(n)的排序算法呢？