ID3决策树算法|机器学习
Posted 桃陉
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ID3决策树算法|机器学习相关的知识,希望对你有一定的参考价值。
目录
1.ID3决策树原理
1.1基本原理
∙
\\bullet
∙ 基本原理:ID3决策树算法使用信息增益来构建决策树,对于所有的属性我们先选择信息增益最大的作为根节点,然后计算其他属性的信息增益再选择最大的作为子节点,一直递归调用该操作,直到信息增益很小或者没有特征为止。
∙ \\bullet ∙ 根据搭建好的决策树我们带入测试数据的特征就会得到对应的输出结果,那么现在最重要的就是理解什么是信息增益以及如何求解信息增益。
1.2信息熵
∙
\\bullet
∙ 在介绍信息增益之前,先引入信息熵的概念,信息熵是用来衡量样本纯度的指标,我们最终希望的也就是决策树中各分支结点的纯度尽可能的高。信息熵实际上就是信息量的期望,信息量
I
(
x
i
)
I(x_{i})
I(xi) (
x
i
x_{i}
xi 表示样本集合中第
i
i
i 类样本,其实也就是指标签值)的求解如下:
I
(
x
i
)
=
−
𝑙
𝑜
𝑔
2
p
(
x
i
)
\\color{Violet}I(x_{i})=−𝑙𝑜𝑔_{2}p(x_{i})
I(xi)=−log2p(xi)
其中 p ( x i ) p(x_{i}) p(xi) 表示类别为 x i x_{i} xi 类的数据在数据集中出现的概率,由于概率肯定是 [ 0 , 1 ] [0,1] [0,1] 之间的一个数,那么取对数后结果值必然为负数,所以加一个负号来描述。
那么信息量的期望值信息熵的表达式
H
(
X
)
H(X)
H(X) 就为(n为特征值的总数):
H ( X ) = − ∑ i = 1 n p ( x i ) l o g 2 p ( x i ) \\color{Violet}H(X)=-\\sum_{i=1}^{n}p(x_{i})log_{2}p(x_{i}) H(X)=−i=1∑np(xi)log2p(xi)
当求得的 H ( X ) H(X) H(X) 越小时,纯度越高,不确定度越低。我们可以看出当概率等于0或者1时,信息熵为0,此时不确定度最低;而当概率等于0.5时,信息熵等于1,此时不确定度最大。
1.3条件熵
∙
\\bullet
∙ 接下来引入条件熵的概念,由于我们有的时候需要研究某个特征值等于某个具体值的信息熵为多少,这个时候就要用到条件熵。
H
(
Y
∣
X
)
H(Y|X)
H(Y∣X) 表示在特征X的情况下类别Y的熵。计算公式如下:
H
(
Y
∣
X
)
=
∑
i
=
1
n
p
i
H
(
Y
∣
X
=
x
i
)
\\color{Violet}H(Y|X)=\\sum_{i=1}^{n}p_{i}H(Y|X=x_{i})
H(Y∣X)=i=1∑npiH(Y∣X=xi)
其中 H ( Y ∣ X = x i ) H(Y|X=x_{i}) H(Y∣X=xi) 表示在特征 x i x_{i} xi 的分类情况下,不同结果的信息熵; p i p_{i} pi 表示不同结果的数据占该数据集的比例。概率越确定时,条件熵越小。
1.4信息增益
∙
\\bullet
∙ 得到了上面的概念以后我们就可以计算信息增益了,信息增益就是表示我们已知条件
X
X
X 后能得到信息
Y
Y
Y 的不确定性的减少程度。所以就是一个减式,那么特征
A
A
A 对训练集
D
D
D 的信息增益
g
(
D
,
A
)
g(D,A)
g(D,A) 就可以表示为:
g
(
D
,
A
)
=
H
(
D
)
−
H
(
D
,
A
)
\\color{Violet}g(D,A)=H(D)-H(D,A)
g(D,A)=H(D)−H(D,A)
信息增益越大,说明使用该种属性进行划分得到的纯度越大,效果越好。
2.代码实现
2.1计算信息熵calEnt
from math import log
import operator
import numpy as np
#计算信息熵
def calEnt(x,ylabel):
'''
parameters:
x:特征值
ylabel:标签值
returns:
Ent(float):信息熵
'''
numEntries = len(x) #特征值的个数
labelCounts = {} #存放各类标签值数量的字典
#填充字典
for featVec in ylabel:
currentlabel = featVec #记录当前标签
if currentlabel not in labelCounts.keys(): #如果没有出现在字典中则添加
labelCounts[currentlabel] = 0
labelCounts[currentlabel] += 1 #该标签量对应加一
Ent = 0.0 #信息熵
for key in labelCounts:
p = float(labelCounts[key])/numEntries #计算每种类别对应的概率
Ent = Ent - p*log(p,2) #循环求得信息熵
return Ent
2.2获得数据子集splitdataset
#获得数据子集,也就是去掉某一特征值后的子集
def splitdataset(x,ylabel,axis,value):
'''
parameters:
x(ndarray):特征值
ylabel(ndarray):标签值
axis(int):对应的列
value(int):某个具体的值
returns:
subdata(ndarray):截取后的特征值
subylabel(mdarray):截取后的标签值
'''
subylabel = ylabel[x[:,axis]==value] #得到截取后的标签值,x[:,axis]==value表示第得到axis列特征值中等于value的行索引
x = x[x[:,axis]==value,:] #得到截取后的特征值
data1 = x[:,:axis] #选择前axis-1列
data2 = x[:,axis:] #选择axis列后面所有列
subdata = np.hstack([data1,data2]) #相当去去掉axis那一列
return subdata,sublabel
2.3获得最优特征索引
def ID3_chooseBestFeatureToSplit(x,yalbel):
'''
parameters:
x(ndarry):特征值
ylabel(ndarry):标签值
returns:
bestFeature(int):最优特征索引
'''
numFeatures = len(x[0]) #获得特征值的特征列数
baseEnt = calEnt(x,ylabel) #计算基础信息熵
bestInfoGain = 0.0 #定义最优信息增益
bestFeature = -1 #定义最优特征值的索引
#遍历计算所有特征值的特征增益
for i in range(numFeatures):
featList = [example[i] for example in x] #取出该列的所有特征值
uniqueVals = set(featList) #去重,便于下面遍历计算
nweEnt = 0.0 #定义条件熵
for value in uniqueVals: #分别计算每种划分方式下的条件熵
subdataset,subylabel = splitdataset(x,ylabel,i,value)
p = len(subdataset)/float(len(x))
newEnt +=p*calEnt(subdataset,subylabel)
infoGain = baseEnt - newEnt #计算该属性的信息增益
print(u"ID3中第%i特征的信息增益为:%.3f"%(i,infoGain))
if(infoGain>baseInfoGain): #若找到更优信息增益则更新
bestInfoGain = infoGain
bestFeature = i
return bestFeature
2.4处理样本中只有一个特征或者特征都一样的情况
#数据集已经处理了所有属性,但是类标签依然不是唯一的
#此时我们需要决定如何定义该叶子节点,在这种情况下,我们通常会采用多数表决的方法决定该叶子节点的分类
def majorityCnt(classList):
'''
parameters:
classList(list):标签值列表
returns:
bestFeature(int):最优特征值
'''
classCont={}#创建空字典
#给所有可能分类创建字典
for vote in classList:
#如果vote之前没有在字典里出现过,则新建key值,并赋值为0
if vote not in classCont.keys():
classCont[vote]=0
classCont[vote]+=1#vote每多出现一次,字典值加1
sortedClassCont=sorted(classCont.items(),key=operator.itemgetter(1),reverse=True)#将字典classCont按照字典值由大到小排列
bestFeature=sortedClassCont[0][0]#得到字典第一个值的key值,即最优特征
return bestFeature
2.5创建ID3决策树
def ID3_createTree(x,ylabel,xlabel):
'''
parameters:
x(ndarry):特征值
ylabel(ndarry):标签值
xlabel(list):特征值标签列表
returns:
bestFeature(int):最优特征索引
'''
classList = list(ylabel)
if classList.count(classList[0])==len(classList):
return classList[0]
if len(x[0])==1:
return majorityCnt(classList)
bestFeat = ID3_chooseBestFeatureToSplit(x,ylabel)
bestFeatLabel = xlabel[bestFeat]
print(u"此时最优索引为:"+str(bestFeatLabel))
ID3Tree = {bestFeatLabel:{}}
xlabel.pop(bestFeat)
featValues = [example[bestFeat] for example in x]
uniqueVals = set(featValues)#将特征列表创建成为set集合,元素不可重复。创建唯一的分类标签列表
for value in uniqueVals:#根据每种划分方式继续构造ID3决策树分支
subxlabel = xlabel[:]#得到子集的特征值标签
subdataset,subylabel=splitdataset(x,ylabel, bestFeat, value)#得到子集的特征值和标签值
ID3Tree[bestFeatLabel][value] = ID3_createTree(subdataset,subylabel,subxlabel)#递归,继续构造ID3决策树分支
return ID3Tree
2.6返回一条测试数据的标签值以及返回测试集数据的标签列表
#返回一条测试数据的标签值
def classify(inputTree, xlabel, testVec):
'''
parameters:
inputTree:训练好的决策树
xlabel(list):特征值标签列表
testVec(ndarray):一条测试数据
returns:
classLabel(str):特征值标签
'''
firstStr = list(inputTree.keys())[0]#得到字典的第一个key值
secondDict = inputTree[firstStr]#根据key值得到下一个字典
featIndex = xlabel.index(firstStr)#根据key值得到索引
classLabel = '0'#定义变量classLabel,默认值为0
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':#判断secondDict[key]是否是字典格式
classLabel = classify(secondDict[key], xlabel, testVec)#如果是字典格式,进行递归
else:
classLabel = secondDict[key]#如果不是字典格式,得到特征标签
return int(classLabel)
#返回测试数据集的标签值列表
def classifytest(inputTree, xlabel, testDataSet):
'''
parameters:
inputTree:训练好的决策树
xlabel(list):特征值标签列表
testDataSet(ndarray):测试数据集
returns:
classLabelAll(list):特征值标签列表
'''
classLabelAll = []#创建空列表
for testVec in testDataSet:#遍历每条数据
classLabelAll.append(classify(inputTree, xlabel, testVec))#将每条数据得到的特征标签添加到列表
return np.array(classLabelAll)
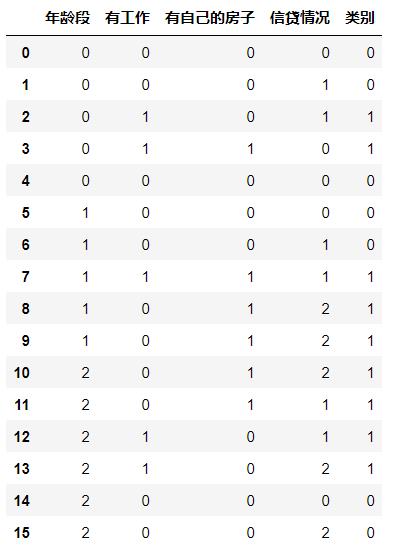
3.实例
∙
\\bullet
∙ 年龄段:0代表青年,1代表中年,2代表老年;
∙
\\bullet
∙ 有工作:0代表否,1代表是;
∙
\\bullet
∙ 有自己的房子:0代表否,1代表是;
∙
\\bullet
∙ 信贷情况:0代表一般,1代表好,2代表非常好;
∙
\\bullet
∙以上是关于ID3决策树算法|机器学习的主要内容,如果未能解决你的问题,请参考以下文章