[Atcoder ABC222] F - Expensive Expense | 妙用树的直径 | Dijkstra

Posted 2021-10-29 PushyTao

Time Limit: 4 sec / Memory Limit: 1024 MB
Score : 500 points

Problem Statement

The Kingdom of AtCoder is composed of $N$ towns and $N-1$ roads.
The towns are labeled as Town 1, Town 2, …, Town N. Similarly, the roads are labeled as Road 1, Road 2, …, Road N−1. Road i connects Towns $A_i$ and $B_i$ bidirectionally, and you have to pay the toll of $C_i$ to go through it. For every pair of different towns $(i,j)$, it is possible to go from Town $A_i$ to Town $B_j$ via the roads.
You are given a sequence $D=(D_1,D_2,\dots ,D_N)$, where $D_i$ is the cost to do sightseeing in Town i. Let us define the travel cost $E_{i,j}$ from Town $i$ to Town $j$ as the total toll incurred when going from Town $i$ to Town $j$, plus $D_j$. More formally, $E_{i,j}$ is defined as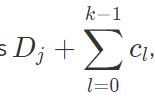
, where the shortest path between $i$ and $j$ is $i=p_0,p_1,\dots ,p_{k-1},p_k=j$ and the toll for the road connecting Towns $p_l$ and $p_{l+1}$ is $c_l$.
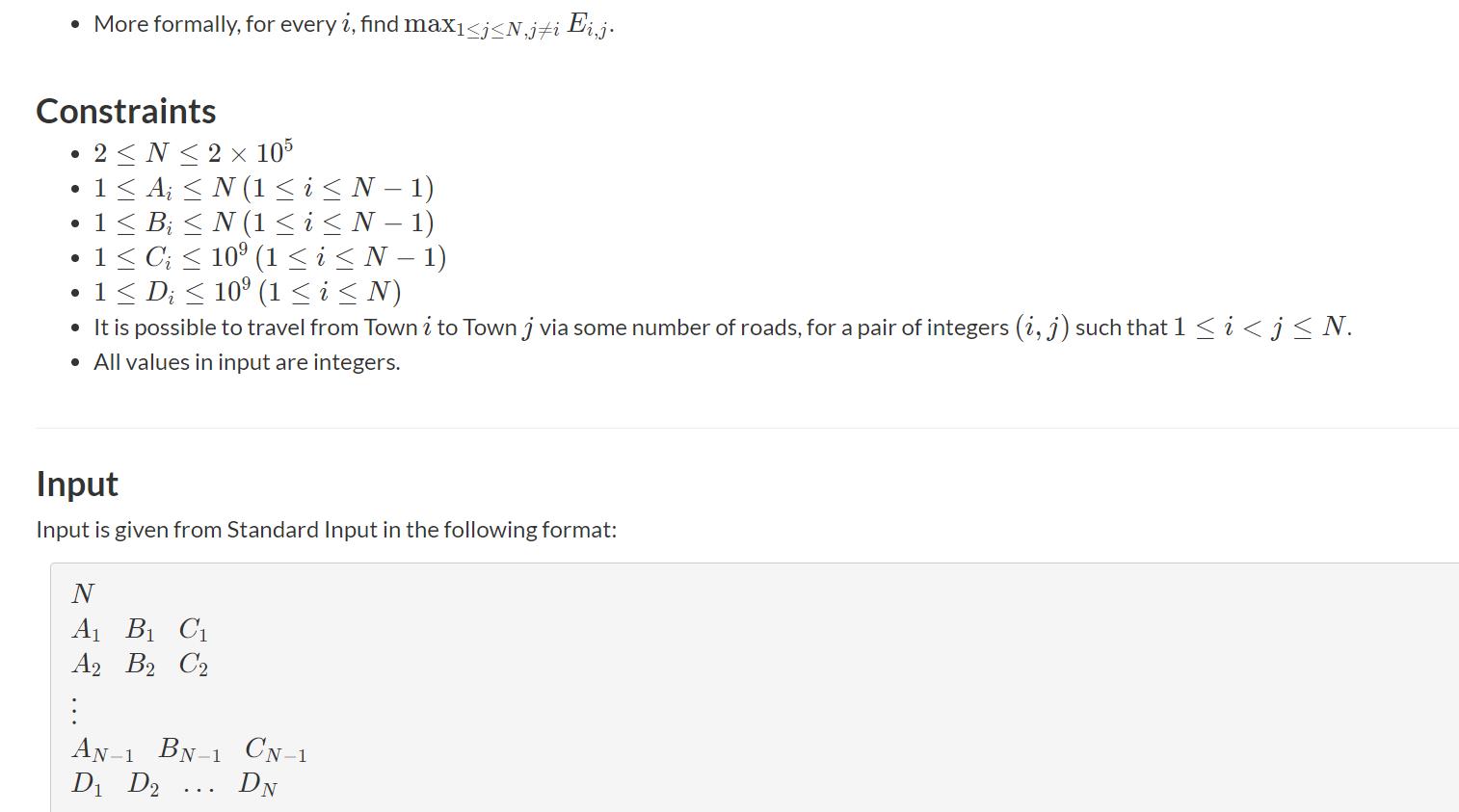
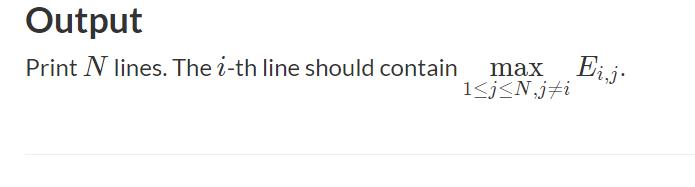
For every i, find the maximum possible travel cost when traveling from Town i to another town.

Sample Input 1
Copy

3
1 2 2
2 3 3
1 2 3

Sample Output 1
Copy

8
6
6

Sample Input 2
Copy

6
1 2 3
1 3 1
1 4 4
1 5 1
1 6 5
9 2 6 5 3 100

Sample Output 2
Copy

105
108
106
109
106
14

Sample Input 3
Copy

6
1 2 1000000000
2 3 1000000000
3 4 1000000000
4 5 1000000000
5 6 1000000000
1 2 3 4 5 6

Sample Output 3
Copy

5000000006
4000000006
3000000006
3000000001
4000000001
5000000001

不得不说题解给的很妙

1. 树的直径
2. 换根dp
   树的直径：
   树中任意两点之间的最短距离的最大值，即为树的直径，树的直径是树上两点之间的距离的最大值，对于题目中给定的代表节点游览花费$D$数组，对于某一个节点$u$的值$D[u]$我们可以当最是有另外的一个节点$u^{\prime }$与u连了一条值为$D[u]$，然后在找直径的时候顺便把$D$考虑进去，然后找到树的直径的两个端点之后，在进行两次最短路，分别将得到的距离$dis[]$存放起来
   下面在算贡献的时候，直接找该点到端点（记得是两个）的距离的最大值即可

方法1：

#define Clear(x, val) memset(x, val, sizeof x)
typedef pair<ll, int> PII;
int cnt, head[maxn];
struct node {
    int u, v, nex;
    ll w;
} e[maxn << 1];
void init() {
    Clear(head, -1);
    cnt = 0;
}
void add(int u, int v, ll w) {
    e[cnt].u   = u;
    e[cnt].v   = v;
    e[cnt].w   = w;
    e[cnt].nex = head[u];
    head[u]    = cnt++;
}
ll dis[maxn];
bool vis[maxn];
void Dijkstra(int x) {
    memset(dis, 0x3f3f3f3f, sizeof dis);
    Clear(vis, 0);
    dis[x] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> que;
    que.push({dis[x], x});
    while (que.size()) {
        PII top = que.top();
        que.pop();
        ll w    = top.first;
        int u   = top.second;
        if (vis[u]) continue;
        vis[u] = 1;
        for (int i = head[u]; ~i; i = e[i].nex) {
            int to = e[i].v;
            if (dis[to] > w + e[i].w) {
                dis[to] = dis[u] + e[i].w;
                if (!vis[to]) {
                    que.push({dis[to], to});
                }
            }
        }
    }
}
ll cost[maxn];
ll dis2[maxn];
int n;
int main() {
    n = read;
    init();
    for (int i = 1; i < n; i++) {
        int u = read, v = read;
        ll w = read;
        add(u, v, w);
        add(v, u, w);
    }
    for (int i = 1; i <= n; i++) cost[i] = read;
    Dijkstra(1);
    ll mx   = -1;
    int pos = 0;
    for (int i = 1; i <= n; i++) {
        if (i == 1) continue;
        if (cost[i] + dis[i] > mx) {
            mx  = cost[i] + dis[i];
            pos = i;
        }
    }
    Dijkstra(pos);
    int pos2 = 0;
    mx       = -1;
    for (int i = 1; i <= n; i++) {
        if (i == pos) continue;
        if (cost[i] + dis[i] > mx) {
            mx   = cost[i] + dis[i];
            pos2 = i;
        }
    }
    /// the long_est one is from pos to pos2
    Dijkstra(pos);
    for (int i = 1; i <= n; i++) dis2[i] = dis[i];
    Dijkstra(pos2);
    for (int i = 1; i <= n; i++) {
        ll out = 0;
        if (i != pos) out = max(out, dis2[i] + cost[pos]);
        if (i != pos2) out = max(out, dis[i] + cost[pos2]);
        cout << out << endl;
    }
    return 0;
}