经典卷积概述

Posted 2021-10-27 骨灰小鱼人提莫

        本文内容主要是对一些经典卷积的概述，包括现代CNN的基本构建模块，可变形卷积，组卷积，可控制卷积，等等。

CNN

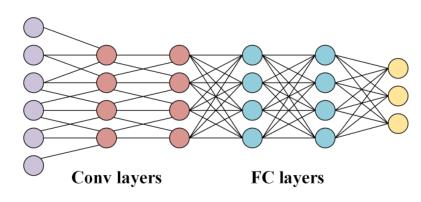
图1.CNN层和FC层示意图

        首先介绍一下卷积神经网络(CNN)，CNN有以下三个特点：

1. 局部连接——每个神经元不再与前一层的所有神经元相连，而只与少数神经元相连，有效地减少了参数，加快了收敛速度。
2. 权值共享——一组连接可以共享相同的权值，这进一步减少了参数。
3. 降采样降维—池化层利用图像局部相关原理对图像进行降采样，在保留有用信息的同时减少数据量。它还可以通过去除琐碎的特征来减少参数的数量。

       

 

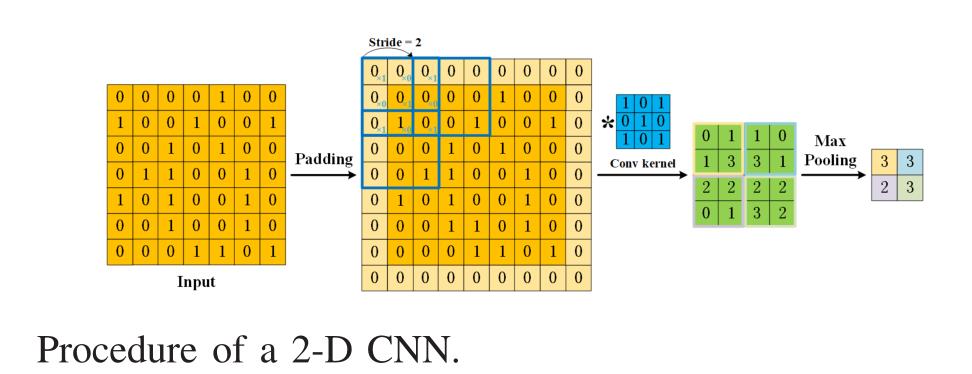
        构建CNN模型，通常需要四个组件：1）卷积是特征提取的关键步骤，卷积的输出可以是特征图2）当设置一个一定大小的卷积核时，我们会丢失边界上的信息。因此，采用填充零值的方法，间接调节输入的大小。3）为了控制卷积的密度，设置步幅Stride = .步幅越大，密度越低。4）卷积后的特征图由大量容易引起过拟合问题的特征组成。为了消除冗余，提出了池化方法，包括最大池化和平均池化。

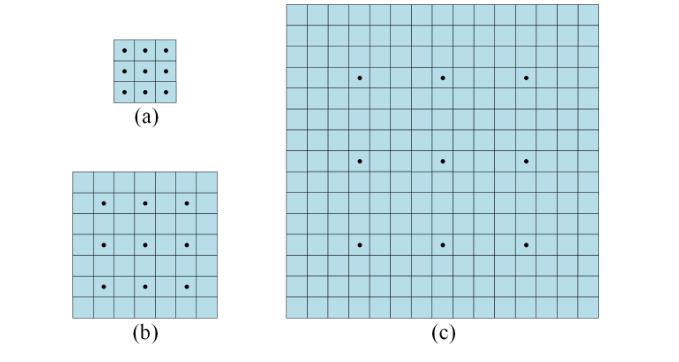
        为了使卷积核能够感知更大的区域，提出了扩张卷积。注意，每个卷积核点之间都有一个空值(用0填充)。即使有效的核点仍然是3×3，双扩张卷积有7×7的接受域，四扩张卷积有15×15的接受域。

Deformable Convolution

        针对物体形状不规则的情况，提出了可变形卷积算法。该算法关注它们感兴趣的内容，使特征图具有代表性。利用并行卷积层学习偏移量，并将其添加到卷积核的原始位置，实现尺度变换，这些偏移量适应了目标对象的尺度变换，增加了卷积核的接受域。第二种是可变形感兴趣区域池模块。可变形池模块使用一个完整的连接层来学习特征的偏移量，然后执行池化。研究发现，尽管可变形卷积可以适应几何变换，并通过移动卷积核单元来扩展接受域，但训练受到许多与可用域无关的特征的影响。    

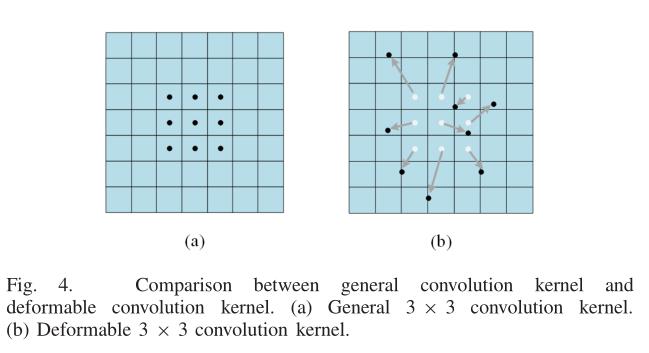
 Group Convolution

           

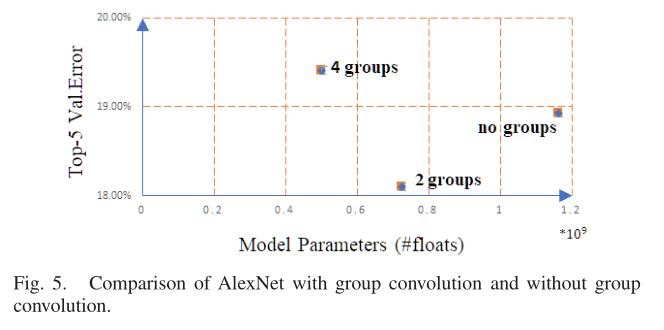
         首次将组卷积应用于AlexNet，以低GPU资源消耗的方式训练深层CNN。用群卷积代替普通卷积可以构建更宽的网络并减少参数。此外，群卷积可以更好地学习表示并保证精度。如图5所示，与其他两组相比，没有组卷积的AlexNet效率更低，精确度更低。

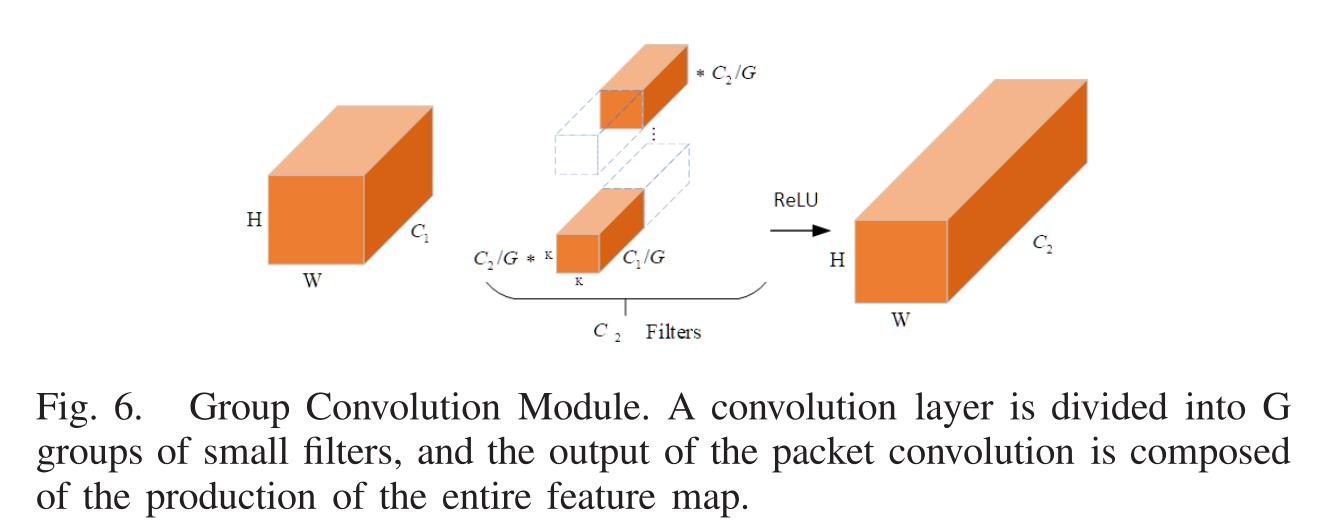
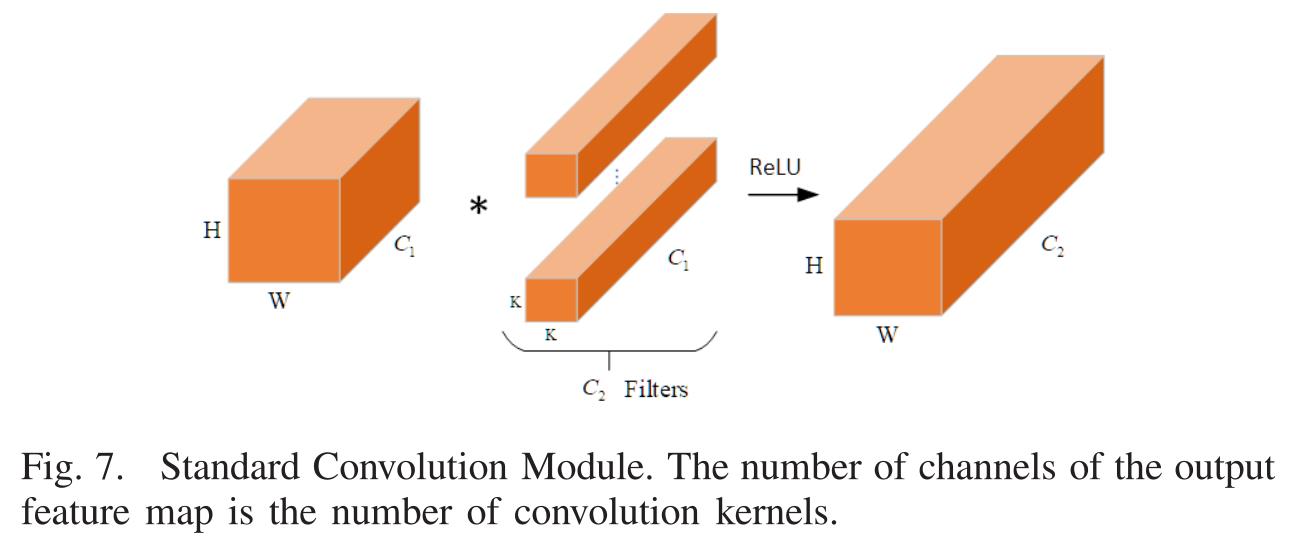
        群卷积滤波器组在信道维数上学习稀疏对角块结构的特征。与图7中的标准卷积相比，通过减少参数的数量，不太可能导致过拟合。为了减少设计负担，ResNeXt中使用的较小的卷积块具有相同的拓扑结构。ResNeXt的实验结果也证明，增加堆叠块的数量比仅仅增加网络的宽度和深度更有效。

        第一步是压缩阶段。经过稀疏诱导正则化训练后，对权重较低的非必要滤波器进行修剪。第二步是优化阶段。在每个组的权值固定后，继续进行训练，确保同一组卷积具有相同的稀疏模式。

        但是这种人工选择群卷积的方法仍然缺乏优势。因此，zhangable ConvNet等人提出了一种将网络架构搜索(network architecture search, NAS)与群卷积相结合的Groupable ConvNet，它可以使用端到端方法自动学习组的数量。

 Steerable Convolution

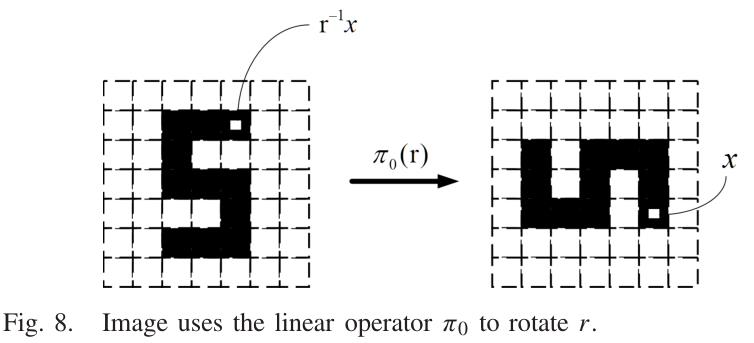
        在许多视觉任务中，增强网络的等变性是至关重要的。我们通常希望网络是等变的，而不是不变的。如图8所示，对属于线性空间的图像进行旋转后，不变网络不再能够进行准确的识别。更具体地说，例如在一幅抽象画中，一张面部特征异常的脸，仍然可以在不变卷积网络中被识别为具有正常特征的脸。因此，我们想要CNN具有等变形，以在输入发生变换时仍然可以产生一个可预测的线性表示。筛选器不仅能适应像标准CNN一样的位置变化，还能适应姿势变化。

        如图9所示，他们在一组中引入了各种形式的线性变换。它有助于提高等变CNN的灵活性，以及解耦群的规模和计算复杂度。此外，可操作CNN可以很容易地扩展到连续设置，评估可操作CNN对于大型和高维群体是未来工作的重要组成部分。 

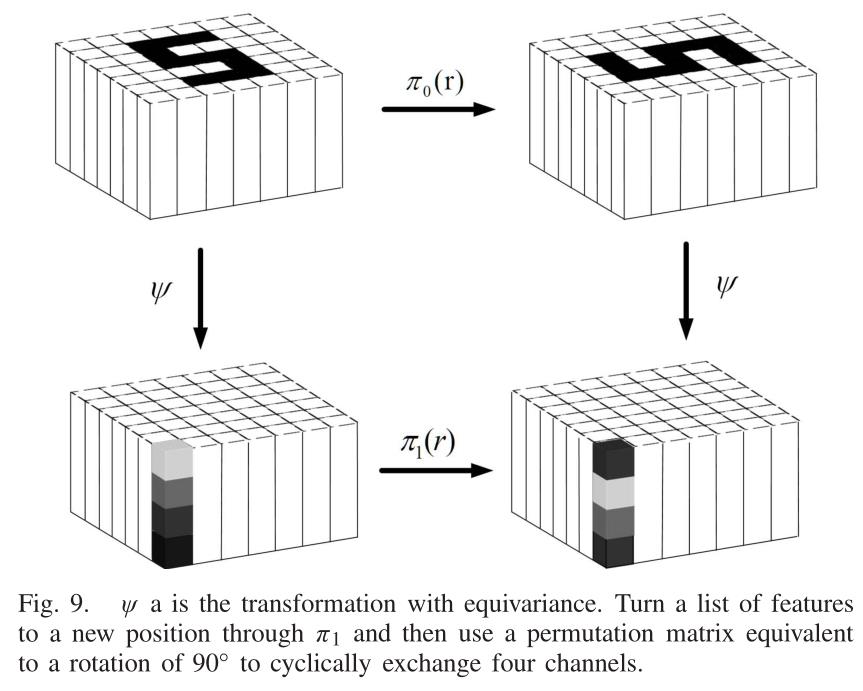
        Weiler et al.在可操纵CNN的基础上，提出了等价于刚体运动的三维可操纵CNN，利用标量场、矢量场和张量场表示三维欧氏空间中的数据，并利用等变卷积映射这些表示。此外，给出了作为核空间通解的欧几里德群E(2)[及其子群，以适应平面像的旋转和反射。 

Graph Convolution

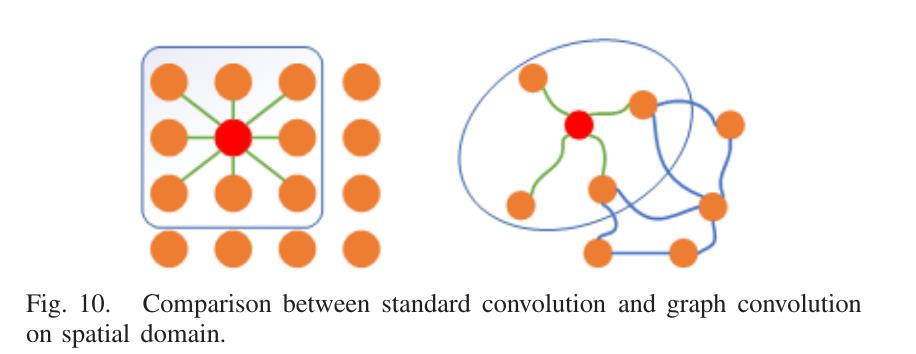
        图神经网络(GNN)是近年来研究的热点之一。利用Goriet等人提出的最早的基于不动点理论的GNN解决了这一问题。他们在预处理阶段将图转换为一维矩阵，导致拓扑信息丢失。Scarselliet al.将现有的神经网络方法扩展到处理图域数据。他们提出了一个GNN模型，可以直接处理更多类型的图，如循环图、有向图和无向图。由于卷积神经网络不能在非欧几里德空间学习数据，所以之前的GNN模型不能与卷积结合。这成为GNN需要突破的瓶颈。Brunaet al.发现CNN可以在其域内使用信号类的局部平移不变性，这在图像和音频识别任务中非常有用。他们提出了两种GNN结构。一种基于域的层次聚类，另一种基于图拉普拉斯谱。Kipf和Welling提出了一种图卷积网络(GCN)。他们通过频谱图卷积的局部一阶近似来激发卷积结构的选择。GCN模型线性扩展图的边数，学习编码局部图结构和节点特征的隐含层表示。图的卷积方法可以分为两种:空间域卷积和频域卷积与图10中空间域的卷积相比，频率域的卷积对于图信号的处理具有实际的理论基础。GCN是一种基于频域卷积的方法，滤波一个卷积网络，通过傅里叶变换将处理后的信号映射到频域。从空间域的角度考虑，GCN从节点的邻域聚合特征信息，并通过寻找备选对称矩阵逐步改进。Liet al.提出的自适应GCN，使用具有两节点特征的可学习距离函数作为输入构造残差图。残差图的邻接矩阵可以学习到未指定的隐藏结构关系。Zhuang和Ma通过并行化两个图卷积层实现了一个双gcn (DGCN)。通过集成双图卷积层的输出，DGCN可以捕获局部和全局结构信息，而不需要利用多个图卷积层。传统的CNN对图像上的像素进行卷积，而基于空间域的图卷积通过图中节点的空间关系定义卷积。如图10所示，它将中心节点的表示与相邻节点的表示进行卷积，并获得中心节点的更新表示。空间域卷积的节点信息基本上沿边缘传播。Micheli提出了第一个基于空间域的图卷积神经网络，称为图的神经网络（NN4G）。它通过直接累积邻居节点的信息来执行卷积。为了记录每一层的特征，NN4G使用剩余结构和跳过连接。 

        经典CNN模型的一部分。NiN：网络中的网络；ResNet：剩余netwrok；深卷积生成对抗网络；SENet：挤压和激励网络。