toch_geometric 笔记：message passing

Posted 2021-10-25 UQI-LIUWJ

1 message passing介绍

        将卷积算子推广到不规则域通常表示为一个邻域聚合（neighborhood aggregation）或消息传递（message passing ）方案

        给定第(k-1)层点的特征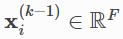，以及可能有的点与点之间边的特征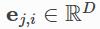，依靠信息传递的GNN可以被描述成：

 

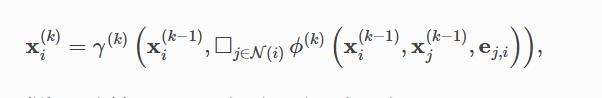
 其中表示一个可微分的可微，置换不变的函数（比如sum、mean或者max），γ和Φ表示可微分方程（比如MLP）

 

2 message passing 类  

        PyG提供了message passing基类，它通过自动处理消息传播来帮助创建这类消息传递图神经网络。

        使用者只需要定义γ（update函数）和Φ（message函数），以及聚合方式aggr（即）【aggr="add", aggr="mean" or aggr="max"】即可

2.1 MessagePassing

MessagePassing(
    aggr="add", 
    flow="source_to_target", 
    node_dim=-2)

 定义了聚合方式（这里是’add‘）

信息传递的流方向（"source_to_target" 【默认】or "target_to_source"）

node_dim表示了沿着哪个轴进行传递

2.2 MessagePassing.propagate

MessagePassing.propagate(
    edge_index, 
    size=None, 
    **kwargs)

        开始传播消息的初始调用。

        获取边索引（edge index）和所有额外的数据，这些数据是构造消息和更新节点嵌入所需要的。

        propagate()不仅可以在[N,N]的邻接方阵中传递消息，还可以在非方阵中传递消息，（比如二部图[N,M]，此时设置size=(N,M)作为额外的形参）

        如果size参数设置为None，那么矩阵默认是一个方阵。

        对于二部图[N,M]来说，它有两组互相独立的点集，我们还需要设置x=(x_N,x_M)

2.3 MessagePassing.message(...)

        类似于Φ。将信息传递到节点i上。 如果flow="source_to_target"，那么是找所有(j,i)∈E；如果flow="target_to_source"，那么找所有(i,j)属于E。

        可以接受最初传递给propagate()的任何参数。

        此外，传递给propagate()的张量可以通过在变量名后面附加_i或_j，映射到各自的节点。例如，x_i（表示中心节点）、 x_j（表示邻居节点）。

        注意，我们通常将i称为汇聚信息的中心节点，将j称为相邻节点，因为这是最常见的表示法。

2.4 MessagePassing.update(aggr_out, ...)

        类比γ，对每个点i∈ V，更新它的node embedding

        第一个参数是聚合输出，同时将所有传递给propagate()的参数作为后续参数

3 举例： GCN

3.1 GCN回顾

GCN层可以表示为：

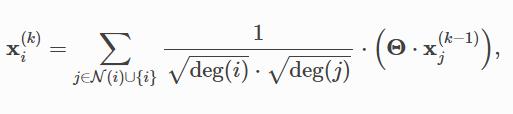
         k-1层的邻居节点先通过权重矩阵Θ加权，然后用中心节点和这个邻居节点的度来进行归一化，最后求和聚合 。

3.2 message passing 实现过程

        这个方程可以划分成以下几个步骤

1. 在邻接矩阵中添加自环（因为上式Σ的下标中，除了i的邻居，还有i本身）
2. 线性变换特征矩阵
3. 计算归一化系数
4. 归一化邻居/上一层的自己的点特征 （Φ，即message操作） 
5. 求和邻居节点、自身的点特征（“add”，γ操作）

        步骤1~3在message passing开始前就已经计算完毕了；步骤4，5则可以用MessagePassing操作来进行处理 。

3.3 代码解析

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super().__init__(aggr='add') 
        # "Add" aggregation (Step 5).
        #GCN类从MessagePssing中继承得到的聚合方式：“add”
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        # x has shape [N, in_channels] ——N个点，每个点in_channels维属性
        # edge_index has shape [2, E]——E条边，每条边有出边和入边

        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
        #添加自环

        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)
        #对X进行线性变化

        # Step 3: Compute normalization.
        row, col = edge_index
        #出边和入边
        deg = degree(col, x.size(0), dtype=x.dtype)
        #各个点的入度（无向图，所以入读和出度相同）
        deg_inv_sqrt = deg.pow(-0.5)
        deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
        #1/sqrt(di) *1/sqrt(dj)

        # Step 4-5: Start propagating messages.
        return self.propagate(edge_index, x=x, norm=norm)
        #进行propagate
        #propagate的内部会调用message(),aggregate()和update()
        #作为消息传播的附加参数，我们传递节点嵌入x和标准化系数norm。    

    def message(self, x_j, norm):
        # x_j has shape [E, out_channels]
        #我们需要对相邻节点特征x_j进行norm标准化
        #这里x_j为一个张量，其中包含每条边的源节点特征，即每个节点的邻居。

        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_j
        #1/sqrt(di) *1/sqrt(dj) *X_j

  之后，我们就可以用这种方法轻松调用了：

conv = GCNConv(16, 32)
x = conv(x, edge_index)