神经网络——BP学习算法推导
Posted 土味儿大谢
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了神经网络——BP学习算法推导相关的知识，希望对你有一定的参考价值。
参考书籍：人工智能及其应用（第三版） 王万良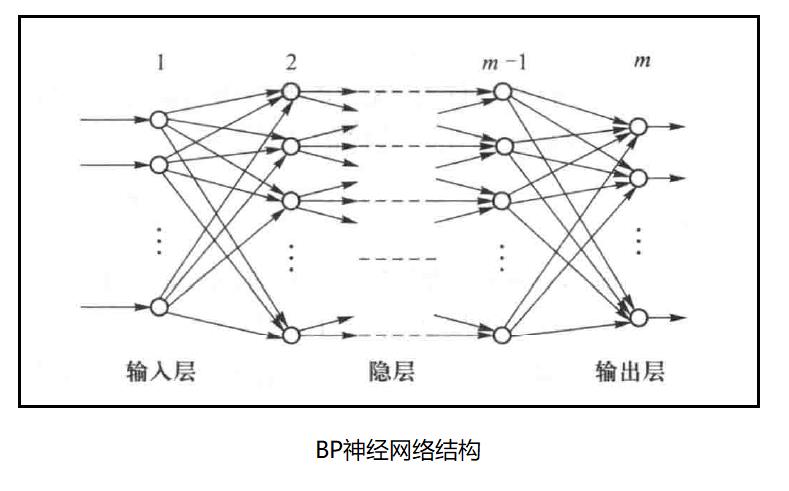
输入层的神经元的输入输出关系一般是线性函数
隐层(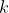
)中神经元的输入输出关系一般是非线性函数
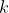与输出层中各个神经元的非线性输入输出关系记为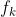
第
层的第
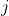个神经元到第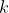层的第
个神经元的连接权值为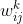
。
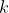层中第个神经元输入的总和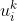为
，输出为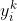
综上各变量之间的关系为 式1
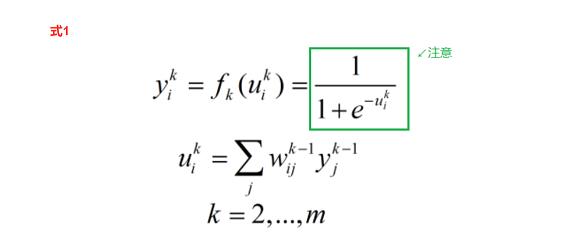
BP学习算法是通过反向学习过程使误差最小，其目标函数为 式2
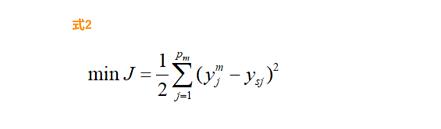
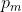：输出层神经元个数
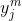：实际输出
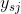：期望输出
取平方项是为了避免值抵消，乘1/2是因为要求导抵消²
式2 即是求期望输出与实际输出之差的平方和最小。就是求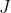
的极小值。约束条件就是 式1。因为要求极小值，所以需要对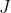求导，即神经网络权值的修正量为 式3
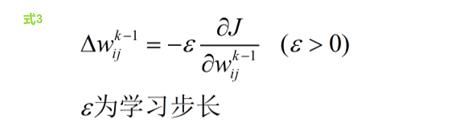
为什么要对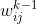
求导呢？因为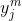-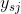=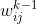。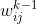由式1可以知道是第
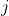层的第个神经元到第层的第个神经元的连接权值。要使连接权值最小所以对他求导。乘以-
是因为目标函数是沿着负梯度方向改变的。
下面是推导BP学习算法的完整过程：
先求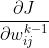 
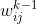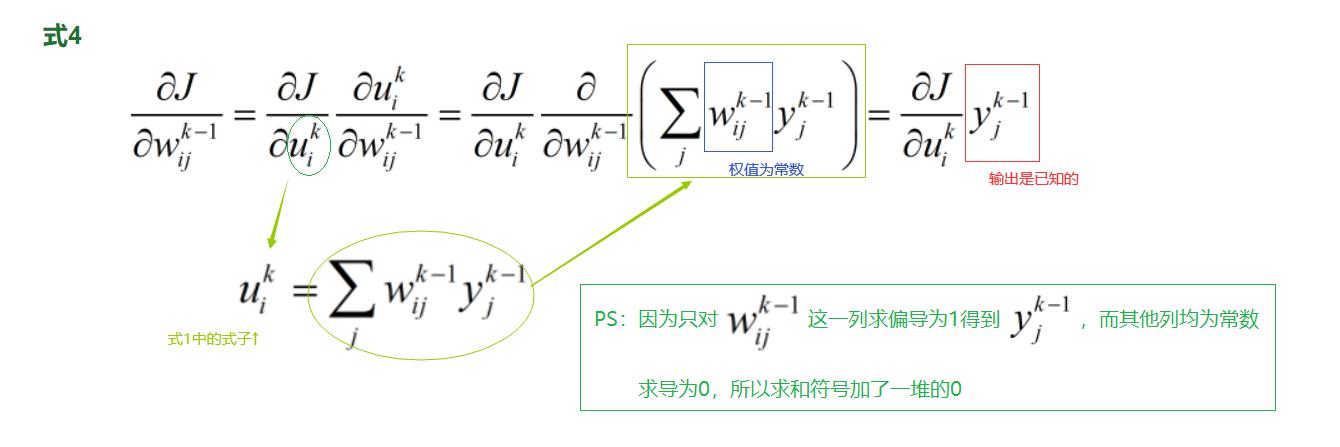
因为在 式1 中的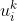里面，所以采用链式求导得到 式4
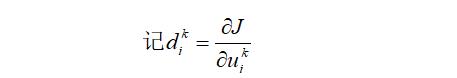
则 式3 变为 式5
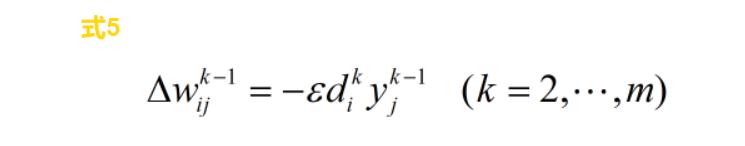
接下来开始推导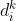 
得到 式6
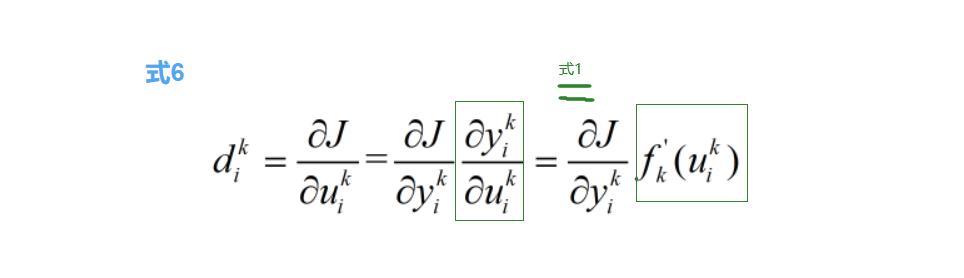
下面分两种情况求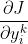 
①对输出层（第m层）的神经元，即 
，
，有误差定义式得
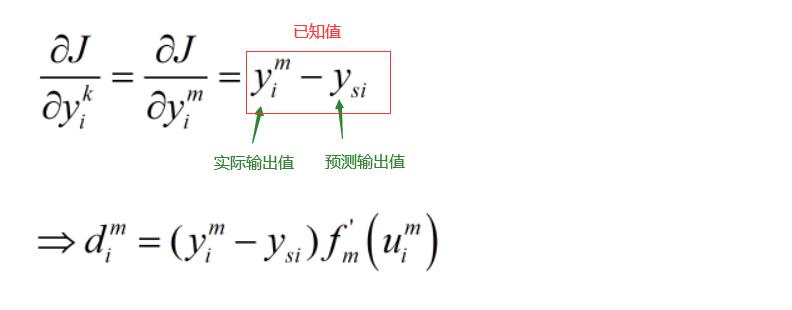
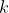②若 为隐单元层 ，则有
综上所述，BP学习算法可以归纳为
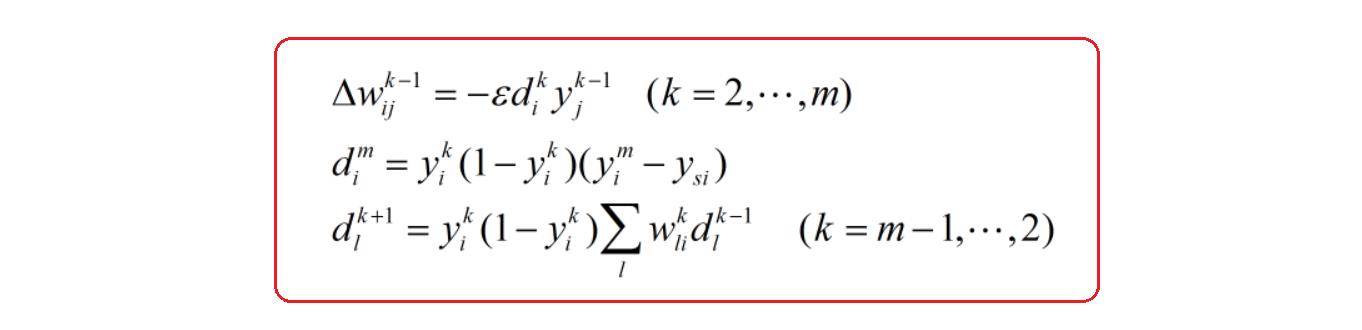
若取 
为 
型函数，即（式1有给出）
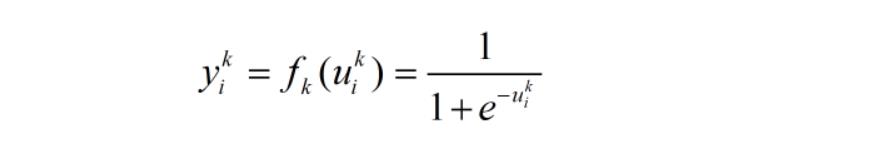
则
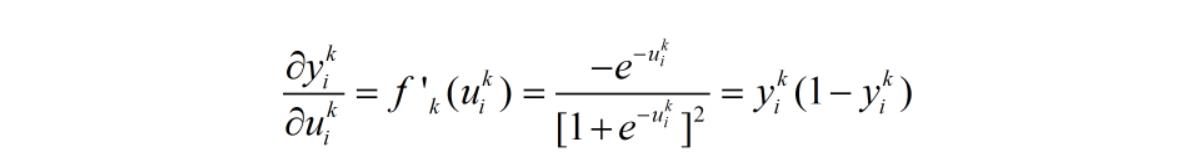
BP学习算法可以归纳为
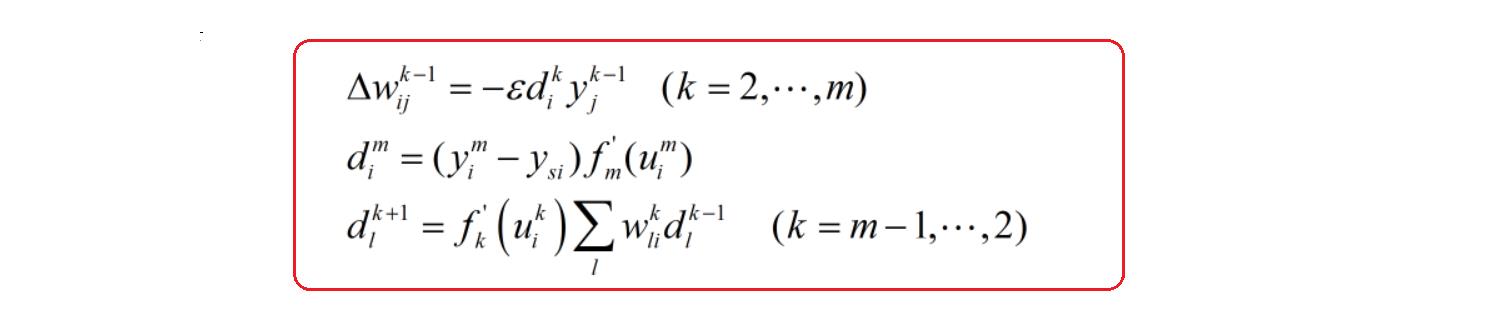
以上是关于神经网络——BP学习算法推导的主要内容，如果未能解决你的问题，请参考以下文章