2019牛客多校Monotonic Matrix
Posted Jozky86
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2019牛客多校Monotonic Matrix相关的知识,希望对你有一定的参考价值。
题意:
问有多少个n * m的矩阵A满足一下情况:答案mod 1e9+7
- 矩阵A的所有元素∈{0,1,2}
- A i , j < = A i + 1 , j A_{i,j}<=A_{i+1,j} Ai,j<=Ai+1,j
- A i , j < = A i , j + 1 A_{i,j}<=A_{i,j+1} Ai,j<=Ai,j+1
题解:
我们先看看这个式子有啥规律?
对于每一行,每一列都是非下降序列,也就是说如果有一位是2,其后面都是2,如果有一位是1,其前面都是1
那我们考虑元素01和12的分界线
是(n,0)到(0,m)的两条不相交(可重合的路径)
第一个分界线以上的点是一种,两条分界线之间是一种,第二个分界线以下是一种(详细看图)
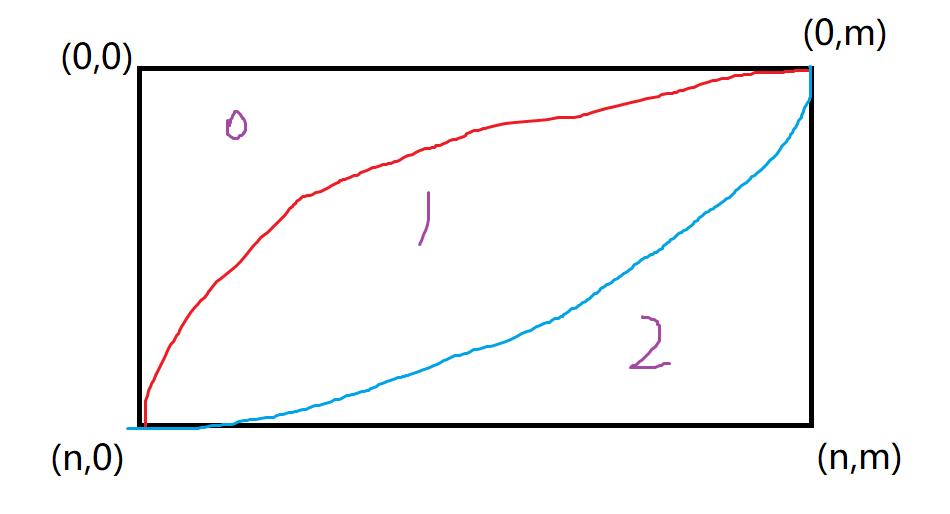
不过现在这个两个线的起终点一样,我们可以将第一个线进行偏移,变成起点为(n-1,-1)到(-1,m-1).(注意这两个线不是弧形的,而是水平竖直线)
现在问题就是起点为(n-1,-1),终点为(-1,m-1)和起点为(n,0),终点为(0,m),两个不相交路径的条数
怎么做?引入LGV定理
就有:
起点{
a
1
,
a
2
a_{1},a_{2}
a1,a2}={
(
n
,
0
)
,
(
n
−
1
,
−
1
)
(n,0),(n-1,-1)
(n,0),(n−1,−1)}
终点{
b
1
,
b
2
b_{1},b_{2}
b1,b2}={
(
0
,
m
)
,
(
−
1
,
m
−
1
)
(0,m),(-1,m-1)
(0,m),(−1,m−1)}
带入公式:
a
n
s
=
∣
(
a
1
,
b
1
)
(
a
1
,
b
2
)
(
a
2
,
b
1
)
(
a
2
,
b
2
)
∣
ans= \\begin{vmatrix} (a_{1},b_{1})&(a_{1},b_{2})\\\\ (a_{2},b_{1})&(a_{2},b_{2})\\\\ \\end{vmatrix}
ans=∣∣∣∣(a1,b1)(a2,b1)(a1,b2)(a2,b2)∣∣∣∣
(
a
1
,
b
1
)
(a_{1},b_{1})
(a1,b1)表示从(n,0)到(0,m)的路径数,从(n,0)到(0,m)共有n+m步,我们选择其中n步向上走,剩下的自然是向右走,共
C
n
+
m
n
C_{n+m}^{n}
Cn+mn种方法,其他同理
最终答案ans=
C
n
+
m
n
∗
C
n
+
m
n
−
1
−
C
n
+
m
m
−
1
−
C
n
+
m
n
C_{n+m}^{n}*C_{n+m}^{n-1}-C_{n+m}^{m-1}-C_{n+m}^{n}
Cn+mn∗Cn+mn−1−Cn+mm−1−Cn+mn
代码:
#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{
x= 0;
char c= getchar();
bool flag= 0;
while (c < '0' || c > '9')
flag|= (c == '-'), c= getchar();
while (c >= '0' && c <= '9')
x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();
if (flag)
x= -x;
read(Ar...);
}
template <typename T> inline void write(T x)
{
if (x < 0) {
x= ~(x - 1);
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef ONLINE_JUDGE
#else
startTime = clock ();
freopen("data.in", "r", stdin);
#endif
}
void Time_test()
{
#ifdef ONLINE_JUDGE
#else
endTime= clock();
printf("\\nRun Time:%lfs\\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int maxn=3e6+9;
const int mod=1e9+7;
ll inv[maxn];
ll f[maxn];
ll f0[maxn];
void init(int N){
inv[1]=inv[0]=1;
f[1]=f[0]=1;
f0[0]=f0[1]=1;
for(int i=2;i<=N;i++){
f[i]=f[i-1]*i%mod;
f0[i]=(mod-mod/i)*f0[mod%i]%mod;
inv[i]=inv[i-1]*f0[i]%mod;
}
}
ll C(ll a,ll b){
return 1ll*f[a]*inv[b]%mod*inv[a-b]%mod;
}
int main()
{
//rd_test();
init(10000);
ll n,m;
while(~scanf("%lld%lld",&n,&m)){
cout<<(C(n+m,n)*C(n+m,n)%mod-C(n+m,n-1)*C(n+m,m-1)%mod+mod)%mod<<endl;
}
//Time_test();
}
以上是关于2019牛客多校Monotonic Matrix的主要内容,如果未能解决你的问题,请参考以下文章