POJ2826计算几何线段交点

Posted 2021-10-21 hesorchen

题目

An Easy Problem?!

在平面中给出两条线段，问最多能接到多少从上至下的雨水。

解题思路

要能接到雨水，首先得满足两条线段相交形成‘V’型结构，相交大致有以下情况，比较难考虑到的有情况3、4：

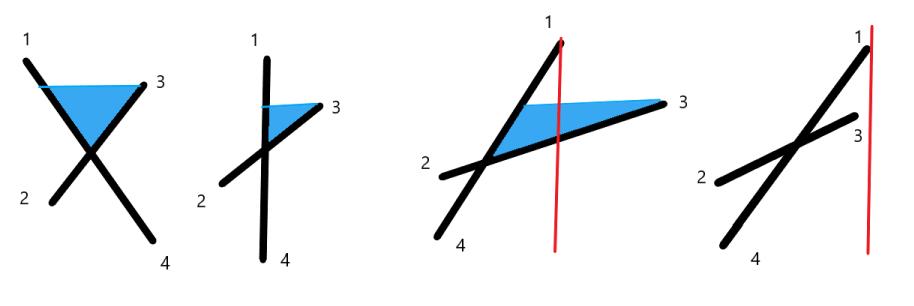
来找四种情况的特征即可。方法很多，下面是一种可行方法

情况2：点1点2的y坐标相同

情况1：过点1作垂线与直线23交于点5，点5的y坐标小于直线14-23的交点坐标。

情况3、4：作点1的垂线交直线23于点5，判断点5点3上方还是下方即可。

判断方法很多，尽量减少运算次数、除法为优。

POJ的老编译CE太难受了，还有经典C++AC，G++WA

代码

#include <iostream>
#include <cmath>
#include <cstdio>
using namespace std;

const int N = 1e5 + 5;
long double x[N], y[N];

const long double eps = 1e-6;

int sign(long double x)
{
    if (fabs(x) <= eps)
        return 0;
    if (x < 0)
        return -1;
    return 1;
}
typedef struct Point
{
    long double x, y;

    Point operator-(const Point &temp) const
    {
        Point T;
        T.x = x - temp.x;
        T.y = y - temp.y;
        return T;
    }
    Point operator+(const Point &temp) const
    {
        Point T;
        T.x = x + temp.x;
        T.y = y + temp.y;
        return T;
    }
    Point operator*(long double k) const
    {
        Point T;
        T.x = k * x;
        T.y = k * y;
        return T;
    }
} Vector;

Point a[7];

long double cross(Vector a, Vector b)
{
    return a.x * b.y - a.y * b.x;
}

long double dot(Vector a, Vector b)
{
    return a.x * b.x + b.x * a.y;
}

long double get_length(Vector a)
{
    return sqrt(dot(a, a));
}

long double get_p0(Point a, Point b)
{
    return get_length(a + b) / 2;
}

Point get_intersection(Point p, Vector v, Point q, Vector w)
{
    Vector u = p - q;
    return p + v * (cross(u, w) / cross(w, v));
}

bool check(Point a1, Point a2, Point a3, Point a4)
{
    Vector v12 = a2 - a1;
    Vector v13 = a3 - a1;
    Vector v14 = a4 - a1;

    Vector v31 = a1 - a3;
    Vector v32 = a2 - a3;
    Vector v34 = a4 - a3;

    if (sign(cross(v12, v14)) * sign(cross(v12, v13)) > 0 || sign(cross(v34, v31)) * sign(cross(v34, v32)) > 0) //线段无交点{
        return 0;
    return 1;
}

void out(Point X, Point A, Point B)
{
    if (A.y < B.y)
        swap(A, B);
    Point B2 = {B.x - 1, B.y};
    Point X2 = get_intersection(A, A - X, B2, B2 - B);
    long double ans = cross(X2 - X, B - X) / 2;
    printf("%.2Lf\\n", fabs(ans));
}
void solve()
{
    for (int i = 1; i <= 4; i++)
        scanf("%Lf %Lf", &a[i].x, &a[i].y);

    if (cross(a[1] - a[2], a[3] - a[4]) == 0) //两线段平行
    {
        printf("0.00\\n");
        return;
    }

    if (!check(a[1], a[2], a[3], a[4])) //两线段不相交
    {
        printf("0.00\\n");
        return;
    }

    Point p1 = a[1];
    Vector v1 = a[2] - a[1];
    Point p2 = a[3];
    Vector v2 = a[4] - a[3];
    Point X = get_intersection(p1, v1, p2, v2); //求出交点

    // cout << "交点 " << X.x << ' ' << X.y << endl;
    Point A, B;
    int flag = 0;
    for (int i = 1; i <= 4; i++)
    {
        if (a[i].y > X.y)
        {
            if (!flag)
                A = a[i];
            else
                B = a[i];
            ++flag;
        }
    }
    if (flag < 2) //要有两个端点的y坐标在交点X之上
    {
        printf("0.00\\n");
        return;
    }

    if (A.x == X.x || B.x == X.x) //有垂直的情况
    {
        out(X, A, B);
        return;
    }

    Point B3 = B;
    B3.y++;
    Point fuck = get_intersection(B, B3 - B, X, X - A); //点B的垂线和XA的交点
    if (fuck.y < X.y)                                   //交点的y坐标小于X的y坐标 说明是情况1
    {
        out(X, A, B);
        return;
    }

    //剩下的就是情况3/4
    if (A.x == B.x)
    {
        printf("0.00\\n");
        return;
    }

    if (fabs(A.x - X.x) > fabs(B.x - X.x))
        swap(A, B); //使A为x坐标更近的那个

    Point A2 = A;
    A2.y -= 1;

    Point woc = get_intersection(A, A2 - A, X, X - B);
    if (woc.y < A.y) //点A的垂线和线段XB的交点 在A下方
        out(X, A, B);
    else
        printf("0.00\\n");
}
int main()
{
    int t;
    cin >> t;
    while (t--)
        solve();

    return 0;
}