POJ - 2826 An Easy Problem?!
Posted 斗奋力努
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了POJ - 2826 An Easy Problem?!相关的知识,希望对你有一定的参考价值。
计算几何好题,神学过题
POJ - 2826 An Easy Problem?!
题意:t组数据。每组数据给你两根棍子,天上会下雨,问两根棍子组成的图形最多可以装多少水
思路:其实要求两根棍子组成的图形,开口向上的可装水三角形的面积
步骤1:
①:特判掉存在有棍子与x轴平行的情况
②:特判掉两根棍子没有交点的情况
③:特判掉两根棍子平行的情况
步骤2:求出两根棍子的交点inter,并找出两根棍子中y值大于交点y值的所有端点cnt,存在dot数组里面
只有y值大于交点y值的才可能做出贡献(0<=cnt<=2)
步骤3:特判掉只有一个端点y值大于交点y值得情况。
步骤4:特殊处理存在一根棍子与y轴平行的情况
①:平行y轴的向量成限制 (图一)
②:斜边成限制 (图二)
步骤5:现在只需要处理交点O(点inter)、端点A(点dot[1])、端点B(点dot[2])三个点所构成可装水三角形的面积
①:保证向量(O->A)到向量(O->B)是逆时针,::(应该是右手螺旋定则
②:保证向量(O->A)与x轴正方向构成的角是锐角。若不是锐角,就根据y轴镜像对称进行变化,变成锐角。
目的:这样只要处理锐角一种情况,方便一点,可以少进行一次讨论
③:向量(O->B)遮住向量(O->A),使无法装水 (图三)
④:向量(O->B)的y值小于等于向量(O->A)的y值,此时向量(O->B)成装水的最后限制。dot[3]代替dot[1] (图四)
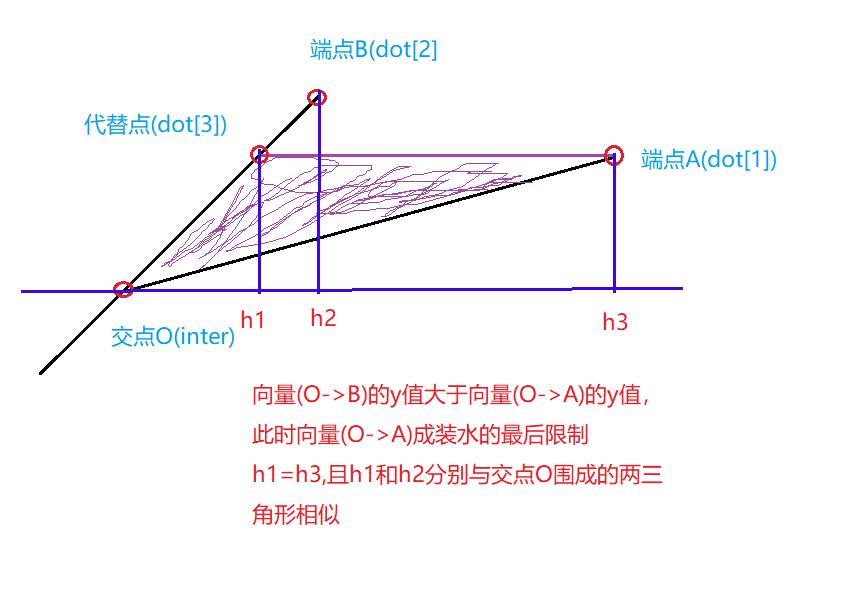
⑤:向量(O->B)的y值大于向量(O->A)的y值,此时向量(O->A)成装水的最后限制。dot[3]代替dot[2](图五)
④⑤求dot[3]是类似相似三角形的求法就行了
④⑤最终面积S就是交点O、(端点dot[1]/端点dot[2])、替代点dot[3]这三个点构成的三角形面积。
面积加上eps就可以ac,加eps可ac属于神学
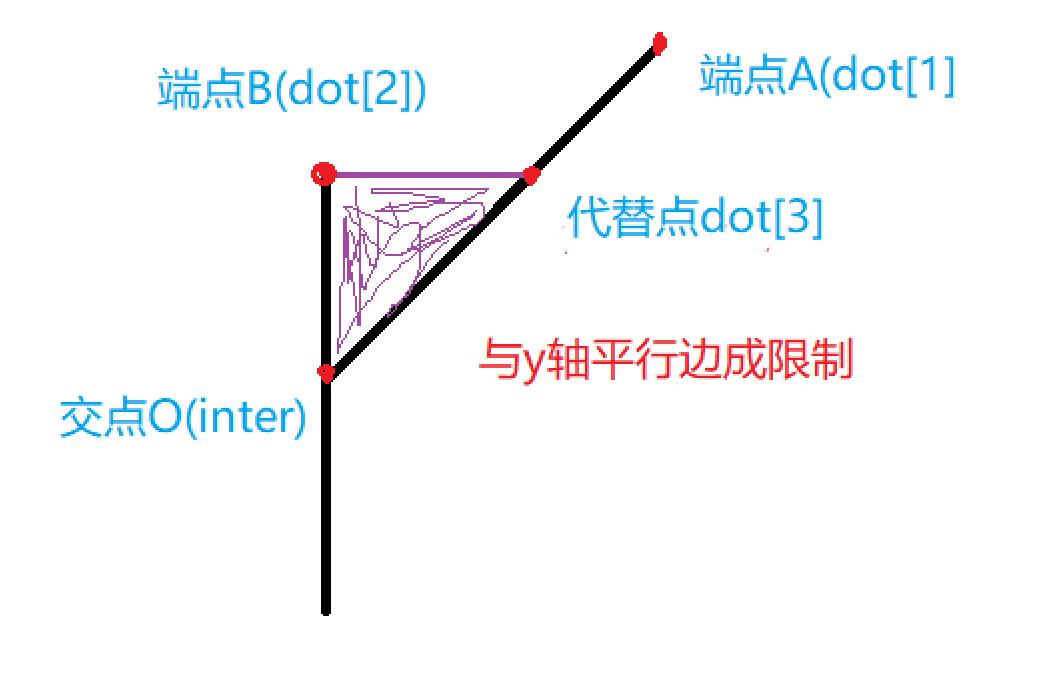 图一
图一
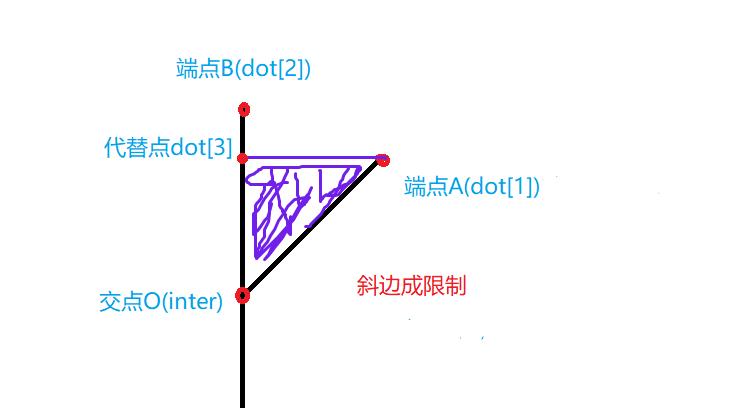 图二
图二
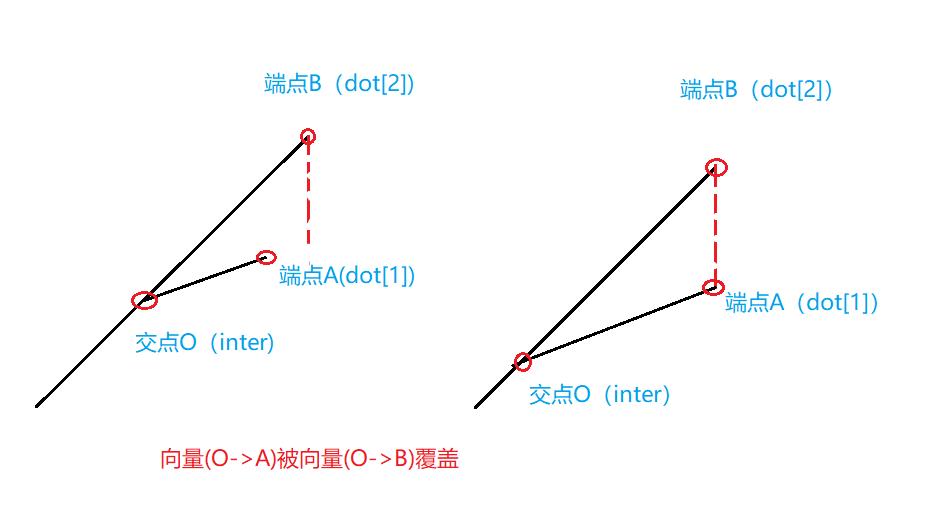 图三
图三
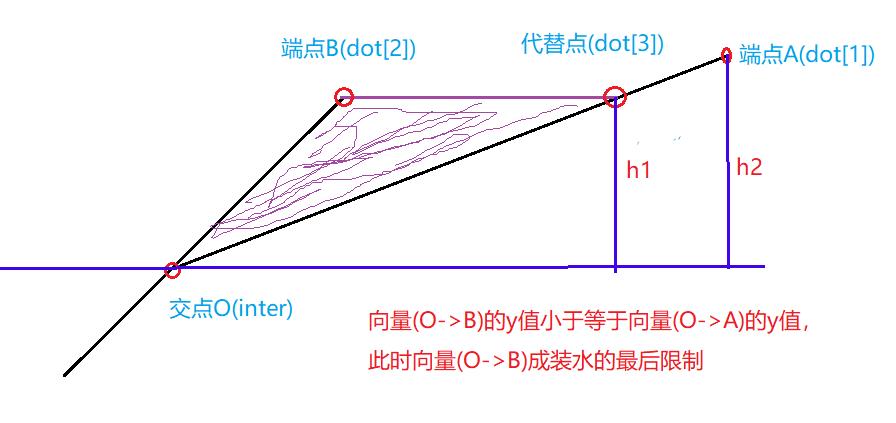 图四
图四
 图五
图五
最后看代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define x first
#define y second
using namespace std;
typedef pair<double,double>PDD;
const double pi=acos(-1);
const double eps=1e-8;
PDD a[10];
PDD operator-(PDD a,PDD b){return {a.x-b.x,a.y-b.y};}
PDD operator+(PDD a,PDD b){return {a.x+b.x,a.y+b.y};}
PDD operator*(PDD a,double b){return {a.x*b,a.y*b};}
double operator*(PDD a,PDD b){return a.x*b.y-a.y*b.x;}
double operator&(PDD a,PDD b){return a.x*b.x+a.y*b.y;}
double area(PDD p,PDD a,PDD b){return (a-p)*(b-p)/2;}
double get_length(PDD a){return sqrt(a&a);}
double get_angle(PDD a,PDD b){//计算向量夹角
return acos((a&b)/get_length(a)/get_length(b));
}
int sign(double x){
if(fabs(x)<eps) return 0;
if(x<0) return -1;
return 1;
}
bool segment_intersection(PDD a1,PDD a2,PDD b1,PDD b2){ //两线段是否有交点
double c1=(a1-a2)*(a1-b1);
double c2=(a1-a2)*(a1-b2);
double c3=(b1-b2)*(b1-a2);
double c4=(b1-b2)*(b1-a1);
return sign(c1)*sign(c2)<=0&&sign(c3)*sign(c4)<=0;
}
PDD get_line_intersection(PDD p,PDD v,PDD q,PDD w){//两直线的交点(点项式)
PDD u=p-q;
double t=(w*u)/(v*w);
return p+v*t;
}
void my_sort(PDD &a,PDD &b){
if(a.y>b.y) swap(a,b);
}
void solve(){
for(int i=1;i<=4;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
my_sort(a[1],a[2]),my_sort(a[3],a[4]);//每根棍子排序,保证前一个端点的y值小就行。可以不加
if(a[1].y==a[2].y||a[3].y==a[4].y) {puts("0.00");return;} //步骤1-①
if(!segment_intersection(a[1],a[2],a[3],a[4])){puts("0.00");return;} //步骤1-②
if(!sign((a[2].y-a[1].y)*(a[4].x-a[3].x)-(a[4].y-a[3].y)*(a[2].x-a[1].x))){puts("0.00");return;} //步骤1-③
PDD inter=get_line_intersection(a[1],a[2]-a[1],a[3],a[4]-a[3]); //步骤2 求交点
PDD dot[5];
int cnt=0;
for(int i=1;i<=4;i++){ //找出y值大于交点y值的端点
if(a[i].y>inter.y){
dot[++cnt]=a[i];
}
}
if(cnt<2) {puts("0.00");return;} //步骤3
if(a[3].x==a[4].x){swap(a[1],a[3]),swap(a[2],a[4]);} //若有与y轴平行的棍子,使是保证是第一根棍子与y轴平行
if(a[1].x==a[2].x){//步骤4
if(dot[1].x!=inter.x) swap(dot[1],dot[2]);
double h,l,S;
if(sign(dot[2].y-dot[1].y)>=0){
h=dot[1].y-inter.y;
double h1=h,h2=dot[2].y-inter.y;
double l2=dot[2].x-inter.x;
l=(h1*l2)/h2;
}
else{
h=dot[2].y-inter.y;
l=dot[2].x-inter.x;
}
S=h*l/2;
printf("%.2f\\n",fabs(S));
}
else{//步骤5
if(sign(area(inter,dot[1],dot[2]))<0) swap(dot[1],dot[2]); //步骤5-①
if(get_angle(dot[1]-inter,{1000,0})*2>pi){//步骤5-②。该if语句为真的唯一情况就是向量(O-A)与x轴正方向夹角为钝角
dot[1].x=-dot[1].x; //根据y轴进行镜像变换
dot[2].x=-dot[2].x;
inter.x=-inter.x; //记得交点也需要
swap(dot[1],dot[2]);
}
if(dot[2].x>=dot[1].x) puts("0.00"); //步骤5-③
else if(dot[2].y<=dot[1].y){//步骤5-④
dot[3].y=dot[2].y;
dot[3].x=((dot[3].y-inter.y)*(dot[1].x-inter.x))/(dot[1].y-inter.y)+inter.x; //相似三角形
double S=(dot[3].y-inter.y)*(dot[3].x-dot[2].x)/2;
printf("%.2f\\n",fabs(S)+eps);
}
else{//步骤5-⑤
dot[3].y=dot[1].y;
dot[3].x=(dot[1].y-inter.y)*(dot[2].x-inter.x)/(dot[2].y-inter.y)+inter.x; //相似三角形
double S=(dot[3].y-inter.y)*(dot[1].x-dot[3].x)/2;
printf("%.2f\\n",fabs(S)+eps);
}
}
}
int main(){
int t;scanf("%d",&t);
while(t--) solve();
}
hack数据
/*
输入
10
6259 2664 8292 9080 1244 2972 9097 9680
0 1 1 0 1 0 2 1
0 1 2 1 1 0 1 2
0 0 10 10 0 0 9 8
0 0 10 10 0 0 8 9
0.9 3.1 4 0 0 3 2 2
0 0 0 2 0 0 -3 2
1 1 1 4 0 0 2 3
1 2 1 4 0 0 2 3
0 0 -10 10 0 0 -3 5
*/
/*
输出
6162.65
1.00
0.00
0.00
4.50
0.50
3.00
0.75
0.00
5.00
*/
以上是关于POJ - 2826 An Easy Problem?!的主要内容,如果未能解决你的问题,请参考以下文章