《剑指Offer——0到n-1中缺失的数字》代码
Posted 穿迷彩服的鲨鱼
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《剑指Offer——0到n-1中缺失的数字》代码相关的知识,希望对你有一定的参考价值。
前言
//==================================================================
// 《剑指Offer——0到n-1中缺失的数字》代码
// 题目:一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字
// 都在范围0到n-1之内。在范围0到n-1的n个数字中有且只有一个数字不在该数组
// 中,请找出这个数字。
//==================================================================
一、示例
示例 1:
输入: [0,1,3]
输出: 2
示例 2:
输入: [0,1,2,3,4,5,6,7,9]
输出: 8
二、代码解析
1.新建.cpp文件
代码如下(示例):
//==================================================================
// 《剑指Offer——0到n-1中缺失的数字》代码
// 题目:一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字
// 都在范围0到n-1之内。在范围0到n-1的n个数字中有且只有一个数字不在该数组
// 中,请找出这个数字。
//==================================================================
#include<iostream>
#include<unordered_map>
#include<vector>
using namespace std;
/*哈希表*/
int missingNumber1(vector<int>& nums)
{
int length = nums.size() + 1;
unordered_map<int, int> map;
for (int num : nums)
{
map[num]++;
}
for (int i = 0; i < length; ++i)
{
map[i]++;
if (map[i] == 1)
{
return i;
}
}
return -1;
}
/*数学计算======公式n*(n-1)/2*/
int missingNumber2(vector<int>& nums)
{
int length = nums.size() + 1;
int L0 = 0;
int L1 = length * (length - 1) / 2;
for (int i = 0; i < length - 1; i++)
{
L0 += nums[i];
}
return L1 - L0;
}
/*二分查找*/
int GetMissingNumber(vector<int>& nums)
{
if (nums.empty())
{
return -1;
}
int left = 0;
int right = nums.size() - 1;
while (left <= right)
{
int middle = (right + left) / 2;
if (nums[middle] != middle)
{
if (middle == 0 || nums[middle - 1] == middle - 1)
{
return middle;
}
else
{
right = middle - 1;
}
}
else
{
left = middle + 1;
}
}
if (left == nums.size())
{
return nums.size();
}
// 无效的输入,比如数组不是按要求排序的,
// 或者有数字不在0到n-1范围之内
return -1;
}
int main()
{
vector<int> nums = { 0,1,2,3,4,5,6,7,9 };
cout << "法一-->哈希表-->" << missingNumber1(nums) << endl;
cout << "法二-->数学计算-->" << missingNumber2(nums) << endl;
cout << "法一-->二分查找-->" << GetMissingNumber(nums) << endl;
return 0;
}
2.测试
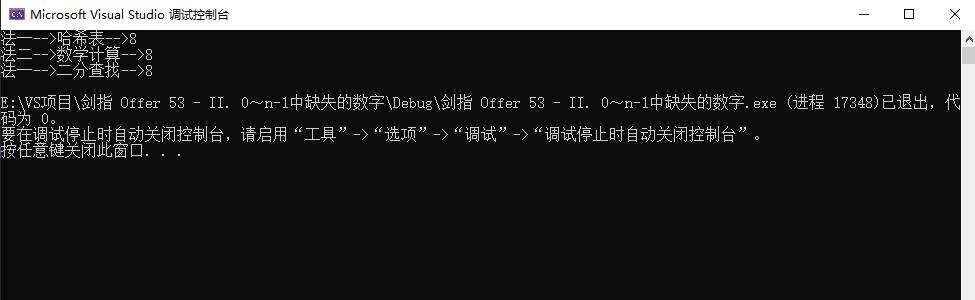
以上是关于《剑指Offer——0到n-1中缺失的数字》代码的主要内容,如果未能解决你的问题,请参考以下文章
剑指Offer面试题53 - II. 0~n-1中缺失的数字