刷算法题总结的一些结论公式

Posted 2021-10-15 辉小歌

根据之前刷过的题还是总结一下结论和模板吧。不然一会儿就又忘完了。
感觉知道一些结论做题是很有帮助的。

目录

• 快速的判断一个大数是不是3的倍数，或9的倍数
• 判断一个字符串是不是回文
• 求n!的约数个数
• 判断是不是润年
• 求n!转化成2进制的位数
• 以知三角形的边求面积
• 约瑟夫环问题
• 俩数互质，最大不可以组合出的数字
• 等比数列，等差数列求和公式
• 求一个数转换成2进制中1的个数
• 大数与大数的乘法
• 一元三次方程求解
• 凸多边形对角线交点的个数
• 平面上有N条直线，最多有几个交点
• 用N个三角形最多可以把平面分成几个区域
• 多重集的排列组合问题
• 求一个数的约数之和。

快速的判断一个大数是不是3的倍数，或9的倍数

将这个数的所有位的数相加，如果mod3等于0就是3的倍数，如果mod9等于0就是9的倍数
详细的推理过程
注意: 这里只适用于 3和9。

bool check9(string s)
{
	int cnt=0;
	for(int i=0;i<s.size();i++) cnt+=s[i]-'0';
	if(cnt%9==0) return true;
	else return false;
}
bool check3(string s)
{
	int cnt=0;
	for(int i=0;i<s.size();i++) cnt+=s[i]-'0';
	if(cnt%3==0) return true;
	else return false;
}

判断一个字符串是不是回文

bool check(string s)
{
	string a=s; reverse(a.begin(),a.end());
	return s==a;
}

求n!的约数个数

一个数约数的个数等于这个数分解质因子后，(每个质数的个数+1）的乘积

typedef long long int LL;
map<LL,LL>mp;
void f(LL  x)
{
    for(int i=2;i<=x/i;i++) while(x%i==0) mp[i]++,x/=i;
    if(x!=1) mp[x]++;
}
LL solve(int n)
{
    LL ans=1;
    for(int i=2;i<=n;i++) f(i);
    for(auto i=mp.begin();i!=mp.end();i++) ans=ans*(i->second+1);
    return ans;
}

判断是不是润年

bool judge(int year)
{
	if(year%400==0|| (year%4==0&&year%100!=0) ) return true;
	else return false;
}

求n!转化成2进制的位数

LL solve(int n)
{
	double sum=0;
	for(int i=1;i<=n;i++) sum+=log2(i);
	return sum+1;
}

以知三角形的边求面积

double solve(int a,int b,int c)
{
	double p=(a+b+c)/2;
	return sqrt(p*(p-a)*(p-b)*(p-c));
}

约瑟夫环问题

公式推理

int solve(int n,int k)//1到n个人,报到k的最后留下来的编号
{
	int ans=0;
	for(int i=2;i<=n;i++) ans=(ans+k)%i;
	return ans+1;
}

俩数互质，最大不可以组合出的数字

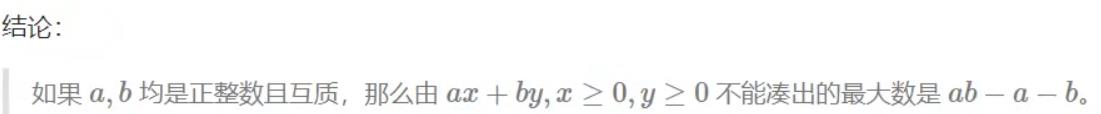
ab-a-b==(a-1)*(b-1)-1

int solve(int a,int b){return (a-1)*(b-1)-1;}

等比数列，等差数列求和公式

求一个数转换成2进制中1的个数

int lowbit(int x){return x&-x;}
int solve(int x)//输入一个数x
{
	int cnt=0;
	while(x) x-=lowbit(x),cnt++;
	return cnt;
}

大数与大数的乘法

vector<int> mul(vector<int> &A,vector<int> &B)
{
	int t=0; vector<int> C;
	C.push_back(0);//目的是容器里初始化
	for(int j=0;j<B.size();j++)
	{
		for(int i=0;i<A.size();i++)
		{
			C.push_back(0);
			C[i+j]+=A[i]*B[j];
		}
	}
	for(int i=0;i<C.size();i++)//处理进位
	{
		if(C[i]>=10)
		C[i+1]+=C[i]/10,C[i]=C[i]%10;
	} 
	while(C.size()>1&&C.back()==0) C.pop_back();//处理前导零
	return C;
}

一元三次方程求解

void solve(double a,double b,double c,double d)//只适用于三个解互相不通的情况。
{
	double A,B,C,T,ac,x1,x2,x3;
	A=b*b-3*a*c;          
	B=b*c-9*a*d;          
	T=(2*A*b-3*a*B)/(2*sqrt(A*A*A));          
	ac=acos(T);          
	x1=(-b-sqrt(A)*cos(ac/3)*2)/3/a;          
	x2=(-b+sqrt(A)*(cos(ac/3)-sqrt(3)*sin(ac/3)))/(3*a);          
    x3=(-b+sqrt(A)*(cos(ac/3)+sqrt(3)*sin(ac/3)))/(3*a);      
    printf("%.2lf %.2lf %.2lf",x1,x2,x3);
}

凸多边形对角线交点的个数

首先一个交点对应两条对角线，二这两条对角线是有四个点确定的。
所以只要求$C_n^4$就可以了 即 n(n-1)(n-2)(n-3)/24

typedef  unsigned long long int LL;
LL solve(LL x){return x*(x-1)/2*(x-2)/3*(x-3)/4;}

平面上有N条直线，最多有几个交点

俩线一个点，共 $C_n^2$个点

int solve(int x){return x*(x-1)/2;}

用N个三角形最多可以把平面分成几个区域

f[i]=f[i-1]+6*(i-1)
推导

LL f[100005];
LL solve(int n)
{
	f[1]=2;
	for(int i=2;i<=n;i++) f[i]=f[i-1]+6*(i-1);
	return f[n];
}

多重集的排列组合问题

实战题目: 猴子排序的期望 ， 擅长解密的小红同学

求一个数的约数之和。

typedef long long int LL;
const int mod=1e9+7;
map<LL,LL>mp;
void f(int x)
{
    for(int i=2;i<=x/i;i++) while(x%i==0) mp[i]++,x/=i;
    if(x!=1) mp[x]++;
}
LL solve()
{
    LL ans=1;
    for(auto i=mp.begin();i!=mp.end();i++)
    {
        LL temp=1;
        int m=i->second;
        LL a=i->first;
        for(int j=1;j<=m;j++) temp=(temp*a+1)%mod;
        ans=(ans*temp)%mod;
    }
    return ans;
}