贝叶斯定理简单理解
Posted ZhangJiQun.
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了贝叶斯定理简单理解相关的知识，希望对你有一定的参考价值。
目录
先验概率是在缺乏某个事实的情况下描述一个变量;
后验概率是在考虑了一个事实之后的条件概率;
频率概率的计算公式，你可以轻松的知道中奖的概率=中奖球数（2个白球）/球总数（2个白球+8个黑球）=2/10
频率概率的计算公式，你可以轻松的知道中奖的概率=中奖球数（2个白球）/球总数（2个白球+8个黑球）=2/10
1）要求解的问题：女神喜欢你，记为A事件
2）已知条件：女神经常冲你笑，记为B事件
1）先验概率
我们把P(A)称为"先验概率"（Prior probability），也就是在不知道B事件的前提下，我们对A事件概率的一个主观判断。
对应这个例子里就是在不知道女神经常对你笑的前提下，来主观判断出女神喜欢一个人的概率。这里我们假设是50%，也就是不喜欢你，可能不喜欢你的概率都是一半。
2）可能性函数
P(B|A)/P(B)称为"可能性函数"（Likelyhood），这是一个调整因子，也就是新信息B带来的调整，作用是将先验概率（之前的主观判断）调整到更接近真实概率。
可能性函数你可以理解为新信息过来后，对先验概率的一个调整。
如果"可能性函数"P(B|A)/P(B)>1，意味着"先验概率"被增强，事件A的发生的可能性变大；如果"可能性函数"=1，意味着B事件无助于判断事件A的可能性；如果"可能性函数"<1，意味着"先验概率"被削弱，事件A的可能性变小。
还是刚才的例子，根据女神经常冲你笑这个新的信息，我调查走访了女神的闺蜜，最后发现女神平日比较高冷，很少对人笑，也就是对你有好感的可能性比较大（可能性函数>1）。所以我估计出"可能性函数"P(B|A)/P(B)=1.5（通过以往数据得知）
3）后验概率
P(A|B)称为"后验概率"（Posterior probability），即在B事件发生之后，我们对A事件概率的重新评估。这个例子里就是在女神冲你笑后，对女神喜欢你的概率重新预测。
带入贝叶斯公式计算出P(A|B)=P(A)* P(B|A)/P(B)=50% *1.5=75%
先验概率
条件概率
由于堵车造成迟到的原因
条件概率：硬币自由正反两面（常识）；
后验概率
全概率公式
求迟到原因的概率（堵车造成，拉肚子造成，有事情造成）
堵车造成迟到概率
B：迟到 A:堵车
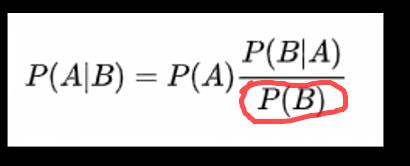
总结：
我迟到的原因只可能是堵车、闹钟坏了、拉肚子三种情况中的一种，且这三种情况不可能同时发生，那么我今天如果又迟到了，造成的原因是什么的概率最大呢？
这个问题已经无法用抛硬币来进行解决了，因为传统频率主义是无法解决实际问题的
换言之抛硬币问题只存在于理论中，实际生活中某个事件的发生条件或结果一定是复杂的
比如迟到这个事件，我们已经知道了引起迟到的所有条件，且这些条件都是相互独立且互斥的
那么想要求出迟到的概率，就可以将这个复杂事件拆分成几个条件概率，比如迟到的概率可以拆分成：
=P（堵车且迟到）+P（闹钟坏了且迟到）+P（拉肚子且迟到）=P（堵车）*P（迟到 | 堵车）+P（闹钟坏了）*P（迟到 | 闹钟坏了）+P（拉肚子）*P（迟到 | 拉肚子）
如果有多个事件，就可以用公式这么进行表达：
这就是全概率公式，简单来说就是用来进行复杂事件概率求算的。
那么回到问题，想要求哪个原因造成的迟到概率最大，比如先求迟到的原因概率，就可以根据条件概率和全概率进行推导：
=P（堵车且迟到）/ P（迟到）=P（堵车）*（迟到 | 堵车） / P（堵车）*P（迟到 | 堵车）+P（闹钟坏了）*P（迟到 | 闹钟坏了）+P（拉肚子）*P（迟到 | 拉肚子）
用公式表达就是
如果你看到这里，那么恭喜你你已经成功推导出了贝叶斯定理的公式
其中不难发生，这个公式的分母其实就是全概率公式，也就是P（B），所以贝叶斯公式又可以写成下面这个形式：
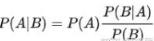
其核心思想是当你不能准确知悉一个事物的本质时，你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。
举例
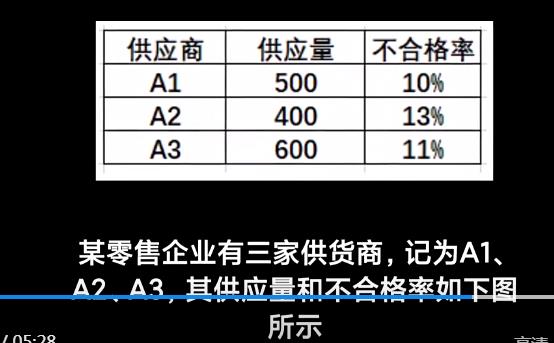
计算抽取不合格产品概率
11.2%：B事件
问题：抽到产品不合格来源于谁
贝叶斯计算公式
最终化成百分制；
=29.8%
贝叶斯定理
结合开车来理解贝叶斯公式
我们来看看贝叶斯公式是怎么写的：
如果我们知道，在整个车辆行驶过程中，会有 的概率打右转弯灯，即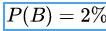 
，我们就可以计算 
了。
因此贝叶斯就是：
韦恩图
又称文氏图，是一种简单的图形，也是科研文章中最常见的图，可以用来表示多个数据集的大致之间的关系。当然也可以进行集合运算。绘制韦恩图的工具有很多，在此，小编总结了几种常用简单的在线绘制韦恩图的在线的工具.
我们可以看到有形的十字路口，却看不到明天是否下雨，我们可以看到前方是否有路障，却不清楚下一次飞机是否会出事。甚至有时候，眼睛还会欺骗我们。
很多时候，我们不得不看着后视镜开车，这个时候概率论、贝叶斯定理就是我们的指路明灯。
看着后视镜开车，肯定常常会撞车，没关系，我们可以不断的去修正我们的假设。
比如，撞了几次车之后，就发现可能之前估计的在十字路口打右转弯灯的数据明显偏大了，我们修正之后再继续开车。我们人类的学习，本身也是一个试错的过程。
贝叶斯定理现在很多人在研究，就是因为不少人相信贝叶斯定理和人脑的工作机制很像，因此成为机器学习的基础。
比如，你和对方聊天的时候，如果对方说出我们的大脑看起来就好像是天生在用贝叶斯定理。“虽然”两个字，你大概就会猜测，对方后继九成的可能性会说出“但是”。
后来，google由自然语言处理专家贾里尼克领导的部门，通过统计、概率方法进行上述研究，正确率提高了很多。在书中也列举了贝叶斯定理是如何参与自然语言处理的。
语法是人类后来总结出来的，我们天生是不需要语法就可以开口说话的，或许，人脑真的是贝叶斯大脑。
贝叶斯分类
贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。
分类问题综述
对于分类问题，其实谁都不会陌生，日常生活中我们每天都进行着分类过程。例如，当你看到一个人，你的脑子下意识判断他是学生还是社会上的人；你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱、”之类的话，其实这就是一种分类操作。
既然是贝叶斯分类算法，那么分类的数学描述又是什么呢？
从数学角度来说，分类问题可做如下定义：已知集合
其中C叫做类别集合，其中每一个元素是一个类别，而I叫做项集合（特征集合），其中每一个元素是一个待分类项，f叫做分类器。分类算法的任务就是构造分类器f。
分类算法的内容是要求给定特征，让我们得出类别，这也是所有分类问题的关键。那么如何由指定特征，得到我们最终的类别，也是我们下面要讲的，每一个不同的分类算法，对应着不同的核心思想。
朴素贝叶斯分类
那么既然是朴素贝叶斯分类算法，它的核心算法又是什么呢？
是下面这个贝叶斯公式：
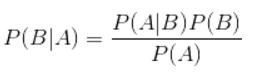
换个表达形式就会明朗很多，如下：最简单通俗的解释，贝叶斯定理是什么？ - 知乎
我们最终求的p(类别|特征)即可！就相当于完成了我们的任务。
朴素贝叶斯分类的优缺点
优点：
（1） 算法逻辑简单,易于实现
（2）分类过程中时空开销小
缺点：
理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。
而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
以上是关于贝叶斯定理简单理解的主要内容，如果未能解决你的问题，请参考以下文章