基于R和Python的极大似然估计的牛顿法实现
Posted 张乃晟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于R和Python的极大似然估计的牛顿法实现相关的知识,希望对你有一定的参考价值。
目录
0.前言
最近在学习Theory and Method of Statistics(统计理论方法),使用的教材是由Bradley Efron 、Trevor Hastie共同编写的Computer Age Statistical Inference: Algorithms, Evidence, and Data Science(《计算机时代的统计推断:算法、演化和数据科学》)。书中第四章讲述的Fisherian Inference and Maximum Likelihood Estimation(费雪推断和极大似然估计),其中提到现实应用中极大似然估计并没有那么容易求解,比如Cauchy分布和Gamma分布。
如果极大似然估计方法没有显式解,可以考虑用数值计算的方法求解(如牛顿法);更进一步,如果二阶导不存在或Hessian矩阵非正定,可以使用拟牛顿法;再复杂一些,可以使用MM算法(EM是MM的特例) 。本文以牛顿法为例,给出求解 Cauchy分布、Gamma分布的极大似然估计参数的理论并使用R和Python实现。
1.理论基础
本节给出牛顿法求分布的极大似然参数估计的一般理论。
如果随机变量 独立同分布于
独立同分布于 ,且已知一组样本
,且已知一组样本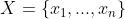 ,为了估计该分布的参数,可以使用极大似然估计的方法。
,为了估计该分布的参数,可以使用极大似然估计的方法。
首先写出样本的似然函数
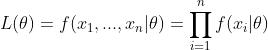
对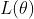 进行对数化处理,得到对数似然函数
进行对数化处理,得到对数似然函数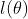

则求解未知参数 等价于求解以下等式方程组
等价于求解以下等式方程组
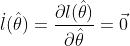
不妨假设收敛解为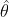 ,将
,将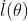 在
在 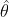 的邻域内展开成泰勒级数得
的邻域内展开成泰勒级数得



这样就得到一个迭代关系式

如果是连续的,并且待求的零点是孤立的,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果不为0, 那么牛顿法将具有平方收敛的性能。 粗略地说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
2.Cauchy分布的极大似然估计
如果随机变量 服从柯西分布,记为
服从柯西分布,记为 ,其中
,其中 为最大值一半处的一半宽度的尺度参数(scale parameter ),
为最大值一半处的一半宽度的尺度参数(scale parameter ), 为定义分布峰值位置的位置参数(location parameter )
为定义分布峰值位置的位置参数(location parameter )

当 ,此时的Cauchy 分布称为标准Cauchy 分布
,此时的Cauchy 分布称为标准Cauchy 分布

Cauchy 分布的最特别的性质是其期望及高阶矩都不存在,自然也就无法对参数进行矩估计。但Cauchy分布的cdf具有很好的性质,可以利用一组样本的分位点来对参数进行点估计。

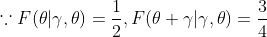

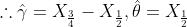
2.1理论基础
使用极大似然方法估计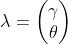 ,已知样本
,已知样本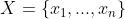
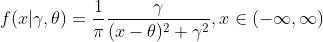

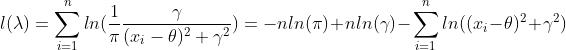


故迭代公式为

2.2算法
Step0:给定 ,
, ,停止精度
,停止精度
Step1:计算 ,如果
,如果
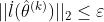
则终止,否则进行下一步
Step2:计算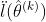 ,令
,令

Step3:计算 , 跳转Step1
, 跳转Step1
2.2.1R语言实现
# 设立牛顿算法框架
Newtons = function(fun, x, theta,ep = 1e-5, it_max = 100){
index = 0 ;k = 1
while (k <= it_max){
theta1 = theta
obj = fun(x,theta)
theta = theta - solve(obj$J,obj$f)
norm = sqrt((theta - theta1) %*% (theta - theta1))
if (norm < ep){
index = 1; break
}
k = k + 1
}
obj = fun(x,theta)
list(root = theta, it = k, index = index, FunVal = obj$f)
}
# 计算hessian矩阵和一阶导数
funs = function(x,theta){
n = length(x)
temp_1 = (x-theta[2])^2+theta[1]^2
temp_2 = (x-theta[2])^2-theta[1]^2
f = c(n/theta[1]-sum(2*theta[1]/temp_1),
sum((2*(x-theta[2]))/temp_1))
J = matrix(c(-n/theta[1]^2-sum(2*temp_2/temp_1^2), -sum((4*theta[1]*(x-theta[2]))/temp_1^2),
-sum((4*theta[1]*(x-theta[2]))/temp_1^2),sum(2*temp_2/temp_1^2)), nrow = 2, byrow = T)
list(f = f, J = J)
}
# 抽取1000个样本
set.seed(80)
sample = rcauchy(1000,scale = 2,location = 2)
# 计算cauchy分布参数的分位数估计作为初始值
gamma_ = quantile(sample,0.75) - median(sample)
theta_ = median(sample)
theta = c(gamma_,theta_)
Newtons(funs,sample,theta)2.2.2Python语言实现
import numpy as np
import scipy.stats as st
np.random.seed(12)
sample = st.cauchy.rvs(loc=1,scale = 1,size = 100) # scipy.stats.cauchy.rvs(loc=0, scale=1, size=1, random_state=None)
gamma_ = np.quantile(sample,0.75) - np.median(sample)
theta_ = np.median(sample)
theta = np.array([gamma_,theta_])
def Newtons(fun,x,theta,ep=1e-5,it_max = 100):
index = 0
k = 1
while k <= it_max:
theta1 = theta
obj = fun(x,theta)
theta = theta - np.dot(np.linalg.inv(obj[1]),obj[0])
norm = np.sqrt(np.sum((theta - theta1)**2))
if norm < ep:
index = 1
break
k = k+1
obj = fun(x,theta)
print('gamma,theta估计值为%.3f,%.3f'%(theta[0],theta[1]))
def funs(x,theta):
n = len(x)
temp_1 = (x - theta[1]) ** 2 + theta[0] ** 2
temp_2 = (x - theta[1]) ** 2 - theta[0] ** 2
f = np.array([n/theta[0]-np.sum(2*theta[0]/temp_1),
np.sum((2*(x-theta[1]))/temp_1)])
j = np.array([[-n/theta[0]**2-sum(2*temp_2/temp_1**2),-np.sum((4*theta[0]*(x-theta[1]))/temp_1**2)],
[-np.sum((4*theta[0]*(x-theta[1]))/temp_1**2),sum(2*temp_2/temp_1**2)]])
return [f,j]
Newtons(funs,sample,theta)3.Gamma 分布的极大似然估计
如果随机变量 服从Gamma分布,记为
服从Gamma分布,记为 ,其中
,其中 为形状参数(shape parameter),β 为尺度参数(scale parameter ),λ 为位置参数(location parameter)
为形状参数(shape parameter),β 为尺度参数(scale parameter ),λ 为位置参数(location parameter)

为了给出Gamma分布三个参数的矩估计,现考虑分布的一二三阶原点矩(求解的技巧在于凑Gamma函数)
以一阶原点矩的证明为例,将x拆分为

故
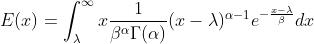

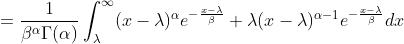
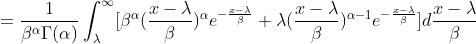
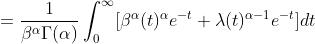
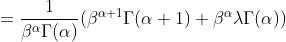
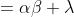 ①
①
对于二阶三阶原点矩,分别将 拆分为
拆分为


易得


又
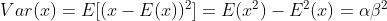 ②
②
 ③
③
由①②③可得

3.1理论基础
已知样本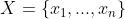 ,参数
,参数




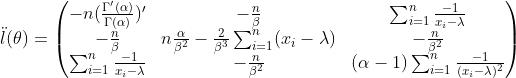
故迭代公式为

3.2算法
Step0:给定 ,
, ,停止精度
,停止精度
Step1:计算 ,如果
,如果
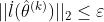
则终止,否则进行下一步
Step2:计算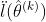 ,令
,令

Step3:计算 , 跳转Step1
, 跳转Step1
3.2.1R语言实现
# 设立牛顿算法框架
Newtons = function(fun, x, theta,ep = 1e-5, it_max = 100){
index = 0; k = 1
while (k <= it_max ){
theta1 = theta; obj = fun(x,theta)
theta = theta - solve(obj$J,obj$f)
norm = sqrt((theta - theta1) %*% (theta - theta1))
if (norm < ep){
index = 1; break
}
k = k + 1
}
obj = fun(x,theta)
list(root = theta, it = k, index = index, FunVal = obj$f)
}
# 计算hessian矩阵和一阶导数
funs = function(x,theta){
n = length(x)
f = c(-n*log(theta[2])-n*digamma(theta[1])+sum(log(x-theta[3])),
-n*theta[1]/theta[2]+1/(theta[2]^2)*sum(x-theta[3]),
(theta[1]-1)*sum(-1/(x-theta[3]))+n/theta[2])
J = matrix(c(-n*trigamma(theta[1]), -n/theta[2], sum(-1/(x-theta[3])),
-n/theta[2],n*theta[1]/(theta[2]^2)-2/(theta[2]^3)*sum(x-theta[3]),-n/(theta[2]^2),
sum(-1/(x-theta[3])),-n/(theta[2]^2),(theta[1]-1)*sum(-1/(x-theta[3])^2)), nrow = 3, byrow = T)
list(f = f, J = J)
}
# 抽取随机gamma
set.seed(80)
sample = rgamma(100,2,)
# 计算gamma分布参数的矩估计作为初始值
s_m = mean(sample)
s_v = var(sample)
m_3 = (sum((sample-s_m)^3))/length(sample)
alpha = (4*(s_v)^3)/(m_3^2)
beta = m_3/(2*s_v)
lambda = s_m-2*((s_v)^2/m_3)
theta = c(alpha,beta,lambda)
Newtons(funs,sample,theta)
3.2.2Python语言实现
import numpy as np
import scipy.stats as st
import scipy.special as sp
np.random.seed(12)
sample = st.gamma.rvs(2,scale = 1,size = 50) # scipy.stats.gamma.rvs(a, loc=0, scale=1, size=1, random_state=None)
s_m = sample.mean()
s_v =sample.var()
m_3 = np.mean(((sample - s_m)**3))
alpha = (4*(s_v)**3)/(m_3**2)
beta = m_3/(2*s_v)
lambda_ = s_m-2*((s_v)**2/m_3)
theta = np.array([alpha,beta,lambda_])
def Newtons(fun,x,theta,ep=1e-5,it_max = 100):
index = 0
k = 1
while k <= it_max:
theta1 = theta
obj = fun(x,theta)
theta = theta - np.dot(np.linalg.inv(obj[1]),obj[0])
norm = np.sqrt(np.sum((theta - theta1)**2))
if norm < ep:
index = 1
break
k = k+1
obj = fun(x,theta)
print('alpha,beta,lambda估计值为%.3f,%.3f,%.3f'%(theta[0],theta[1],theta[2]))
def funs(x,theta):
n = len(x)
f = np.array([-n*np.log(theta[1])-n*sp.digamma(theta[0])+np.sum(np.log(x-theta[2])),
-n*theta[0]/theta[1]+1/(theta[1]**2)*np.sum(x-theta[2]),
(theta[0]-1)*np.sum(-1.0/(x-theta[2]))+n/theta[1]])
j = np.array([[-n*sp.polygamma(1,theta[0]),-n/theta[1],np.sum(-1/(x-theta[2]))],
[-n/theta[1],n*theta[0]/(theta[1]**2)-2/(theta[1]**3)*np.sum(x-theta[2]),-n/(theta[1]**2)],
[np.sum(-1/(x-theta[2])),-n/(theta[1]**2),(theta[0]-1)*np.sum(-1/(x-theta[2])**2)]])
return [f,j]
Newtons(funs,sample,theta)注意:对Gamma分布三参数的极大似然估计过程中,如果使用牛顿法,很容易出现矩阵不正定的情况从而无法得到正确解,这个时候需要寻求其他方法。
以上是关于基于R和Python的极大似然估计的牛顿法实现的主要内容,如果未能解决你的问题,请参考以下文章
