CF1253E Antenna Coverage

Posted 2021-10-07 Jozky86

CF1253E Antenna Coverage

题意：

现在有n个点，每个点的坐标为xi，以及一个范围值si，可以覆盖左右范围[xi-si,xi+si]
每次操作，可以花费代价1让第i个天线的si增加1，每个天线都可以进行多次操作。现在请问你最少需要花费多少代码，使得[1,m]内每个位置都被至少一个天线覆盖

题解：

参考题解
很奇妙的思路
我们设f[i]表示[1,i]被全部覆盖的最小花费，答案为$f_m$
首先引入一个新的点，坐标为0，这样f的初始值就是f[i]=i
这个点很重要，其保证了$f_{i+1}<=f_i+1$，f是单调上升的，且该点的引入并未影响答案，因为我们最后的答案是f[n]，而在最左侧加入一个点，f[n]=n相当于是最差情况，所以不会影响答案
然后我们可以进行转移：
对于点i，我们找在i前面的区间[l,r]，（r要小于i），此时r要扩展x=i-r[]才能覆盖i，l也要扩展x，那么i就可以通过坐标j-1=l-x-1来更新
如图

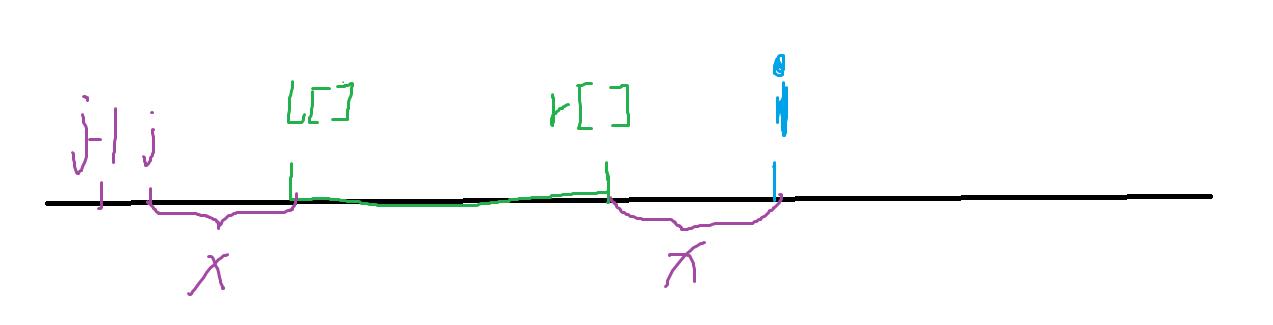
正确性证明可以看参考题解

代码：

#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{
    x= 0;
    char c= getchar();
    bool flag= 0;
    while (c < '0' || c > '9')
        flag|= (c == '-'), c= getchar();
    while (c >= '0' && c <= '9')
        x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();
    if (flag)
        x= -x;
    read(Ar...);
}
template <typename T> inline void write(T x)
{
    if (x < 0) {
        x= ~(x - 1);
        putchar('-');
    }
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef ONLINE_JUDGE
#else
    startTime = clock ();
    freopen("data.in", "r", stdin);
#endif
}
void Time_test()
{
#ifdef ONLINE_JUDGE
#else
    endTime= clock();
    printf("\\nRun Time:%lfs\\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int maxn=100;
struct node{
	int x,s;
}a[maxn];
int f[200004];
int l[maxn];
int r[maxn];
int main()
{
//    rd_test();
	int n,m;
	read(n,m);
	for(int i=1;i<=n;i++){
		read(a[i].x,a[i].s);
		l[i]=a[i].x-a[i].s; 
		r[i]=a[i].x+a[i].s;
	}
	for(int i=1;i<=m;i++)f[i]=i;
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=n;j++){
			if(l[j]<=i&&i<=r[j]){
				f[i]=f[i-1];
				break;
			}
			if(r[j]<i){
				int x=i-r[j];
				f[i]=min(f[max(0,l[j]-x-1)]+x,f[i]);
			}
		}
	}
	cout<<f[m];
    //Time_test();
}