☀️机器学习入门☀️ PCA 和 LDA 降维算法 | 附加小练习(文末送书)
Posted 小生凡一
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了☀️机器学习入门☀️ PCA 和 LDA 降维算法 | 附加小练习(文末送书)相关的知识,希望对你有一定的参考价值。
- 🎉粉丝福利送书:《人工智能数学基础》
- 🎉点赞 👍 收藏 ⭐留言 📝 即可参与抽奖送书
- 🎉下周三(9月22日)晚上20:00将会在【点赞区和评论区】抽一位粉丝送这本书~🙉
- 🎉详情请看第三点的介绍嗷~✨
目录
1. PCA 主成分分析
1.1 算法简介
数据样本虽然是
高维的,但是与学习任务紧密相关的或许仅仅是一个低维嵌入,因此可以对数据进行有效的降维。
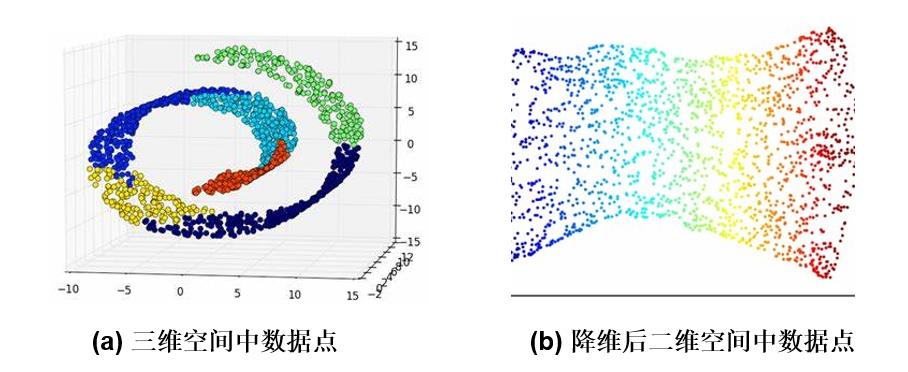
主成分分析是一种统计分析、简化数据集的方法。
它利用
正交变换来对一系列可能相关的变量的观测值进行线性变换,从而投影为一系列线性不相关变量的值,这些不相关变量称为主成分。
1.2 实现思路
一般来说,欲获得低维子空间,最简单的是对原始高维空间进行
线性变换。给定𝒎维空间中的数据点,将其投影到低维空间中,同时尽可能多地保留信息。
- 数据在低维线性空间的正交投影
最大化投影数据的方差(紫色线)。 最小化数据点与投影之间的均方距离(蓝色线之和)。
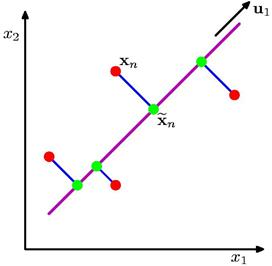
-
主成分概念:
- 主成分分析
(PCA)的思想是将𝒎维特征映射到𝒌维上(𝒌<𝒎),这𝒌维是全新的正交特征。 - 这
𝒌维特征称为主成分(PC),是重新构造出来的𝒌维特征。
- 主成分分析
-
主成分特点:
- 源于质心的矢量。
- 主成分#1指向最大方差的方向。
- 各后续主成分与前一主成分正交,且指向残差子空间最大方差的方向
1.3 公式推算
1.3.1 PCA顺序排序
给定中心化的数据{𝒙_𝟏,𝒙_𝟐,⋯,𝒙_𝒎},计算主向量:
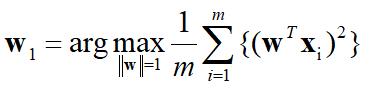
我们最大化𝒙的投影方差
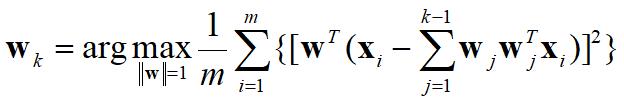
我们使残差子空间中投影的方差最大
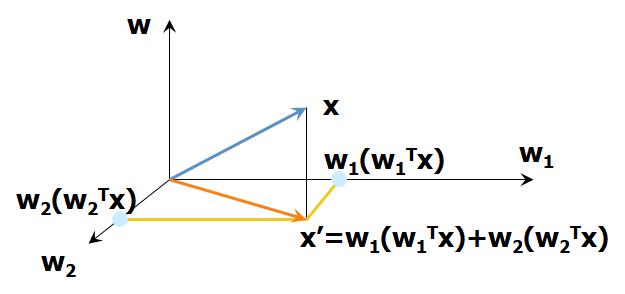
1.3.2 样本协方差矩阵
给定数据{𝒙_𝟏,𝒙_𝟐,⋯,𝒙_𝒎}, 计算协方差矩阵


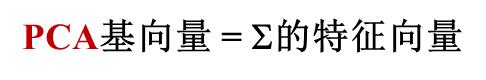


证明不写了,太多公式了,自行百度吧。
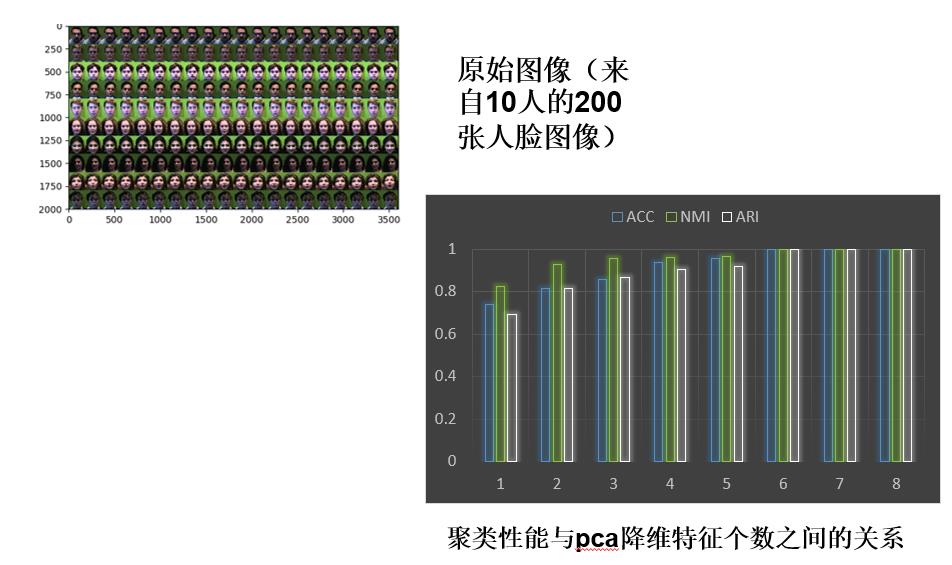
1.4 小练习
给定的图像数据集,探讨pca降维后特征个数与聚类性能的关系。
from PIL import Image
import numpy as np
import os
from ex1.clustering_performance import clusteringMetrics
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
def getImage(path):
images = []
for root, dirs, files in os.walk(path):
if len(dirs) == 0:
images.append([root + "\\\\" + x for x in files])
return images
# 加载图片
images_files = getImage('face_images')
y = []
all_imgs = []
for i in range(len(images_files)):
y.append(i)
imgs = []
for j in range(len(images_files[i])):
img = np.array(Image.open(images_files[i][j]).convert("L")) # 灰度
# img = np.array(Image.open(images_files[i][j])) #RGB
imgs.append(img)
all_imgs.append(imgs)
# 可视化图片
w, h = 180, 200
pic_all = np.zeros((h * 10, w * 10)) # gray
for i in range(10):
for j in range(10):
pic_all[i * h:(i + 1) * h, j * w:(j + 1) * w] = all_imgs[i][j]
pic_all = np.uint8(pic_all)
pic_all = Image.fromarray(pic_all)
pic_all.show()
# 构造输入X
label = []
X = []
for i in range(len(all_imgs)):
for j in all_imgs[i]:
label.append(i)
# temp = j.reshape(h * w, 3) #RGB
temp = j.reshape(h * w) # GRAY
X.append(temp)
def keams_in(X_Data, k):
kMeans1 = KMeans(k)
y_p = kMeans1.fit_predict(X_Data)
ACC, NMI, ARI = clusteringMetrics(label, y_p)
t = "ACC:{},NMI:{:.4f},ARI:{:.4f}".format(ACC, NMI, ARI)
print(t)
return ACC, NMI, ARI
# PCA
def pca(X_Data, n_component, height, weight):
X_Data = np.array(X_Data)
pca1 = PCA(n_component)
pca1.fit(X_Data)
faces = pca1.components_
faces = faces.reshape(n_component, height, weight)
X_t = pca1.transform(X_Data)
return faces, X_t
def draw(n_component, faces):
plt.figure(figsize=(10, 4))
plt.subplots_adjust(hspace=0, wspace=0)
for i in range(n_component):
plt.subplot(2, 5, i + 1)
plt.imshow(faces[i], cmap='gray')
plt.title(i + 1)
plt.xticks(())
plt.yticks(())
plt.show()
score = []
for i in range(10):
_, X_trans = pca(X, i + 1, h, w)
acc, nmi, ari = keams_in(X_trans, 10)
score.append([acc, nmi, ari])
score = np.array(score)
bar_width = 0.25
x = np.arange(1, 11)
plt.bar(x, score[:, 0], bar_width, align="center", color="orange", label="ACC", alpha=0.5)
plt.bar(x + bar_width, score[:, 1], bar_width, color="blue", align="center", label="NMI", alpha=0.5)
plt.bar(x + bar_width*2, score[:, 2], bar_width, color="red", align="center", label="ARI", alpha=0.5)
plt.xlabel("n_component")
plt.ylabel("精度")
plt.legend()
plt.show()
2. LDA 线性判断分析
2.1 算法简介
当我们映射的时候,由于映射的位置不同,所以我们会有不同的降维后的结果。对于下面两个,我们可以看出方法2的分类更明显,方法2是更好的。
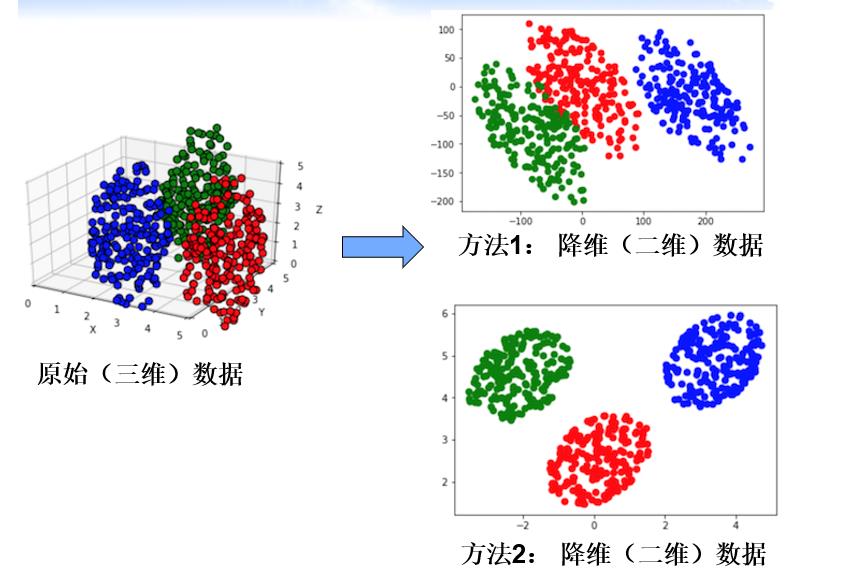 和
和PCA的映射对比。
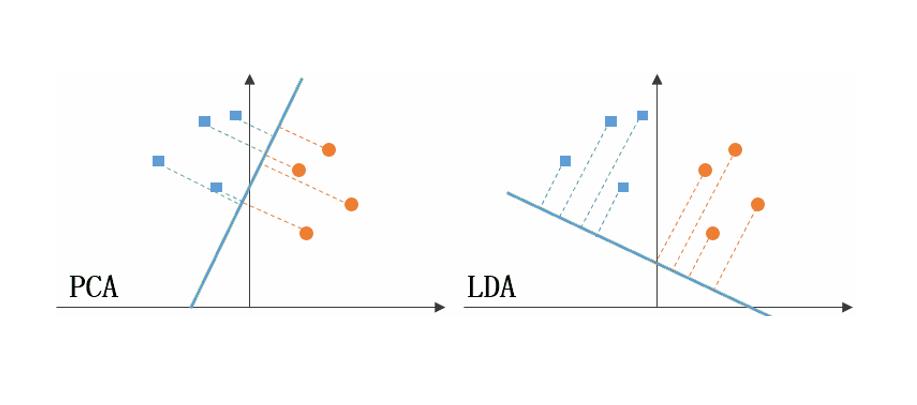
2.2 实现思路
投影后
类内方差最小,类间方差最大
就像是上面的那个三维映射例子一样,我们可以看到,方法2之所以更好,就是因为类内方差最小,类间方差最大。
数据映射到Rk(从d维降到k维),且希望该变换将属于同一类的样本映射得越近越好(即最小的类内距离),而将不同类的样本映射得越远越好 (即最大的类间距离)。同时还能尽能多地保留样本数据的判别信息。
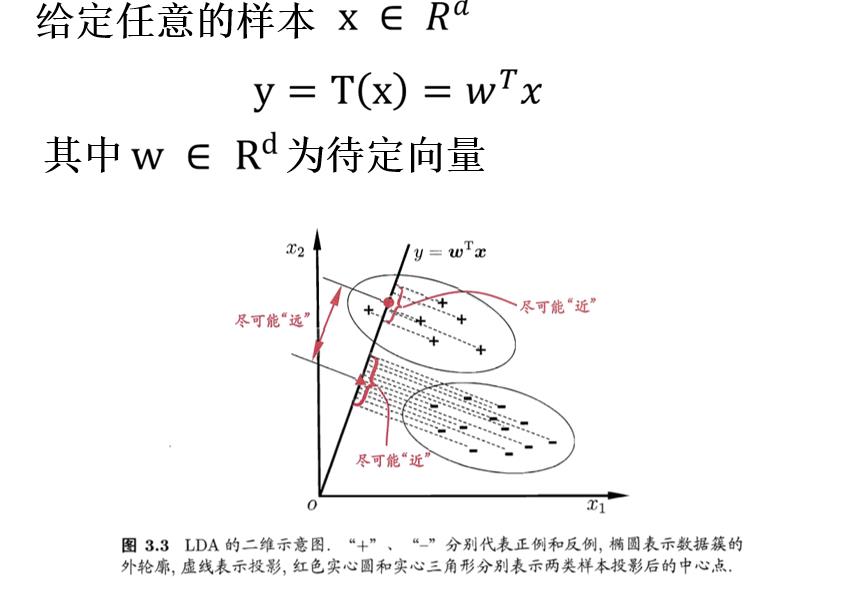
记𝒁_𝒊={𝑻(𝒙)|𝒙∊𝑿_𝒊},从而根据线性判别分析的基本思想,我们希望:
(𝒛_𝟏 ) ̅和(𝒛_2 ) ̅离的越远越好
类间离散度
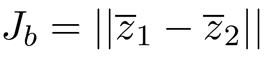
𝒁_𝒊 中的元素集中在(𝒛_𝒊 ) ̅附近越好
类内离散度


 输入:训练样本〖{𝒙_𝒊,𝒚_𝒊}〗_(𝒊=𝟏)^𝒏,降维后的维数(特征个数)k.
输入:训练样本〖{𝒙_𝒊,𝒚_𝒊}〗_(𝒊=𝟏)^𝒏,降维后的维数(特征个数)k.
输出:𝑿=[𝒙_𝟏, …,𝒙_𝒏 ]的低维度表示𝒁=[𝐳_𝟏, …,𝐳_𝒏 ].
步骤
1.计算类内散度矩阵 Sw;
2.计算类间散度矩阵 Sb;
3.计算矩阵S的负一次方wSb;
4.计算S的负一次方wSb的最大的k个特征值和对应的k个特征向量(w1, w2, …, wk),得到投影矩阵W
5.对样本集中的每一个样本特征xi转化为新的样本zi=WTxi
6.得到输出样本集〖{𝒛_𝒊,𝒚_𝒊}〗_(𝒊=𝟏)^𝒏.
2.3 小练习
给定的图像数据集,探讨LDA的降维效果
from sklearn import datasets#引入数据集
from sklearn.neighbors import KNeighborsClassifier #KNN
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt #plt用于显示图片
from matplotlib import offsetbox
def calLDA(k):
# LDA
lda = LinearDiscriminantAnalysis(n_components=k).fit(data,label) # n_components设置降维到n维度
dataLDA = lda.transform(data) # 将规则应用于训练集
return dataLDA
def calPCA(k):
# PCA
pca = PCA(n_components=k).fit(data)
# 返回测试集和训练集降维后的数据集
dataPCA = pca.transform(data)
return dataPCA
def draw():
# matplotlib画图中中文显示会有问题,需要这两行设置默认字体
fig = plt.figure('example', figsize=(11, 6))
# plt.xlabel('X')
# plt.ylabel('Y')
# plt.xlim(xmax=9, xmin=-9)
# plt.ylim(ymax=9, ymin=-9)
color = ["red","yellow","blue","green","black","purple","pink","brown","gray","Orange"]
colors = []
for target in label:
colors.append(color[target])
plt.subplot(121)
plt.title("LDA 降维可视化")
plt.scatter(dataLDA.T[0], dataLDA.T[1], s=10,c=colors)
plt.subplot(122)
plt.title("PCA 降维可视化")
plt.scatter(dataPCA.T[0], dataPCA.T[1], s=10, c=colors)
#plt.legend()
plt.show()
def plot_embedding(X,title=None):
x_min, x_max = np.min(X, 0), np.max(X, 0)
X = (X - x_min) / (x_max - x_min) # 对每一个维度进行0-1归一化,注意此时X只有两个维度
colors = ['#5dbe80', '#2d9ed8', '#a290c4', '#efab40', '#eb4e4f', '#929591','#ababab','#eeeeee','#aaaaaa','#213832']
ax = plt.subplot()
# 画出样本点
for i in range(X.shape[0]): # 每一行代表一个样本
plt.text(X[i, 0], X[i, 1], str(label[i]),
# color=plt.cm.Set1(y[i] / 10.),
color=colors[label[i]],
fontdict={'weight': 'bold', 'size': 9}) # 在样本点所在位置画出样本点的数字标签
# 在样本点上画出缩略图,并保证缩略图够稀疏不至于相互覆盖
if hasattr(offsetbox, 'AnnotationBbox'):
shown_images = np.array([[1., 1.]]) # 假设最开始出现的缩略图在(1,1)位置上
for i in range(data.shape[0]):
dist = np.sum((X[i] - shown_images) ** 2, 1) # 算出样本点与所有展示过的图片(shown_images)的距离
if np.min(dist) < 4e-3: # 若最小的距离小于4e-3,即存在有两个样本点靠的很近的情况,则通过continue跳过展示该数字图片缩略图
continue
shown_images = np.r_[shown_images, [X[i]]] # 展示缩略图的样本点通过纵向拼接加入到shown_images矩阵中
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(datasets.load_digits().images[i], cmap=plt.cm.gray_r),
X[i])
ax.add_artist(imagebox)
#plt.xticks([]), plt.yticks([]) # 不显示横纵坐标刻度
if title is not None:
plt.title(title)
plt.show()
data = datasets.load_digits().data#一个数64维,1797个数
label = datasets.load_digits().target
dataLDA = calLDA(2)
dataPCA = calPCA(2)
#draw() #普通图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plot_embedding(dataLDA,"LDA 降维可视化")
plot_embedding(dataPCA,"PCA 降维可视化")
3. 福利送书
点赞、评论即可在参与评论区的抽奖活动,抽一位小伙伴送书~
零基础也能快速入门。本书从最基础的高等数学基础讲起,由浅入深,层层递进,在巩固固有知识的同时深入讲解人工智能的算法原理,无论读者是否从事计算机相关行业,是否接触过人工智能,都能通过本书实现快速入门。全新视角介绍数学知识。采用计算机程序模拟数学推论的介绍方法,使数学知识更为清晰易懂,更容易让初学者深入理解数学定理、公式的意义,从而激发起读者的学习兴趣。理论和实践相结合。每章最后提供根据所在章的理论知识点精心设计的“综合性实例”,读者可以通过综合案例进行实践操作,为以后的算法学习奠定基础。- 大量范例
源码+习题答案,为学习排忧解难。本书所有示例都有清晰完整的源码,每章之后设有习题并配套题目答案,讲解清晰,解决读者在学习中的所有困惑。- 以后也会又很多这种
送书福利哒~,当然啦!如果没有抽到的小伙伴也可以自行前往京东或者当当购买嗷

【作者简介】
- 唐宇迪,计算机专业博士,网易云课堂人工智能认证行家,51CTO学院讲师,CSDN博客专家。
- 李琳,河南工业大学副教授,在软件工程、机器学习、人工智能和模式识别等领域有深入研究。
- 侯惠芳,教授,解放军信息工程大学通信与信息系统专业博士,擅长机器学习、大数据检索、人工智能和模式识别等。
- 王社伟,河南工业大学副教授,西北工业大学航空宇航制造专业博士,挪威科技大学访问学者,对数字化制造、企业管理系统、机器学习、数据挖掘等有丰富的实战经验。
最后
小生凡一,期待你的关注。
以上是关于☀️机器学习入门☀️ PCA 和 LDA 降维算法 | 附加小练习(文末送书)的主要内容,如果未能解决你的问题,请参考以下文章

