小Y学算法⚡️每日LeetCode打卡⚡️——33.杨辉三角

Posted 2021-10-03 呆呆敲代码的小Y

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了小Y学算法⚡️每日LeetCode打卡⚡️——33.杨辉三角相关的知识，希望对你有一定的参考价值。

📢前言

🚀 算法题 🚀

🌲 每天打卡一道算法题，既是一个学习过程，又是一个分享的过程😜
🌲 提示：本专栏解题编程语言一律使用 C# 和 Java 两种进行解题
🌲 要保持一个每天都在学习的状态，让我们一起努力成为算法大神吧🧐！
🌲 今天是力扣算法题持续打卡第33天🎈！

🚀 算法题 🚀

🌲原题样例：杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

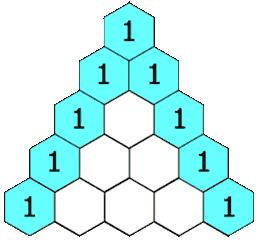
示例 1：

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2：

输入: numRows = 1
输出: [[1]]

提示：

1 <= numRows <= 30

🌻C#方法：动态规划

思路解析

使用动态规划

根据题目中给出的图形示例，我们需要定义一个 jagged(锯齿)数组，它的长度与 numRows 一样。

观察图例，不难看出，对于 i,j 这样两维访问变量，当 j=0 或 j=i 时，目标值都是 1，除此之外，目标值是 dp[i][j] = dp[i-1][j-1] + dp[i-1][j]。

代码：

public class Solution {
    public IList<IList<int>> Generate(int numRows) {
        int[][] dp =new int[numRows][];
        for(int i = 0;i<numRows;i++)
        {
            dp[i] = new int[i+1];
            for(int j = 0;j<=i;j++)
            {
                if(j==0 || j ==i)
                {
                    dp[i][j] = 1;
                }
                else
                {
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                }
            }
        }

        IList<IList<int>> p = new List<IList<int>>();
        for(int i = 1;i<= numRows;i++)
        {
            var list = dp[i-1].ToList();
            p.Add(list);
        }
        
        return p;
    }
}

执行结果

通过
执行用时：212 ms，在所有 C# 提交中击败了31.47%的用户
内存消耗：25.9 MB，在所有 C# 提交中击败了52.99%的用户

🌻Java 方法一：数学

思路解析

代码：

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> ret = new ArrayList<List<Integer>>();
        for (int i = 0; i < numRows; ++i) {
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    row.add(ret.get(i - 1).get(j - 1) + ret.get(i - 1).get(j));
                }
            }
            ret.add(row);
        }
        return ret;
    }
}

执行结果

通过
执行用时：0 ms，在所有 Java  提交中击败了100.00%的用户
内存消耗：36.3 MB，在所有 Java 提交中击败了38.54%的用户

复杂度分析

时间复杂度：O( n^2 ),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度：O( n )，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是O(logn)。

💬总结

今天是力扣算法题打卡的第三十三天！
文章采用 C#和 Java 两种编程语言进行解题
一些方法也是参考力扣大神写的，也是边学习边分享，再次感谢算法大佬们
那今天的算法题分享到此结束啦，明天再见！

🚀往期优质文章分享

以上是关于小Y学算法⚡️每日LeetCode打卡⚡️——33.杨辉三角的主要内容，如果未能解决你的问题，请参考以下文章

小Y学算法⚡️每日LeetCode打卡⚡️——8.回文数

小Y学算法⚡️每日LeetCode打卡⚡️——7.整数反转

小Y学算法⚡️每日LeetCode打卡⚡️——41. 最小栈

小Y学算法⚡️每日LeetCode打卡⚡️——10.最长公共前缀

小Y学算法⚡️每日LeetCode打卡⚡️——16.搜索插入位置

小Y学算法⚡️每日LeetCode打卡⚡️——2.两数相加