剑指offer系列——剑指 Offer 22. 链表中倒数第k个节点（C语言）

Posted 2021-10-01 未见花闻

⭐️前面的话⭐️

大家好！博主开辟了一个新的专栏——剑指offer，我要开始刷题了！这个专栏会介绍《剑指offer》书上所有的面试编程题。并且会分享一些我的刷题心得。由于博主水平有限，如有错误，欢迎指正，如果有更好的解题思路和算法可以分享给博主哦！一起加油！一起努力！

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2021年9月12日🌴
✉️坚持和努力一定能换来诗与远方！
💭参考书籍：📚《剑指offer第1版》，📚《剑指offer第2版》
💬参考在线编程网站：🌐牛客网🌐力扣
🙏作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！
博主的码云gitee，平常博主写的程序代码都在里面。

---

📌导航小助手📌

• ⭐️剑指 Offer 22. 链表中倒数第k个节点⭐️
• • 🔐题目详情
  • 💡解题思路
  • 🔑源代码
  • 🌱总结

---

⭐️剑指 Offer 22. 链表中倒数第k个节点⭐️

🔐题目详情

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。
例如，一个链表有 6 个节点，从头节点开始，它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。

示例：

给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.

限制：

无

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof

💡解题思路

方法1： 遍历。
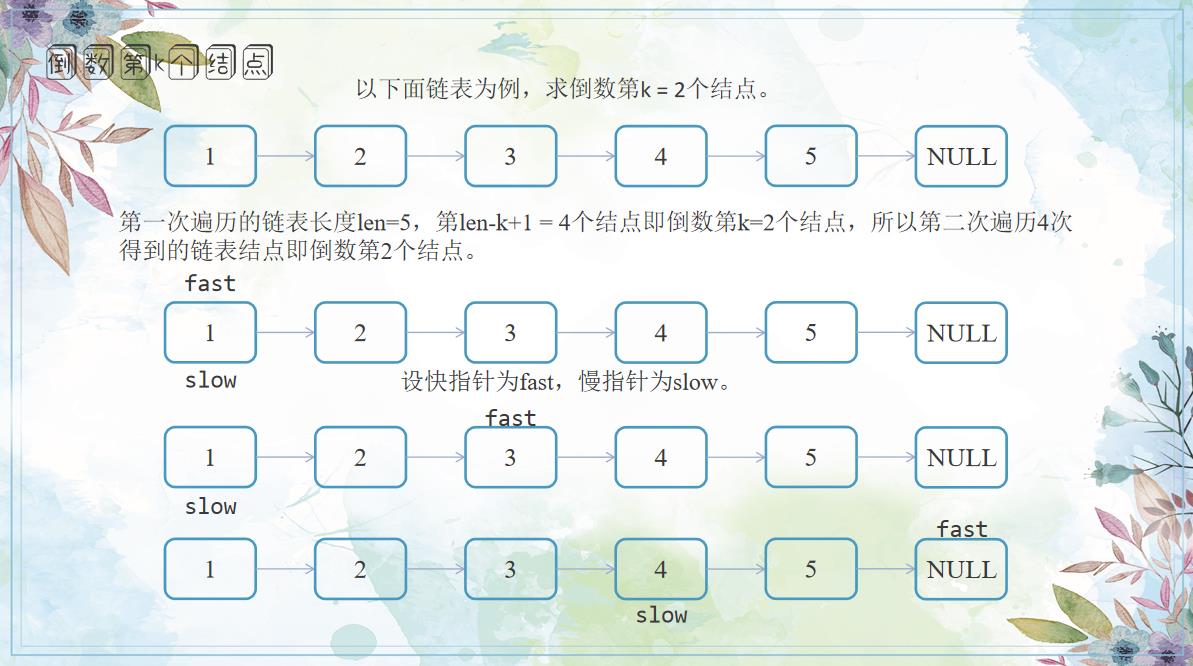
最直接的方法就是遍历链表，第一次遍历链表求出链表元素个数len，得到链表元素个数后，倒数第k个结点即第len - k + 1个结点，如果从0开始数就是第len - k个结点，所以第二次遍历目的是找到这个结点并返回这个结点的地址，遍历次数为len - k + 1。

时间复杂度： O(N)

方法2： 快慢指针。
我们都知道公交车每班车次的发出都会间隔一段时间，假设每班公交车从起点站到终点站所用时间相同，那么在这种理想情况下每相邻两班公交车到终点站的时间差即为每相邻两班发车的时间差。我们可以根据这种快慢的差异思想来思考这道题，我们需要求倒数第k个结点，我们可以让一个快指针fast先走k步，然后再让一个慢指针slow出发，fast走一步slow也走一步，等到fast走到终点时，slow刚好走到fast前面k步的位置，也就是倒数第k个结点。

时间复杂度： O(N)

🔑源代码

编程语言：C语言
在线编程平台：力扣

//方法1：
struct ListNode* getKthFromEnd(struct ListNode* head, int k){
    if(!head)
        return NULL;
    int size = 0;
    struct ListNode* cur = NULL;

    cur = head;
    while (cur)
    {
        size++;
        cur = cur->next;
    }
    int i = 0;
    cur = head;
    for (i = 0; i < size - k; i++)
    {
        cur = cur->next;
    }
    return cur;
}

//方法2：
struct ListNode* getKthFromEnd(struct ListNode* head, int k){
    if (head == NULL)
    {
        return NULL;
    }
    struct ListNode* fast = head;
    struct ListNode* slow = head;

    int i = 0;
    for(i = 0; i < k && fast; i++)
    {
        fast = fast->next;
    }
    while (fast)
    {
        slow = slow->next;
        fast = fast->next;
    }
    return slow;
}

🌱总结

求单链表倒数第k个结点，最简单直接的方法就是遍历求出链表长度然后根据链表长度找到目的结点的位置。更深一步，我们可以参考公交车发车的思想，根据遍历的结点差使用快慢指针得到倒数第k个结点。

觉得文章写得不错的老铁们，点赞评论关注走一波！谢谢啦！