遗传算法详解与MATLAB实现
Posted slandarer
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了遗传算法详解与MATLAB实现相关的知识,希望对你有一定的参考价值。
1算法讲解
1.1遗传算法流程描述
- 我们先随机生成几个个体(数值),
- 计算这几个个体是否适合当前环境(带入某个评价函数后结果大不大)
- 记录一下最好的一个个体(记录一下局部最优解)
- 依据适应度选入、淘汰一些个体(结果越好的数值有越大的概率不被扔掉,但是怕局部最优解所以还有有一定概率要被扔)
- 交叉互换的方式进行变异(转换为十进制语言来说,例如我有两个数值13和15都还可以,新的两个数值我要在11-17区间内选俩)
- 基因突变的方式进行变异(在范围内变异固然好,但是怕陷入局部最优解我还是要偶尔搞点大变异,哪怕是坏的变异)
- 进入下一轮循环,重新计算对当前环境适应程度继续前面的一系列步骤
- 好多好多带后(迭代次数大于我们的设定)后,输出记录的每一轮最优解里面最好的一个。
1.2关于为什么要用二进制码表示个体信息
可控变异:
假如我们有个二进制序列1111,转换为十进制就是15
若是我们将其变为1110,十进制变为14
若是我们将其变为1101,十进制变为13
变为1011,十进制变为11
变为0111,十进制变为7
也就是说,我们可以在大部分位置数据信息不变的情况下,各种幅度的改变我们的二进制序列代表的十进制信息。
1.3目标函数值与适应值区别
适应值=目标函数值-f(x)下限
为了方便求概率才多了个这么个操作,
举几个例子
1.假设f(x)范围是[0,3]
那么三个个体函数值为[1,2,3],那么每个个体被取到的概率很自然我们就想到设置为[1,2,3]/(1+2+3)=[1/6,1/3,1/2],数值越大取到概率越大很正常
2.假设f(x)范围为[10,10.1]
三个个体函数值为[10.01,10.05,10.03],算出其概率为[0.3327,0.3340,0.3333]非常的接近,这是因为0.几的数对比与10太小了,因而减去10非常有必要。
3.假设f(x)范围为[-1,1]
万一有个体数值为负数总不能搞个负数概率叭,所以-(-1)也是很有必要的
综上我们看出Fmin的设置也需要有一定讲究,不能使适应值出现负数,也最好能使数据具有区分度,当然如果有更加合适的映射来代替线性映射也是极好(例如机器学习就常用sigmod函数来映射)。
1.4关于如何将二进制码转化为为变量数值
假设我们有一个长度为4的二进制码,则其取值范围为0000至1111即[0,15];同时我们知道最优解范围是[2,3],我们只需要将二进制码转化为十进制,并且映射到最优解取值范围就好啦,
例如1011转换为十进制为11,从区间[0,15]映射到[2,3]即为,
(11-0)/(15-0)*(3-2)+2=2.7333,
从这个转换方式我们可以看出:
- 二进制码越长,其可取值也就越多也就能把最优解区间划分的越细,也就能使结果越精确,(当然我们可以依据我们想要的精确度大体设置二进制码长度)
- 最优解区间范围一定要有!!而且一个好的最优解区间能够让我们在取较短的二进制码时依旧可以得到较为精确的结果。
1.4关于代码改进
很多很多老版代码各种循环,这里能用向量运算就用向量运算,增加量程序的整洁度和速度
2各部分代码及使用
2.1代码使用
实例描述:
f
(
x
)
=
x
+
10
s
i
n
(
5
x
)
+
7
c
o
s
(
4
x
)
,
0
≤
x
≤
9
f(x)=x+10sin(5x)+7cos(4x),0\\leq x\\leq9
f(x)=x+10sin(5x)+7cos(4x),0≤x≤9
求
x
0
=
a
r
g
m
a
x
(
f
(
x
)
)
x_0=argmax(f(x))
x0=argmax(f(x))即使
f
(
x
)
f(x)
f(x)最大的
x
x
x值
使用代码:
[Count,Result,BestMember]=Genetic1(24,6,str2sym('x+10*sin(5*x)+7*cos(4*x)'),0,9,15,0.9,200);
参数:
- 24,二进制码长度为24
- 6,个体数目为6
- str2sym(‘x+10sin(5x)+7cos(4x)’),评价函数
- 0,x取值下限
- 9,x取值上限
- 15,f(x)下限,低于这个的我们认为这个个体完全不适合在该环境下生存
- 0.9,突变概率为了防止陷入局部最优这里数值设的其实有点大,大家用的时候设置小点就好
- 200,迭代代数
关于各个参数更详细的说明往后看
计算结果:
Count =200
Result =
7.8401,7.8048,7.8443,7.8403,7.8574,8.9649
24.8050,24.3683 ,24.8271,24.8066,11.1532,14.5649
BestMember =
7.8574
24.8553
即
x
=
7.8574
x=7.8574
x=7.8574时
f
(
x
)
f(x)
f(x)取最大值
24.8553
24.8553
24.8553
画个图看确实如此:
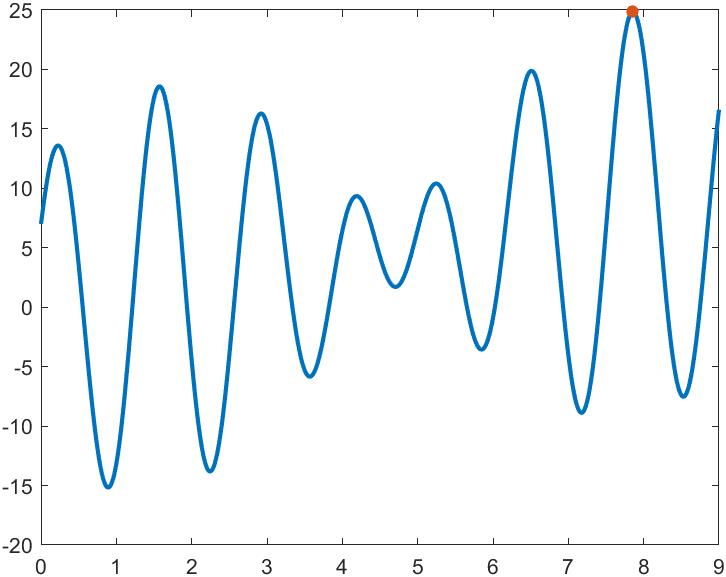
注:
遗传算法毕竟是智能算法,算出的值并不一定是最优解,因而可以调整迭代次数的大小,变异概率,二进制串长度,个体数量等一系列数据来调整,正因为各个变量比较难以说明为何这样设置,所以各种建模比赛还是尽量少用这样的智能算法。
2.2–Genetic1–主函数
function [Count,Result,BestMember]=Genetic1(MumberLength,MemberNumber,FunctionFitness,MinX,MaxX,Fmin,MutationProbability,Gen)
% 参数解释:
% 参数名 参数类型 参数含义
% =========================================================================
% MumberLength | 数值 | 表示一个染色体位串的二进制长度
% MemberNumber | 数值 | 表示群体中染色体个数
% FunctionFitness | 字符串 | 表示目标函数
% MinX | 数值 | 变量区间的下限
% MaxX | 数值 | 变量区间的上限
% Fmin | 数值 | 适应函数过程中给出目标函数可能最小值
% MutationProbability| 数值 | 变异概率
% Gen | 数值 | 遗传代数
% -------------------------------------------------------------------------
% Count | 数值 | 遗传代数
% Result | 数值 | 计算结果
% BestMember | 数值 | 最优个体及其适应值
global Count;Count=1;% 在之后的版本中可能会不支持函数输出作为全局变量(建议在改进工作中修改)
global CurrentBest; % 声明全局变量Count(代数)和CurrentBest(当前代数下的最优染色体)
% 随机地产生一个初始群体。
Population=PopulationInitialize(MumberLength,MemberNumber); PopulationCode=Population;
% 计算群体中每一个染色体的目标函数值,适应函数值,入选概率
PopulationFitness=Fitness(PopulationCode,FunctionFitness,MinX,MaxX,MumberLength);
PopulationFitnessF=FitnessF(PopulationFitness,Fmin);
PopulationProbability=Probability(PopulationFitnessF);
% 依据入选概率保留个体并记录最优个体
[Population,CurrentBest,EachGenMaxFitness]=Elitist(PopulationCode,PopulationFitness,MumberLength);
EachMaxFitness(Count)=EachGenMaxFitness;
MaxFitness(Count)=CurrentBest(MumberLength+1);
while Count<Gen
% 通过入选概率将入选概率大的个体选入种群,淘汰概率小的个体形成新群体
NewPopulation=Select(Population,PopulationProbability,MemberNumber);
Population=NewPopulation;
% 通过交叉互换形成新群体;
NewPopulation=Crossing(Population);
Population=NewPopulation;
% 通过变异形成新群体
NewPopulation=Mutation(Population,MutationProbability);
Population=NewPopulation;
% 计算新群体中每一染色体的目标函数值并借此计算出适应值与入选概率
PopulationFitness=Fitness(Population,FunctionFitness,MinX,MaxX,MumberLength);
PopulationFitnessF=FitnessF(PopulationFitness,Fmin);
PopulationProbability=Probability(PopulationFitnessF);
Count=Count+1;
% 替换当前最优个体并将最劣个体用最优个体替换
[NewPopulation,CurrentBest,EachGenMaxFitness]=Elitist(Population,PopulationFitness,MumberLength);
% EachMaxFitness,记录了第Count代中最优个体所对应的目标函数值;
% MaxFitness,前Count代中最优个体所对应的目标函数值;
EachMaxFitness(Count)=EachGenMaxFitness;
MaxFitness(Count)=CurrentBest(MumberLength+1);
Population=NewPopulation;
end
% 数据整理
Dim=size(Population);
Result=ones(2,Dim(1));
for ii=1:Dim(1)
Result(1,ii)=Translate(Population(ii,:),MinX,MaxX,MumberLength);
end
Result(2,:)=Fitness(Population,FunctionFitness,MinX,MaxX,MumberLength);
BestMember(1,1)=Translate(CurrentBest(1:MumberLength),MinX,MaxX,MumberLength);
BestMember(2,1)=CurrentBest(MumberLength+1);
% 绘图
close all
subplot(2,1,1)
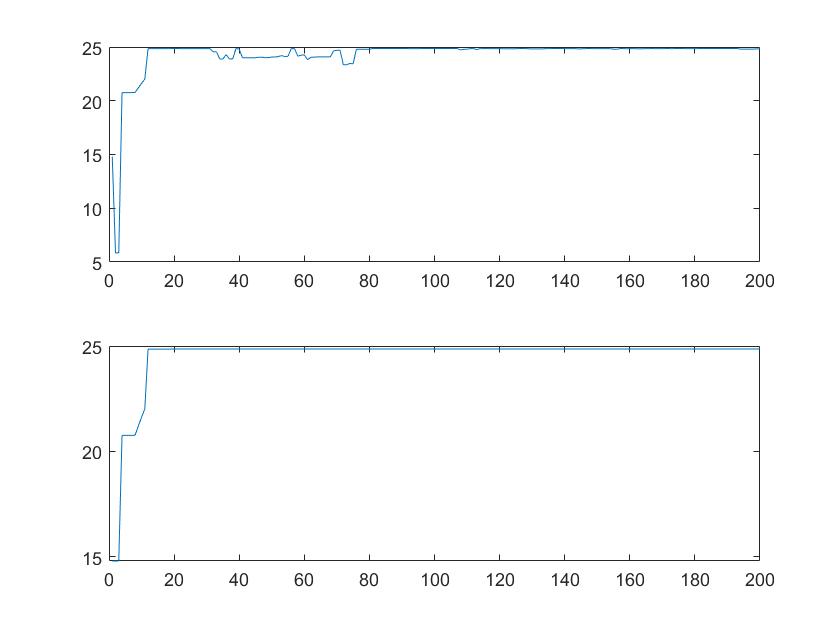
plot(EachMaxFitness);
subplot(2,1,2)
plot(MaxFitness);
end
2.3–PI(PopulationInitialize)–产生初始种群
功能: 随机地产生一个初始群体。
输入变量:
- MemberNumber代表染色体个数
- MumberLength代表每个染色体上含有MumberLength个基因(即编码长度)
输出变量: Poplation表示第一代群体
原理: 生成MemberNumber个长度为MumberLength的0-1向量
function Population=PopulationInitialize(MumberLength,MemberNumber)
Temporary=rand(MemberNumber,MumberLength);
Population=Temporary>=0.5;
% Population是一个逻辑矩阵(0-1矩阵,这么写为了方便),
% 在此函数中表示第一代群体,Population的每一行表示一个染色体
end
2.4–Fitness–计算目标函数值
功能: 计算群体中每一个染色体的目标函数值。
输入参数:
- PopulationCode表示用二进制代码表示的群体;
- FunctionFitness表示目标函数;
- MinX,MaxX分别表示变量区间的下限和上限;
- MumberLength代表一个染色体位串的二进制长度;
输出变量:
PopulationFitness表示每一染色体对应的目标函数值
原理:
这部分就是把各个二进制码转换为十进制数(区间范围内),然后再带入到目标函数中算出数值。
说明: 由于懒,这里把网上大部分代码中的Translate函数和Transfer函数也合了进去,没必要为了两行运算多开俩函数吧。。。
function PopulationFitness=Fitness(PopulationCode,FunctionFitness,MinX,MaxX,MumberLength)
Dim=size(PopulationCode);
PopulationFitness=zeros(1,Dim(1));
FunctionFitness=matlabFunction(str2sym(FunctionFitness));
for i=1:Dim(1)
% 转换为10进制
PopulationData=sum(PopulationCode(i,:).*(2.^(MumberLength-1:-1:0)));
% 映射到x取值范围
PopulationData=MinX+PopulationData*(MaxX-MinX)/(2^Dim(2)-1);
% 计算对应f(x)数值
PopulationFitness(i)=FunctionFitness(PopulationData);
end
end
2.5–FitnessF–计算适应值
功能: 计算每个染色体的适应函数值
输入参数:
PopulationFitness表示目标函数值;
Fmin表示目标函数的可能的最小值;
输出参数: PopulationFitnessF表示每一染色体的适应函数值
function PopulationFitnessF=FitnessF(PopulationFitness,Fmin)
% 若某一染色体的目标函数值大于Fmin,则置其适应函数值为其目标函数值-Fmin
% 若某一染色体的目标函数值小于Fmin,则置其适应函数值为0
PopulationFitnessF=PopulationFitness-Fmin;
PopulationFitnessF(PopulationFitnessF<0)=0;
end
2.6–Translate–将二进制码转换
这部分代码已经包含在Fitness函数内了,再写一遍是专门用来服务于最后的结果输出的。
function PopulationData=Translate(PopulationCode,MinX,MaxX,MumberLength)
Dim=size(PopulationCode);
PopulationData=sum(PopulationCode.*(2.^(MumberLength-1:-1:0)));
PopulationData=MinX+PopulationData*(MaxX-MinX)/(2^Dim(2)-1);
end
2.7–Probability–染色体入选概率
就是将适应值转换为概率,其方法就是除以所有适应值的和
function PopulationProbability=Probability(PopulationFitnessF)
PopulationProbability=PopulationFitnessF./sum(PopulationFitnessF);
end
2.8–Select–个体选择
根据入选概率在群体中按比例选择部分染色体组成种群
function NewPopulation=Select(Population,PopulationProbability,MemberNumber)
% 概率密度转换为概率分布
CProbability=PopulationProbability(1);
for i=2:MemberNumber
CProbability(i)=CProbability(i-1)+PopulationProbability(i);
end
% 摇随机数并依据随机数和概率选择个体
pmat=rand([MemberNumber,1]);
index=sum((pmat>=CProbability),2)+1;
NewPopulation=Population(index,:);
end
2.9–Crossing–交叉互换
群体中的交叉并产生新群体,原理描述如下:
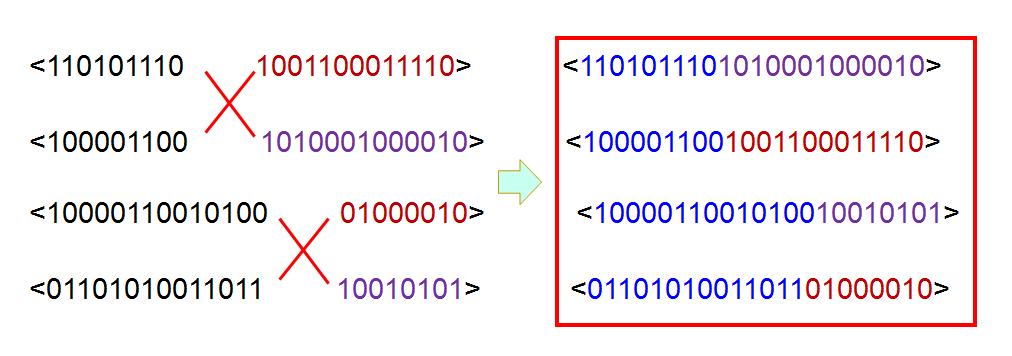
我们每次都是两个相邻的进行交叉,这样如果个体数为奇数,则最后一个个体则一直无法参与互换,因此我们每次都将倒数第一和倒数第二个体换位置,这样倒数第一位和倒数第二位就能够轮流参与交叉互换。(当然其实直接整体全部交换顺序也可以)
function NewPopulation=Crossing(Population)
Dim=size(Population);
if Dim(1)>=3
Population([Dim(1),Dim(1)-1],:)=Population([Dim(1)-1,Dim(1)],:);
% 若群体中个体数大于等于3,则将最后一个个体与倒数第二个个体基因型互换;
% 目的是防止有个体从始至终未参与交叉。
end
for i=1:2:Dim(1)-1
% 相邻的俩个体交叉互换
Site=randi(Dim(2));
Population([i,i+1],1:Site)=Population([i+1,i],1:Site);
end
NewPopulation=Population;
end
想改成全部互换则可写做:
function NewPopulation=Crossing(Population)
Dim=size(Population);
Population(1:Dim,:)=Population(randperm(Dim(1)),:);
for i=1:2:Dim(1)-1
Site=randi(Dim(2));
Population([i,i基于Matlab的遗传算法优化BP神经网络的算法实现(附算法介绍与代码详解)
基于遗传算法的BP神经网络在汇率预测中的应用研究(Matlab代码实现)