遗传算法的交叉变异详解
Posted 流浪若相惜
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了遗传算法的交叉变异详解相关的知识,希望对你有一定的参考价值。
转载:OMEGAXYZ
注:仅作学习笔记用,版权归OMEGAXYZ所有,侵权请删
文章目录
交叉
二进制编码交叉
单点交叉
单点交叉又称为简单交叉,它是指在个体编码串中只随机设置一个交叉点,然后在该点相互交换两个配体个体的部分染色体。图1为单点交叉运算的示意图。

个人理解这个应该图画错了
两点交叉
两点交叉是指在个体编码串中随机设置了两个交叉点,然后再进行部分基因交换。两点交叉的具体操作过程是:①在相互配对的两个个体编码串中随机设置两个交叉点;②交换两个个体在所设定的两个交叉点之间的部分染色体。图2为两点交叉运算示意图。
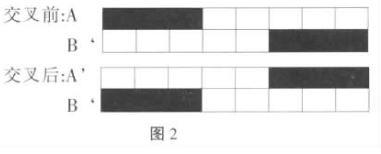
多点交叉
或称广义交叉,是指在个体编码串中随机设置多个交叉点,然后进行基因交换。其操作过程与单点交叉和两点交叉相类似。
均匀交叉
也称一致交叉,是指两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换,从而形成两个新的个体。其具体运算是通过设置一屏蔽字来确定新个体的各个基因如何由哪一个父代个体来提供。主要操作过程如下:①随机产生一个与个体编码串长度等长的屏蔽字W=w1w2Lw1Lw1,其中L为个体编码串长度;②由上述规则从A、B两个父代个体中产生出两个新的子代个体A′、B′。若ωi=0,则A′在第i个基因座上的基因值继承A的对应基因值,B′在第i个基因座上的基因值继承B的对应基因值;若ωi=1,则A′在第i个基因座上的基因值继承B的对应基因值,B′在第i个基因座上的基因值继承A的对应基因值。
均匀两点交叉
是指两个配体A、B中随机产生两个交叉点,然后按随机产生的0、1、2三个整数进行基因交换,从而形成两个新的个体[4]。当随机数是0时,配体的前面部分交叉;当随机数是1时,配体的中间部分交叉;当随机数是2时,配体的后面部分交叉。
还有其他的交叉算子,如:缩小代理交叉、洗牌交叉等。
适合浮点数编码的交叉算子
浮点数编码方法是指个体的每个基因值用某一范围内的一个浮点数来表示,个体的编码长度等于其决策变量的个数。除上述所述的适合二进制编码方法的交叉算子可用于浮点数编码方法的交叉操作中,还使用以下主要的交叉算子。
离散交叉
是指在个体之间交换变量的值,子个体的每个变量可按等概率随机地挑选父个体。
算术交叉 (NSGP算法用的中间交叉)
是指由两个个体的线性组合而产生出两个新的个体。算术交叉的操作对象一般是由浮点数编码所表示的个体.其定义为两个向量(染色体)的组合:x1=λ1×1+λ2×2;x2=λ1×2+λ2×1,其中λ1、λ2称为乘子。特殊情况有:
①当λ1=λ2=0.5时,Davis称其为平均交叉,Schwefel称其为中间交叉(intermediatecrossover);
②把乘子作为区间[-d,1+d]上的随机数时,Muh-lenbein和Schlierkamp-Voosen称其为扩展中间交叉;
启发式交叉
如果父个体1和父个体2,而父个体1有较好的适应度,则如下函数产生子个体:子个体=父个体2+Radio3(父个体1-父个体2)。其中Radio指定子代离较好适应度的父代有多远,其缺省值为1.2。
还有适合序号编码的交叉算子,如部分匹配交叉、顺序交叉、循环交叉、基于位置交换等。
变异
变异算子的基本内容是对群体中的个体串的某些基因座上的基因值作变动。依据个体编码表示方法的不同,可以有以下的算法:
a)实值变异
b)二进制变异。
一般来说,变异算子操作的基本步骤如下:
a)对群中所有个体以事先设定的变异概率判断是否进行变异
b)对进行变异的个体随机选择变异位进行变异。
遗传算法引入变异的目的有两个:一是使遗传算法具有局部的随机搜索能力。当遗传算法通过交叉算子已接近最优解邻域时,利用变异算子的这种局部随机搜索能力可以加速向最优解收敛。显然,此种情况下的变异概率应取较小值,否则接近最优解的积木块会因变异而遭到破坏。二是使遗传算法可维持群体多样性,以防止出现未成熟收敛现象。此时收敛概率应取较大值。
遗传算法中,交叉算子因其全局搜索能力而作为主要算子,变异算子因其局部搜索能力而作为辅助算子。遗传算法通过交叉和变异这对相互配合又相互竞争的操作而使其具备兼顾全局和局部的均衡搜索能力。所谓相互配合.是指当群体在进化中陷于搜索空间中某个超平面而仅靠交叉不能摆脱时,通过变异操作可有助于这种摆脱。所谓相互竞争,是指当通过交叉已形成所期望的积木块时,变异操作有可能破坏这些积木块。如何有效地配合使用交叉和变异操作,是目前遗传算法的一个重要研究内容。
基本变异算子是指对群体中的个体码串随机挑选一个或多个基因座并对这些基因座的基因值做变动(以变异概率P.做变动),(0,1)二值码串中的基本变异操作如下:
基因位下方标有*号的基因发生变异。
变异率的选取一般受种群大小、染色体长度等因素的影响,通常选取很小
遗传算法的值,一般取0.001-0.1。
参考文献
邓春燕. 遗传算法的交叉算子分析[J]. 农业网络信息, 2009(5):124-126.
前文为转载,侵权请删 原文地址:OMEGAXYZ
====================完美的分割线======================
Matlab 交叉与变异实现
交叉
变异
突变选项指定了遗传 算法如何对种群中的个体进行小的随机变化以创建突变子代。突变提供了遗传 多样性,并使遗传 算法能够搜索更广阔的空间。
‘mutationgaussian’—用于无约束问题的默认突变函数,'mutationgaussian’将从均值0的高斯分布中获取的随机数添加到父向量的每个条目。此分布的标准偏差由参数scale和 shrink以及 InitialPopulationRange选项决定。
scale参数确定第一代的标准偏差;shrink参数控制标准偏差如何随代而缩小
s
c
a
l
e
∗
(
v
(
2
)
−
v
(
1
)
)
(1)
scale*(v(2)-v(1)) \\tag1
scale∗(v(2)−v(1))(1)
δ
k
=
δ
k
−
1
∗
(
1
−
s
h
r
i
n
k
∗
k
M
a
x
G
e
n
)
(2)
δ_k=δ_k-1*(1-shrink*\\frackMaxGen) \\tag2
δk=δk−1∗(1−shrink∗MaxGenk)(2)
同时,我们可以得到,第一代的标准差
δ
1
=
s
c
a
l
e
∗
(
v
(
2
)
−
v
(
1
)
)
(3)
δ_1=scale*(v(2)-v(1)) \\tag 3
δ1=scale∗(v(2)−v(1))(3)那么,n维变量第二次迭代标准差公式可以写成
δ
2
i
=
δ
1
i
∗
(
1
−
s
h
r
i
n
k
∗
2
M
a
x
G
e
n
)
(4)
δ_2_i=δ_1_i*(1-shrink*\\frac2MaxGen) \\tag 4
δ2i=δ1i∗(1−shrink∗MaxGen2)(4)
δ
2
i
=
[
s
c
a
l
e
∗
(
v
(
2
)
−
v
(
1
)
)
]
∗
(
1
−
s
h
r
i
n
k
∗
2
M
a
x
G
e
n
)
(5)
δ_2_i=[scale*(v(2)-v(1))]*(1-shrink*\\frac2MaxGen) \\tag 5
δ2i=[scale∗(v(2)−v(1))]∗(1−shrink∗MaxGen2)(5)
依次求得k次迭代的标准差。
然后子代变量变异通过父代变量+正态随机*标准差获取,即
c
h
i
l
d
k
i
=
p
a
r
e
n
t
k
i
+
δ
k
i
∗
r
a
n
d
n
(
)
(6)
child_k_i=parent_k_i+δ_k_i*randn() \\tag 6
childki=parentki+δki∗randn()(6)
以上是关于遗传算法的交叉变异详解的主要内容,如果未能解决你的问题,请参考以下文章