[洛谷 P3376] 网络最大流 | 模板 (Dinic算法) 入门

Posted 2021-09-20 PushyTao

题目链接

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入格式

第一行包含四个正整数 $n$,$m$,$s$,$t$，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数 u_i ,v_i,w_i ，表示第 i 条有向边从 u_i 出发，到达 v_i，边权为 w_i即该边最大流量为 w_i）。
输出格式

一行，包含一个正整数，即为该网络的最大流。
输入输出样例

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

50

样例输入输出 1 解释

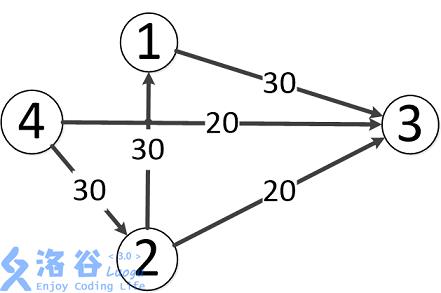
层次图：
假设在残量网络中，起点到结点u的距离为dist(u) ,我们把dist(u)看作是结点u的的层次。只保留每个点出发到下一个层次的弧，得到的图就叫做层次图，层次图上的任意路径都是“起点-> 层次1-> 层次2-> …"这样的顺序，不难发现，每条这样的路径都是s->t 的最段路
阻塞流：
阻塞流实际上就是指不考虑反向弧时的”极大流“，对应到程序里就是从起点开始在层次图中DFS，没找到一条路就进行增广
多次增广之后层次图中不存在s->t的路径，合称阻塞流
Dinic 最多会进行计算n-1 次阻塞流（每次沿阻塞流增广之后，最大距离至少会增加1），而每次阻塞流的计算时间均不超过$O(mn)$ ，实际上比这个理论界好的多

从宏观上讲，Dinic算法就是不停地用BFS来进行构造层次图，然后用阻塞流来增广。

struct Edge {
    int u, v;
    ll cap, flow;
    Edge(int _u, int _v, ll _cap, ll _flow) {
        u = _u, v = _v;
        cap = _cap, flow = _flow;
    }
};
struct Dinic {
    vector<Edge> edge;
    vector<int> G[maxn];
    ll dis[maxn],cur[maxn];
    int n,s,t;
    bool vis[maxn];
    void init(int x,int _s,int _t){
    	n = x;
    	for(int i = 0;i <= n;i++) G[i].clear();
    	s = _s,t = _t;
    	edge.clear();
    }
    void add(int u,int v,ll cap){
    	edge.push_back(Edge(u,v,cap,0));
    	edge.push_back(Edge(v,u,0,0));
    	G[u].push_back(edge.size() - 2);
    	G[v].push_back(edge.size() - 1);
    }
    bool bfs(int s,int t){
    	queue<int> que;
    	memset(vis,0,sizeof vis);
    	// memset(dis,0,sizeof dis);
    	dis[s] = 0;
    	que.push(s);
    	vis[s] = 1;
    	while(que.size()){
    		int u = que.front();
    		que.pop();
    		for(int i=0;i<G[u].size();i++){
    			int id = G[u][i];
    			int to = edge[id].v;
    			if(!vis[to] && edge[id].cap > edge[id].flow){
    				dis[to] = dis[u] + 1;
    				que.push(to);
    				vis[to] = 1;
    			}
    		}
    	}
    	return vis[t];
    }
    ll dfs(int s,int t,ll rest){
    	if(s == t || rest == 0) return rest;
    	ll sum = 0LL;
    	ll Flow = 0, f;
    	for(ll& i = cur[s];i < G[s].size();i ++){
    		Edge& e = edge[G[s][i]];
    		if(dis[s] + 1 == dis[e.v] && (f = dfs(e.v ,t,min(rest,e.cap - e.flow))) > 0){
    			e.flow += f;
    			edge[G[s][i] ^ 1].flow -= f;
    			Flow += f;
    			rest -= f;
    			if(rest == 0) break;
    		}
    	}
    	return Flow;
    }
    ll getMaxFlow(int s,int t){
    	ll ans = 0;
    	while(bfs(s,t)) {
    		memset(cur,0,sizeof cur);
    		ans += dfs(s,t,0x3f3f3f3f);
    	}
    	return ans;
    }
} solve;
int main() {
    int n = read,m = read,s = read,t = read;
    solve.init(n,s,t);
    for(int i=1;i<=m;i++){
    	ll u = read,v = read,cap = read;
    	solve.add(u,v,cap);
    }
    cout << solve.getMaxFlow(s,t) <<endl;
    return 0;
}