C++从入门到入土第二十二篇：数据结构之红黑树

Posted 2021-09-20 李憨憨_

红黑树

---

文章目录

• 红黑树
• 一、红黑树
• • 简介
  • 性质
  • 节点
  • 红黑树的实现

---

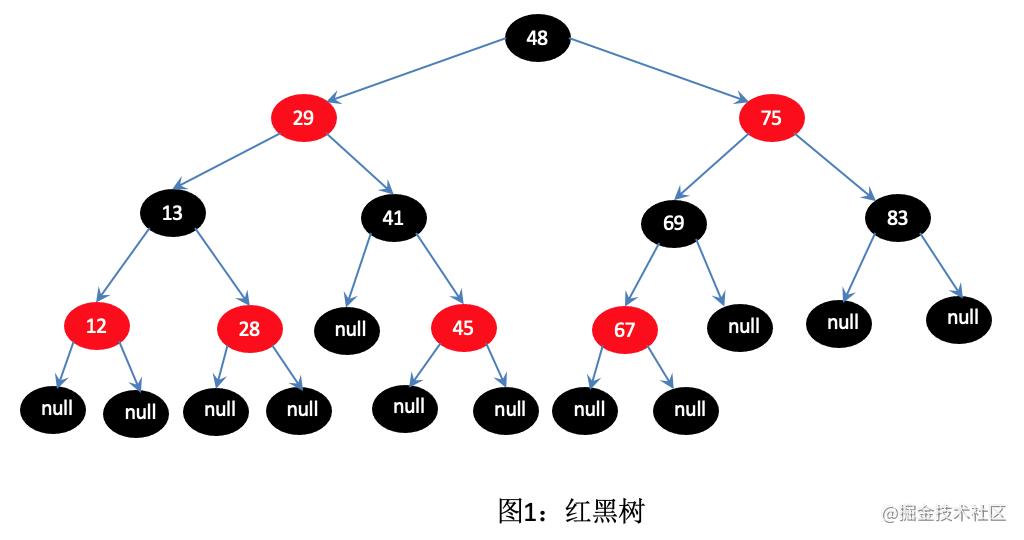
一、红黑树

红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。
它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

简介

红黑树是一种特定类型的二叉树，它是在计算机科学中用来组织数据比如数字的块的一种结构。
红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但 对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。
由于每一棵红黑树都是一颗二叉排序树，因此，在对红黑树进行查找时，可以采用运用于普通二叉排序树上的查找算法，在查找过程中不需要颜色信息。

性质

红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:
 性质1. 结点是红色或黑色。
 性质2. 根结点是黑色。
 性质3. 所有叶子都是黑色。（叶子是NIL结点）
 性质4. 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
 性质5. 从任一节结点其每个叶子的所有路径都包含相同数目的黑色结点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。
是性质4导致路径上不能有两个连续的红色结点确保了这个结果。最短的可能路径都是黑色结点，最长的可能路径有交替的红色和黑色结点。因为根据性质5所有最长的路径都有相同数目的黑色结点，这就表明了没有路径能多于任何其他路径的两倍长。
因为红黑树是一种特化的二叉查找树，所以红黑树上的只读操作与普通二叉查找树相同。

节点

template <class K, class V>
struct RBNode
{
	//typedef bool color;

	RBNode<K, V>* _parent;
	RBNode<K, V>* _left;
	RBNode<K, V>* _right;

	pair<K, V> _kv;
	//颜色
	COLOR _color;

	RBNode(const pair<K, V>& kv = pair<K, V>())
		:_parent(nullptr)
		, _left(nullptr)
		, _right(nullptr)
		, _kv(kv)
		, _color(RED)
	{}
};

红黑树的实现

template <class K, class V>
class RBTree
{
public:
	typedef RBNode<K, V> Node;

	RBTree()
		:_header(new Node)
	{
		//创建空树
		_header->_left = _header->_right = _header;
	}

	bool insert(const pair<K, V>& kv)
	{
		//1. 搜索树的插入
		//空树: _header->parent: nullptr
		if (_header->_parent == nullptr)
		{
			//创建根节点
			Node* root = new Node(kv);

			_header->_parent = root;
			root->_parent = _header;
			_header->_left = _header->_right = root;

			//根节点是黑色
			root->_color = BLACK;
			return true;
		}

		//从根节点开始搜索
		Node* cur = _header->_parent;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;
			//和key值进行比较
			if (cur->_kv.first == kv.first)
			{
				//key值不允许重复
				return false;
			}
			else if (cur->_kv.first > kv.first)
			{
				cur = cur->_left;
			}
			else
			{
				cur = cur->_right;
			}
		}

		//创建待插入的节点
		cur = new Node(kv);
		if (parent->_kv.first > cur->_kv.first)
			parent->_left = cur;
		else
			parent->_right = cur;
		cur->_parent = parent;

		//2. 修改颜色或调整结构
		//判断是否有红色连续的节点
		while (cur != _header->_parent && cur->_parent->_color == RED)
		{
			parent = cur->_parent;
			Node* gfather = parent->_parent;

			if (gfather->_left == parent)
			{
				Node* uncle = gfather->_right;
				//1.uncle是存在的，并且是红色的
				if (uncle && uncle->_color == RED)
				{
					parent->_color = uncle->_color = BLACK;
					gfather->_color = RED;
					//继续更新
					cur = gfather;
				}
				else
				{
					//cout << "Rotate" << endl;
					//判断是否为双旋的场景
					if (cur == parent->_right)
					{
						//左旋
						RotateL(parent);
						//交换cur, parent指向，退化成右旋的场景
						swap(cur, parent);
					}
					//右旋
					RotateR(gfather);
					parent->_color = BLACK;
					gfather->_color = RED;
					break;
				}
			}
			else
			{
				Node* uncle = gfather->_left;
				if (uncle && uncle->_color == RED)
				{
					parent->_color = uncle->_color = BLACK;
					gfather->_color = RED;
					cur = gfather;
				}
				else
				{
					//cout << "Rotate" << endl;
					if (cur == parent->_left)
					{
						RotateR(parent);
						swap(cur, parent);
					}
					RotateL(gfather);
					parent->_color = BLACK;
					gfather->_color = RED;
					break;
				}
			}
		}
		//根节点的颜色改成黑色
		_header->_parent->_color = BLACK;
		//更新header的左右指向
		_header->_left = leftMost();
		_header->_right = rightMost();
		return true;
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		subR->_left = parent;
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		//判断根
		if (parent == _header->_parent)
		{
			_header->_parent = subR;
			subR->_parent = _header;
		}
		else
		{
			Node* pparent = parent->_parent;
			if (pparent->_left == parent)
				pparent->_left = subR;
			else
				pparent->_right = subR;
			subR->_parent = pparent;
		}
		parent->_parent = subR;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		subL->_right = parent;
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		//判断根
		if (parent == _header->_parent)
		{
			_header->_parent = subL;
			subL->_parent = _header;
		}
		else
		{
			Node* pparent = parent->_parent;
			if (pparent->_left == parent)
				pparent->_left = subL;
			else
				pparent->_right = subL;
			subL->_parent = pparent;
		}
		parent->_parent = subL;
	}

	Node* leftMost()
	{
		Node* cur = _header->_parent;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return cur;
	}

	Node* rightMost()
	{
		Node* cur = _header->_parent;
		while (cur && cur->_right)
		{
			cur = cur->_right;
		}
		return cur;
	}

	void inorder()
	{
		_inorder(_header->_parent);
		cout << endl;
	}

	void _inorder(Node* root)
	{
		if (root)
		{
			_inorder(root->_left);
			cout << root->_kv.first << " ";
			_inorder(root->_right);
		}
	}

	//红黑树
	//1. 根： 黑色
	//2. 每条路径黑色个数相同
	//3. 红色不能连续
	bool isbalance()
	{
		if (_header->_parent == nullptr)
			return true;
		Node* root = _header->_parent;
		if (root->_color == RED)
			return false;
		//统计一条路径上的黑色节点个数
		int bCount = 0;
		Node* cur = root;
		while (cur)
		{
			if (cur->_color == BLACK)
				++bCount;
			cur = cur->_left;
		}
		//遍历每一条路径
		int curBCount = 0;
		return _isblance(root, bCount, curBCount);
	}

	bool _isblance(Node* root, int& bCount, int curBCount)
	{
		//当root为空时，一条路径遍历结束
		if (root == nullptr)
		{
			//判断黑色节点个数是否相同
			if (curBCount != bCount)
				return false;
			else
				return true;
		}
		//判断节点是否为黑色
		if (root->_color == BLACK)
			++curBCount;

		//判断是否有红色连续节点
		if (root->_parent && root->_color == RED && root->_parent->_color == RED)
		{
			cout << "data: " << root->_kv.first << endl;
			return false;
		}
		return _isblance(root->_left, bCount, curBCount) 
		&& _isblance(root->_right, bCount, curBCount);
	}

	//成员： header
private:
	Node* _header;
};