Add or Multiply 1 (第二类Strling 数)

Posted 2021-09-20 goto_1600

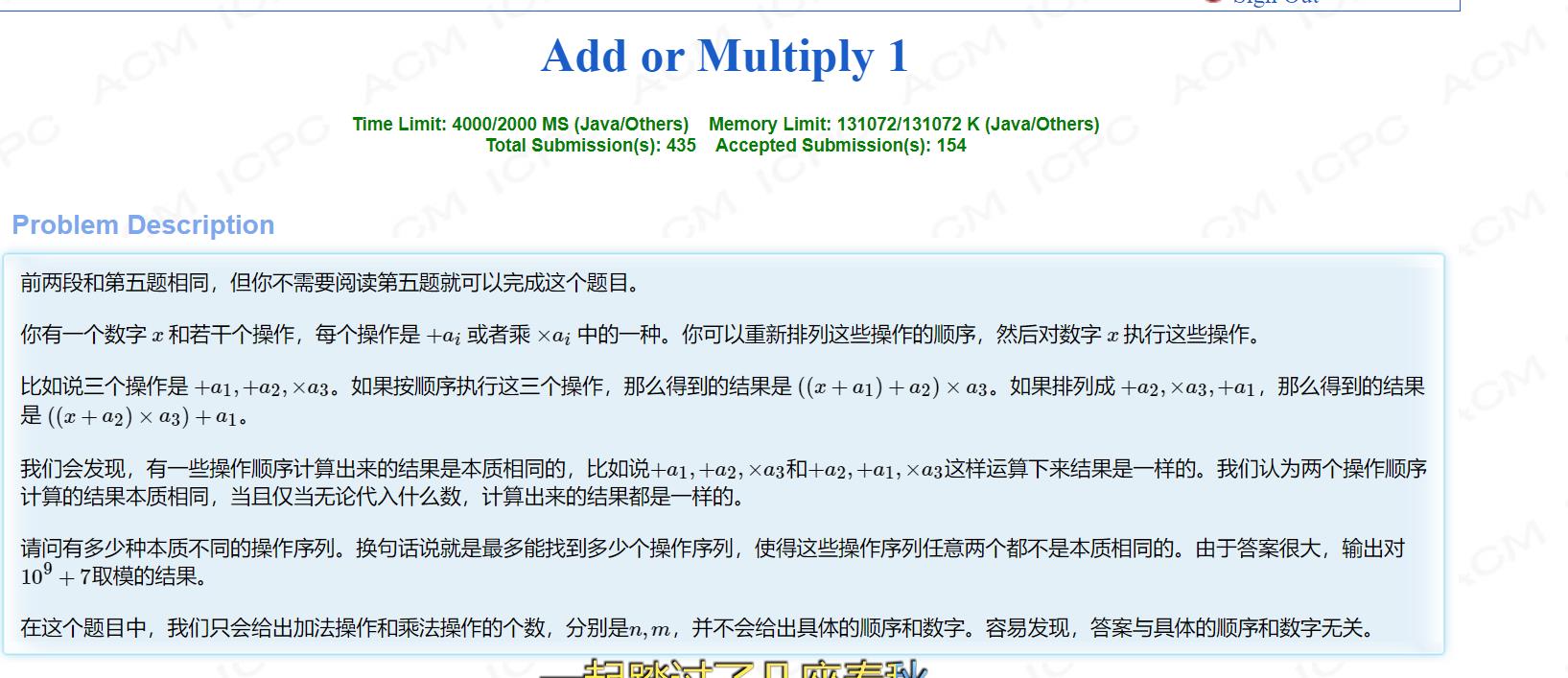
题意：
给定n个加数m个乘数求最后本质不同的多项式数量。
思路：
有一个性质，假设先单独讨论加法，对于某个数ai，我们假设加法和乘法组数为x和y，对于不同组之间的ai，无法构造出和刚才序列相同的多项式。那么启发我们思考，对于加法和乘法两个是独立的，加法组内无序，乘法组内也是无序，但单单对组数有要求，|x-y|<=1才可以，例如$$++--++，--++--，--++,++--$$x和y是加法乘法的组数。而且组和组之间也是有序的，f[i][j]代表i个数分为j组的方案数，由于第二类斯特林数求的是无序，那么我们预处理的时候要注意一下。然后计算就可以了。当x=y的时候注意要乘以2，因为加法放在前面和乘法放在前面是不一样的。
代码：

#include <bits/stdc++.h>
#define IL inline
#define x first
#define y second
typedef long long ll;
using namespace std;
const int mod= 1e9 + 7;
const int N= 3010;
ll f[N][N];
int fact[N];
int qmi(int a, int b)
{
    int res= 1;
    while (b) {
        if (b & 1)
            res= 1ll * res * a % mod;
        b>>= 1;
        a= 1ll * a * a % mod;
    }
    return res;
}
int main()
{
    f[0][0]= 1;
    fact[0]= 1;
    for (int i= 1; i < N; i++)
        fact[i]= 1ll * fact[i - 1] * i % mod;
    for (int i= 1; i < N; i++) {
        for (int j= 1; j <= i; j++)
            f[i][j]= (f[i - 1][j - 1] + j * 1ll * f[i - 1][j]) % mod;
    }
    for (int i= 1; i < N; i++)
        for (int j= 1; j <= i; j++)
            f[i][j]= f[i][j] * fact[j] % mod;
    int t;
    cin >> t;
    while (t--) {
        int n, m;
        cin >> n >> m;
        ll res= 0;
        for (int i= 1; i <= min(n, m); i++) {
            res= (res + 2 * f[n][i] * f[m][i] % mod) % mod;
        }
        for (int i= 1; i <= max(n, m); i++) {
            res= (res + f[n][i] * f[m][i + 1]) % mod;
            res= (res + f[n][i] * f[m][i - 1]) % mod;
        }

        cout << res << endl;
    }
    return 0;
}