hdu7095 Add or Multiply 1（思维，组合数学，第二类斯特林数预处理）

Posted 2021-09-10 live4m

题意：

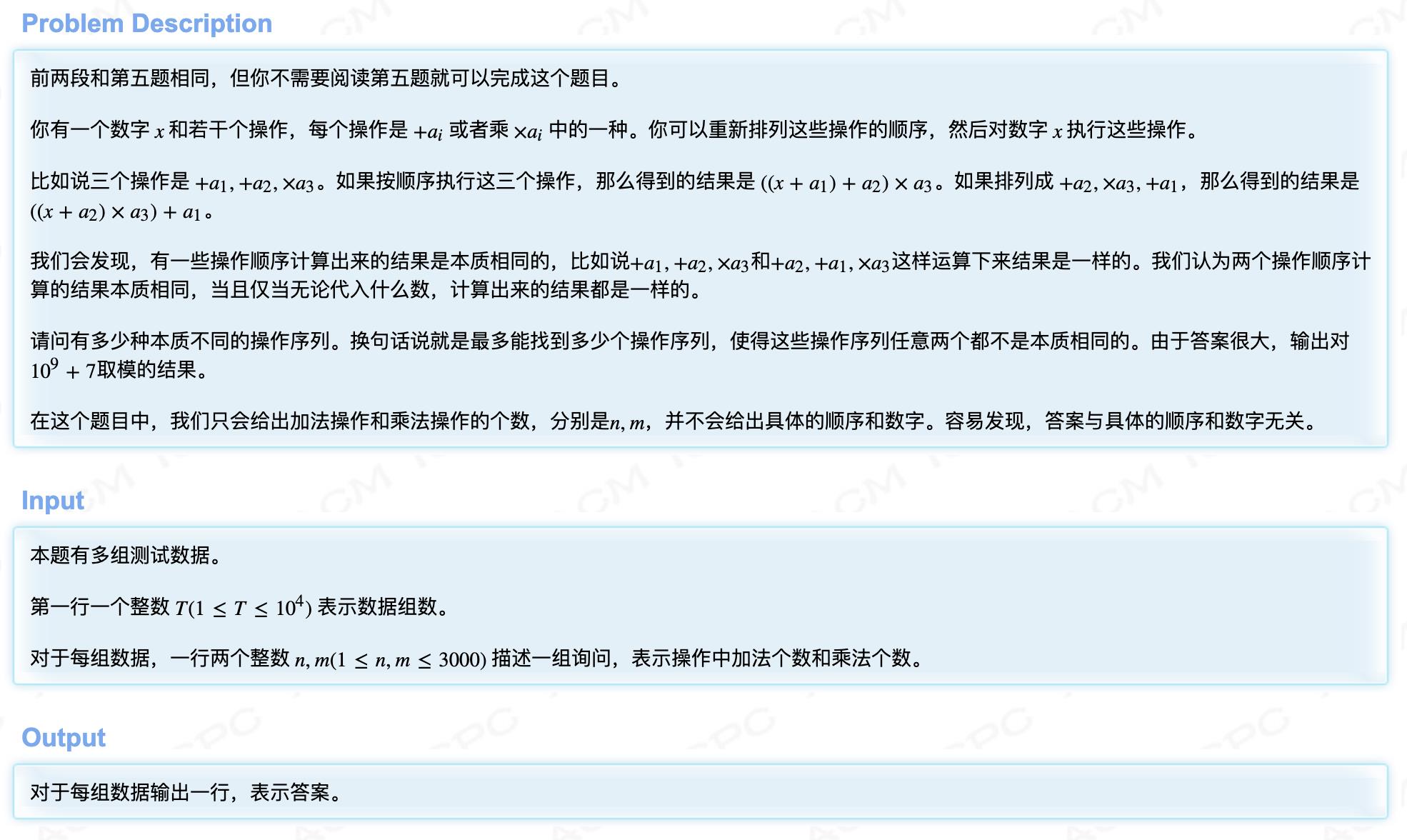
解法：

题目提示了答案与具体的顺序和数字无关,
容易发现对于连续的+++和连续的***,内部的数字更换顺序对结果没有影响,即等价.

那么只需要考虑有几堆*,和几堆+即可.

直接算不好算,考虑O(m)枚举*的堆数,利用组合数学O(1)计算方案数字,
假设当前有i堆*,那么有中间i-1个空隙,左边空隙,右边空隙.
为了有i堆,显然中间i-1个空隙至少有一个+,
那么n个+有三种摆放情况:
中间和左右都用上了,即分成i+1堆,
中间和左边用上了,或者中间和右边用上了,即分成了i堆,
只有中间用上了,分成了i-1堆.

n个+分成x堆,这是球不同盒不同的方案数,
答案为d[n][x],d是第二类斯特林数.
由于x堆可以互换顺序,因此方案数还需要乘上x的阶乘

同理,m个*分成i堆,方案数为d[m][i],
由于m堆可以打乱顺序,因此方案数还需要乘上i的阶乘.

对每部分计算方案数,累加就是答案了.

ps:
第二类斯特林数需要O(n^2)预处理.

code：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxm=3333;
const int mod=1e9+7;
int d[3333][3333];
int fac[maxm];
int n,m;
void solve(){
    cin>>n>>m;
    int ans=0;
    //枚举乘法的堆数
    for(int i=1;i<=m;i++){
        int cnt1=d[m][i]*fac[i]%mod;
        //两边都有,i+1堆
        int cnt2=d[n][i+1]%mod;
        ans=(ans+cnt1*cnt2%mod*fac[i+1]%mod)%mod;
        //只有一边有*2,i堆
        cnt2=d[n][i]%mod;
        ans=(ans+cnt1*cnt2*2%mod*fac[i]%mod)%mod;
        //两边都没有,i-1堆
        cnt2=d[n][i-1]%mod;
        ans=(ans+cnt1*cnt2%mod*fac[i-1]%mod)%mod;
    }
    cout<<ans<<endl;
}
void init(){
	fac[0]=1;
    for(int i=1;i<maxm;i++)fac[i]=fac[i-1]*i%mod;
    //i个数分为j组
    d[1][1]=1;
    for(int i=2;i<maxm;i++){
        d[i][1]=1;
        for(int j=2;j<maxm;j++){
            d[i][j]=(d[i-1][j-1]+d[i-1][j]*j%mod)%mod;
        }
    }
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);
    init();
    int T;cin>>T;while(T--)
    solve();
    return 0;
}

---