动态规划_计数类dp_数位统计dp_状态压缩dp_树形dp_记忆化搜索
Posted 一只特立独行的猫
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划_计数类dp_数位统计dp_状态压缩dp_树形dp_记忆化搜索相关的知识,希望对你有一定的参考价值。
目录
计数类dp
给定方案限制,统计某一种方案出现个数
原题链接
https://www.acwing.com/problem/content/902/
题目大意
一个正整数 n 可以表示成若干个正整数之和,形如:n=n1+n2+…+nk,中 n1≥n2≥…≥nk,k≥1。
我们将这样的一种表示称为正整数 n的一种划分。现在给定一个正整数 n
,请你求出 n 共有多少种不同的划分方法。
0<n<=1000
思路
通过完全背包解决。
f
(
i
,
j
)
f(i,j)
f(i,j)表示前
i
i
i个数放入容量为
j
j
j的背包的组合数量。由于使用
[
1
−
(
j
−
1
)
]
[1-(j-1)]
[1−(j−1)]凑
j
j
j,所以一定可以凑满。
朴素版:
状态表示:
f
(
i
,
j
)
f(i,j)
f(i,j)表示用1到i的数凑j的数量
状态计算:
f
(
i
,
j
)
=
f
(
i
−
1
,
j
)
+
f
(
i
−
1
,
j
−
1
∗
i
)
+
f
(
i
−
1
,
j
−
2
∗
i
)
+
.
.
.
f(i,j)=f(i-1,j)+f(i-1,j-1*i)+f(i-1,j-2*i)+...
f(i,j)=f(i−1,j)+f(i−1,j−1∗i)+f(i−1,j−2∗i)+...
优化版:
状态表示:同朴素版,但是用到了滚动数组优化
状态计算:
f
(
j
)
=
f
(
j
)
+
f
(
j
−
i
)
f(j)=f(j)+f(j-i)
f(j)=f(j)+f(j−i)
具体的证明看这篇博客。
https://blog.csdn.net/qq_45931661/article/details/119999547
其他版
状态表示:
f
(
i
,
j
)
f(i,j)
f(i,j)表示用
j
j
j个数凑
i
i
i的数量
状态计:
f
(
i
,
j
)
=
f
(
i
−
1
,
j
−
1
)
+
f
(
i
−
j
,
j
)
f(i,j)=f(i-1,j-1)+f(i-j,j)
f(i,j)=f(i−1,j−1)+f(i−j,j)
代码
朴素版,O(n^3)的复杂度
#include<iostream>
using namespace std;
const int N = 1005,mod = 1e9+7;
int n;
int f[N][N];
int main(){
cin>>n;
for(int i=0;i<=n;i++) f[i][0]=1;
for(int i=1;i<=n;i++){//枚举物品
for(int j=1;j<=n;j++){//枚举背包容量
for(int k=0;k*i<=j;k++){//状态计算
f[i][j]=(f[i][j]+f[i-1][j-k*i])%mod;
}
}
}
cout<<f[n][n]<<endl;
return 0;
}
优化版,O(n^2)的复杂度。
#include<iostream>
using namespace std;
const int N = 1005,mod = 1e9+7;
int n;
int f[N];
int main(){
cin>>n;
f[0]=1;
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){//滚动状态计算
f[j]=(f[j]+f[j-i])%mod;
}
}
cout<<f[n]<<endl;
return 0;
}
其他版:
#include<iostream>
using namespace std;
const int N = 1005,mod = 1e9+7;
int n;
int f[N][N];
int main(){
cin>>n;
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){//状态计算
f[i][j]=(f[i-1][j-1]+f[i-j][j])%mod;
}
}
int res = 0 ;
for(int i=1;i<=n;i++){//求总共的数量
res=(res+f[n][i])%mod;
}
cout<<res<<endl;
return 0;
}
数位统计DP
统计数字中的一些规律,如出现数字的次数等等。
题目链接:
https://www.acwing.com/problem/content/340/
题目大意:
给定两个整数 a 和 b,求 a 和 b 之间的所有数字中 0∼9的出现次数。
例如,a=1024,b=1032,则 a 和 b 之间共有 9个数如下:
1024 1025 1026 1027 1028 1029 1030 1031 1032
其中 0 出现 10次,1 出现 10 次,2 出现 7 次,3 出现 3 次等等…
思路:
求[a,b]区间内x出现的次数,可以采用前缀和的思想,
r
e
s
=
c
o
u
n
t
(
b
,
x
)
−
c
o
u
n
t
(
a
−
1
,
x
)
res=count(b,x)-count(a-1,x)
res=count(b,x)−count(a−1,x)
现在分析如何求解
c
o
u
n
t
(
a
,
x
)
count(a,x)
count(a,x),即[1,a]中x出现的次数。
设要求的数为abcdefg
以分析第4位出现x的情况为例:
- x!=0
1.形式: { 0 − ( a b c − 1 ) } d { 0 − 1000 } \\{0 - (abc-1)\\}d\\{0-1000\\} {0−(abc−1)}d{0−1000}
意义:前缀小于abc的情况
2.1.形式: a b c d { 0 − 1000 } abcd\\{0-1000\\} abcd{0−1000}
意义:d==x的情况
2.2 形式: a b c d { 0 − e f g } abcd\\{0-efg\\} abcd{0−efg}
意义:d<x的情况
2.3 形式:不存在
意义:d>x的情况 - x==0
1.形式: { 1 − ( a b c − 1 ) } d { 0 − 1000 } \\{1 - (abc-1)\\}d\\{0-1000\\} {1−(abc−1)}d{0−1000}
意义:前缀小于abc的情况,但是要注意0的前缀不能为0,否则就没有意义了。
2.1.形式: a b c d { 0 − 1000 } abcd\\{0-1000\\} abcd{0−1000}
意义:d==x的情况
2.2 形式: a b c d { 0 − e f g } abcd\\{0-efg\\} abcd{0−efg}
意义:d<x的情况
2.3 形式:不存在
意义:d>x的情况
枚举每一位上的x出现的次数,就可以的到最终的答案。
代码:
#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
int n,m;
int get(vector<int > num, int r, int l){
//将num的r到l位化成一个数字
int res=0;
for(int i=r;i>=l;i--){
res=res*10+num[i];
}
return res;
}
int count(int a,int x){
//统计1~a当中x出现的次数
if(a==0) return 0;
vector<int > num;//存储每一位
while(a){
//低下标放低位
num.push_back(a%10);
a/=10;
}
int n = num.size();
long long res=0;
for(int i=n-1-!x;i>=0;i--){
//从高到低枚举每一位
res+=(long long )get(num,n-1,i+1)*pow(10,i);//1情况
if(!x) res-=pow(10,i);
if(x==num[i]) res+=get(num,i-1,0)+1;//2.1情况
else if(x<num[i]) res+=pow(10,i);//2.2情况
}
return res;
}
int main(){
while(cin>>n>>m,n||m){
if(n>m) swap(n,m);
for(int i=0;i<10;i++){
cout<<count(m,i)-count(n-1,i)<<" ";//利用前缀和的思想
}
cout<<endl;
}
return 0;
}
状态压缩DP
通过将状态用二进制位表示来实现dp的过程。
蒙德里安的梦想
原题链接:
https://www.acwing.com/problem/content/293/
题目大意:
求把 N×M 的棋盘分割成若干个 1×2的的长方形,有多少种方案。
例如当 N=2,M=4时,共有 5 种方案。当 N=2,M=3 时,共有 3种方案。
如下图所示:

思路:
1.可以发现,一旦给定横着的积木的位置,竖着的积木的位置也确定了。
2.用j的二进制来表示每一列的状态。如下图,第i列的状态就是
(
100
)
2
(100)_2
(100)2
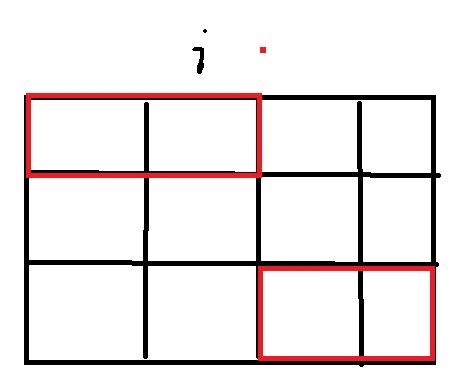
**状态表示:
f
(
i
,
j
)
f(i,j)
f(i,j)表示第
i
i
i列, 状态为
j
j
j的填充方案个数。

状态计算: f ( i , j ) + = f ( i − 1 , k ) f(i,j)+=f(i-1,k) f(i,j)+=