机器学习入门 KNN分类算法 | 附加小练习
Posted 小生凡一
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习入门 KNN分类算法 | 附加小练习相关的知识,希望对你有一定的参考价值。
1. 聚类与分类
1.1 聚类
聚类是将数据对象的集合分成相似的对象类的过程。使得同一个簇(或类)中的对象之间具有较高的相似性,而不同簇中的对象具有较高的相异性,并且事先不知道数据集本身有多少类别,属于无监督学习。
e.g:
比如预测某一学校的在校大学生的好朋友团体,我们不知道大学生和谁关系好或和谁关系不好,我们通过他们的相似度进行聚类,聚成n个团体,这就是聚类。
1.2 分类
分类就是事先已知道数据集中包含多少种类,从而对数据集中每一样本进行分类,且所分配的标签必须包含在已知的标签集中,属于监督学习。
e.g:
比如对一个学校的在校大学生进行性别分类,我们会下意识很清楚知道分为“男”,“女”。对于一个分类器,通常需要你告诉它“这个东西被分为某某类”。
2. 关于KNN算法
邻近算法,或者说K最近邻分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是K个最近的邻居的意思,说的是每个样本都可以用它最接近的K个邻居来代表,KNN是通过测量不同特征值之间的距离进行分类。(后续有例题)
2.1 Lp距离定义:
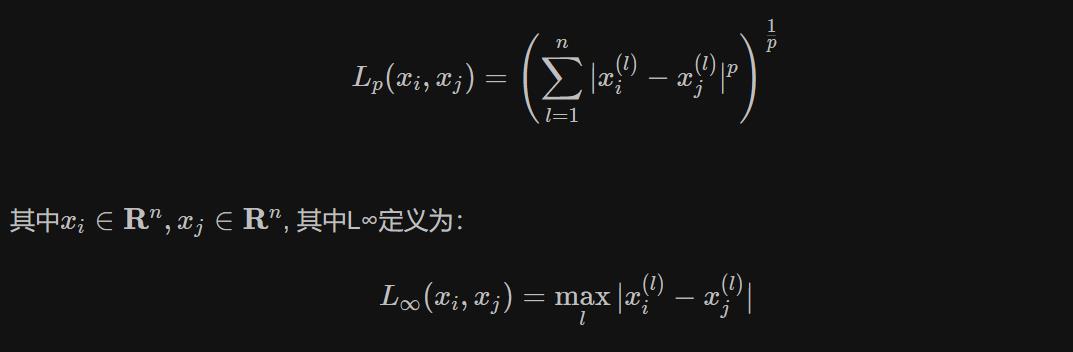
-
当p=1时,就是曼哈顿距离(对应L1范数)
-
当p=2时,就是欧氏距离(对应L2范数)
2.1 K值的选取
-
如果选择较小的
K值,就相当于用较小的邻域中的训练实例进行预测,学习的近似误差会减小,只有与输入实例较近的训练实例才会对预测结果起作用,但缺点是学习的估计误差会增大,预测结果会对近邻的实例点分成敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,K值减小就意味着整体模型变复杂,分的不清楚,就容易发生过拟合。 -
如果选择较大
K值,就相当于用较大邻域中的训练实例进行预测,其优点是可以减少学习的估计误差,但近似误差会增大,也就是对输入实例预测不准确,K值得增大就意味着整体模型变的简单。
3. 练习
使用Sklearn中的make_circles方法生成训练样本,随机生成测试样本,用KNN分类并可视化。
第一题:
"""
Sklearn中的make_circles方法生成训练样本
并随机生成测试样本,用KNN分类并可视化。
"""
from sklearn.datasets import make_circles
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import numpy as np
import random
fig = plt.figure(1, figsize=(10, 5))
x1, y1 = make_circles(n_samples=400, factor=0.4, noise=0.1)
# 模型训练 求距离、取最小K个、求类别频率
knn = KNeighborsClassifier(n_neighbors=15)
knn.fit(x1, y1) # X是训练集(横纵坐标) y是标签类别
# SVM 支持向量机(Support Vector Machine)
"""
置信风险与两个量有关,一是样本数量,显然给定的样本数量越大,我们的学习结果越有可能正确,
此时置信风险越小;二是分类函数的VC维,显然VC维越大,推广能力越差,置信风险会变大。
公式中R(w)就是真实风险,Remp(w)就是经验风险,Ф(n/h)就是置信风险。
统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小,即结构风险最小。
SVM正是这样一种努力最小化结构风险的算法.
SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能大的间隙。
# 进行预测
x2 = random.random() # 测试样本横坐标
y2 = random.random() # 测试样本纵坐标
X_sample = np.array([[x2, y2]]) # 给测试点
# y_sample = knn.predict(X_sample) # 调用knn进行predict得预测类别
y_sample = []
for i in range(0, 400):
dx = x1[:, 0][i] - x2
dy = x1[:, 1][i] - y2
d = (dx ** 2 + dy ** 2) ** 1 / 2
y_sample.append(d)
neighbors = knn.kneighbors(X_sample, return_distance=False)
plt.subplot(121)
plt.title('data by make_circles() 1')
plt.scatter(x1[:, 0], x1[:, 1], marker='o', s=100, c=y1)
# 这个s就是点的大小 marker是标记的意思,就是说用什么标记,比如这里用o来标记,可以尝试换成其他可行的marker试试。
# 这个x1[:,0] 就是选取x1的全部元素里面的第0列
# 这个x1[:,1] 就是选取x1的全部元素里面的第1列
# c就是颜色的意思,就是按照y1的分类进行填充颜色
plt.scatter(x2, y2, marker='*', c='b')
plt.subplot(122)
plt.title('data by make_circles() 2')
plt.scatter(x1[:, 0], x1[:, 1], marker='o', s=100, c=y1)
plt.scatter(x2, y2, marker='*', c='r', s=100)
for i in neighbors[0]:
plt.scatter([x1[i][0], X_sample[0][0]], [x1[i][1], X_sample[0][1]], marker='o', c='b', s=100)
plt.show()
效果图:
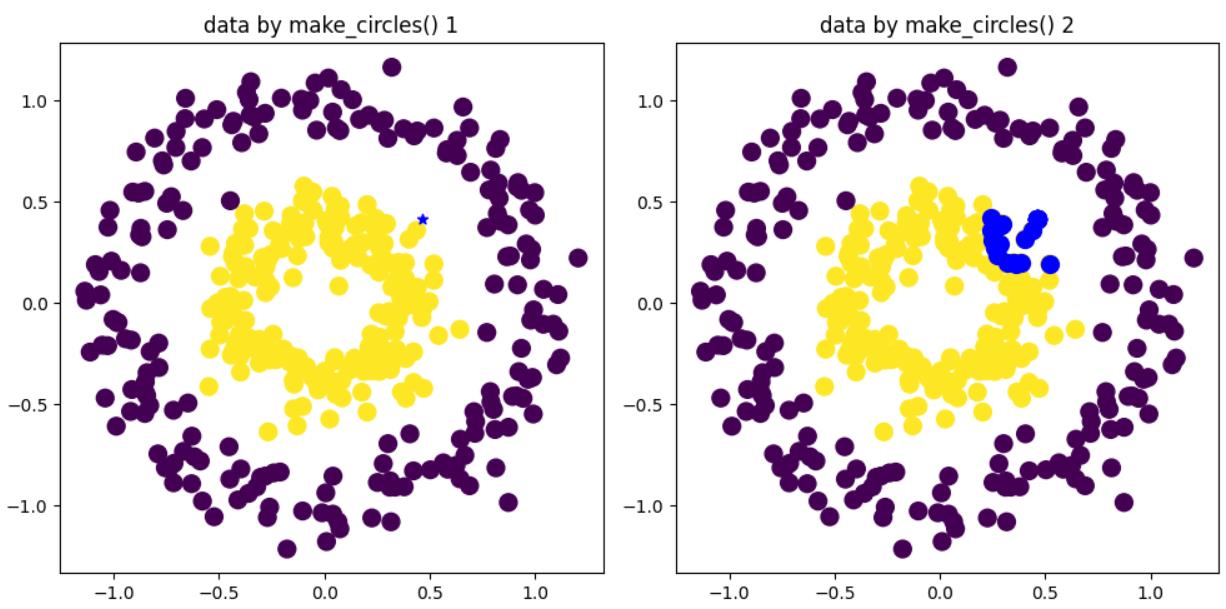
第二题:
Sklearn中的datasets方法导入训练样本,并用留一法产生测试样本,用KNN分类并输出分类精度。
"""
Sklearn中的datasets方法导入训练样本
并用留一法产生测试样本
用KNN分类并输出分类精度
"""
import warnings
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import LeaveOneOut
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore') # 忽略warning
iris = datasets.load_iris()
X = iris.data
y = iris.target
loo = LeaveOneOut() # 留一法,将数据集划分为训练集和测试集
K = []
Accuracy = []
for k in range(1, 16): # 将k从1到16结束。
correct = 0
knn = KNeighborsClassifier(k)
for train, test in loo.split(X): # 对测试机和训练集进行分割
knn.fit(X[train], y[train]) # 初始化svm进行训练。
y_sample = knn.predict(X[test])
if y_sample == y[test]: # 如果是正确的就累积+1
correct += 1
K.append(k)
Accuracy.append(correct / len(X))
plt.plot(K, Accuracy)
plt.xlabel('Accuracy:')
plt.ylabel('K:')
print('K次数:{} Accuracy正确率:{}'.format(k, correct / len(X)))
plt.show()
输出结果:
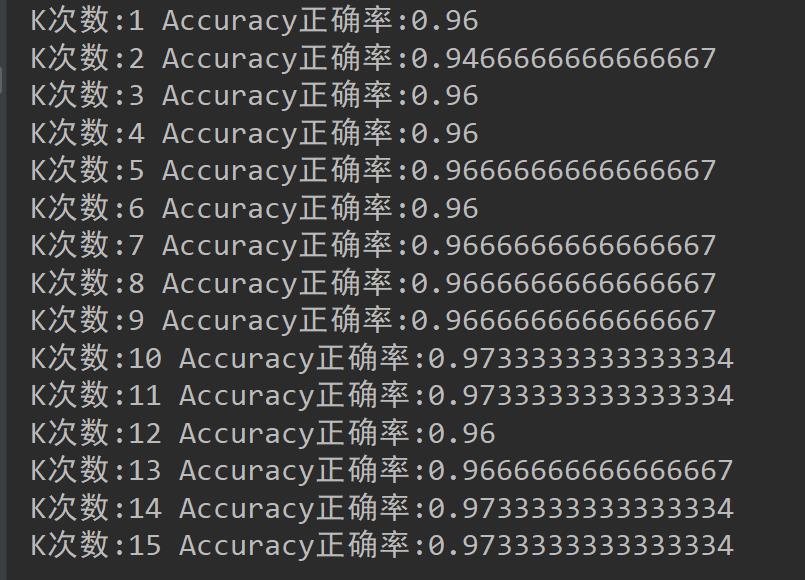
图像结果:
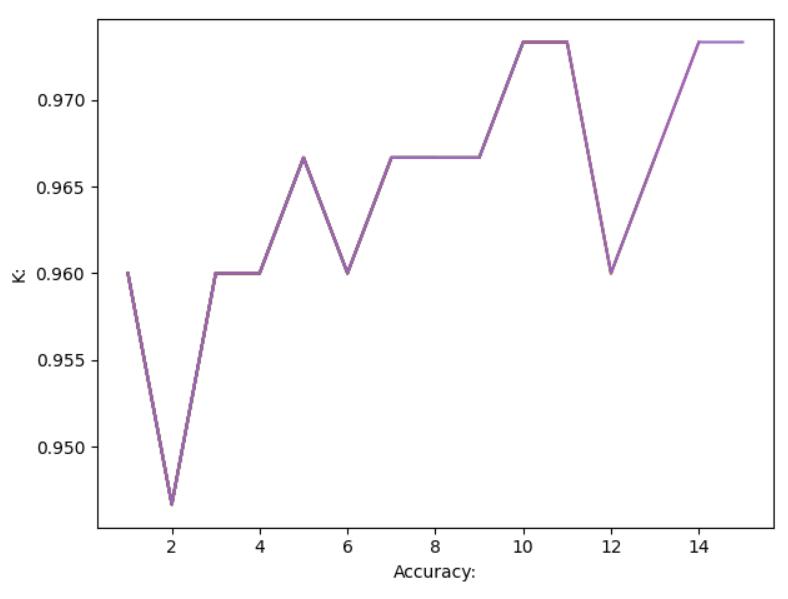
最后
小生凡一,期待你的关注
以上是关于机器学习入门 KNN分类算法 | 附加小练习的主要内容,如果未能解决你的问题,请参考以下文章