LeetCode 140. 单词拆分 II（回溯算法和DFS解决）

Posted 2021-09-16 数据结构和算法

截止到目前我已经写了 600多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

回溯算法解决

前面我们分别通过动态规划，DFS以及BFS三种方式来判断字符串是否可以拆分，具体可以看下

573，动态规划解单词拆分

574，DFS和BFS解单词拆分

今天这题不光要判断字符串是否可以拆分，如果可以拆分还要打印所有可能的拆分结果。判断是否可拆分比较简单，我们直接使用第573题动态规划的方式来判断即可，如果不能拆分我们直接返回一个空的集合，如果可以拆分我们就拆分。

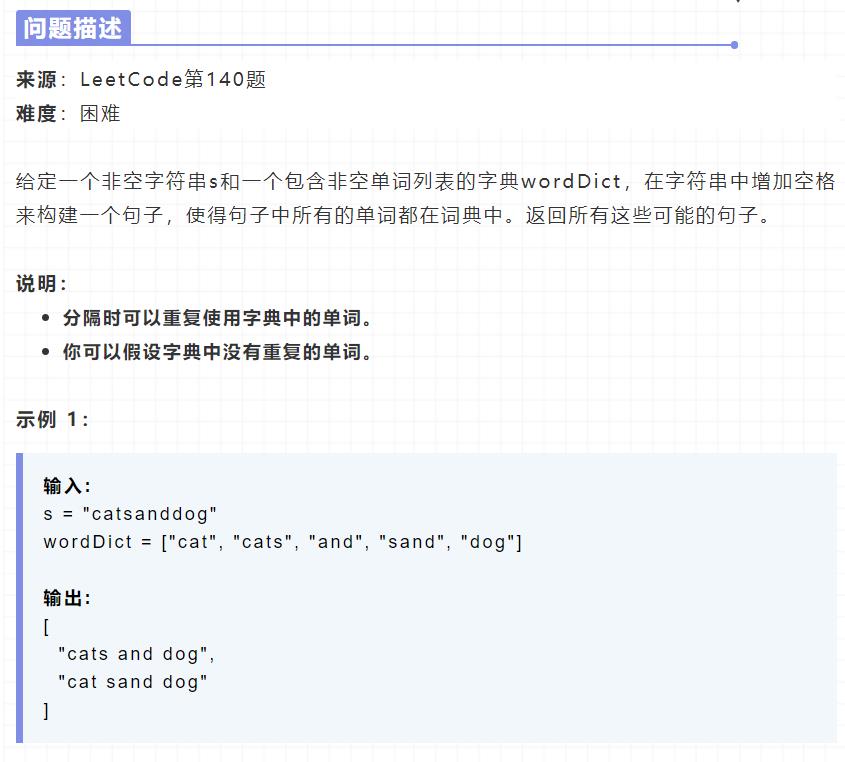
拆分的原理比较简单，我们逐渐截取子串，判断是否在字典中，如果不在字典中就继续截取更长的子串……，如果在字典中我们就沿着这个路径走下，如下图所示（这里是有两组结果，由于图画不下了，剩下的使用省略号没有画出来），我们可以把它看做是一棵n叉树

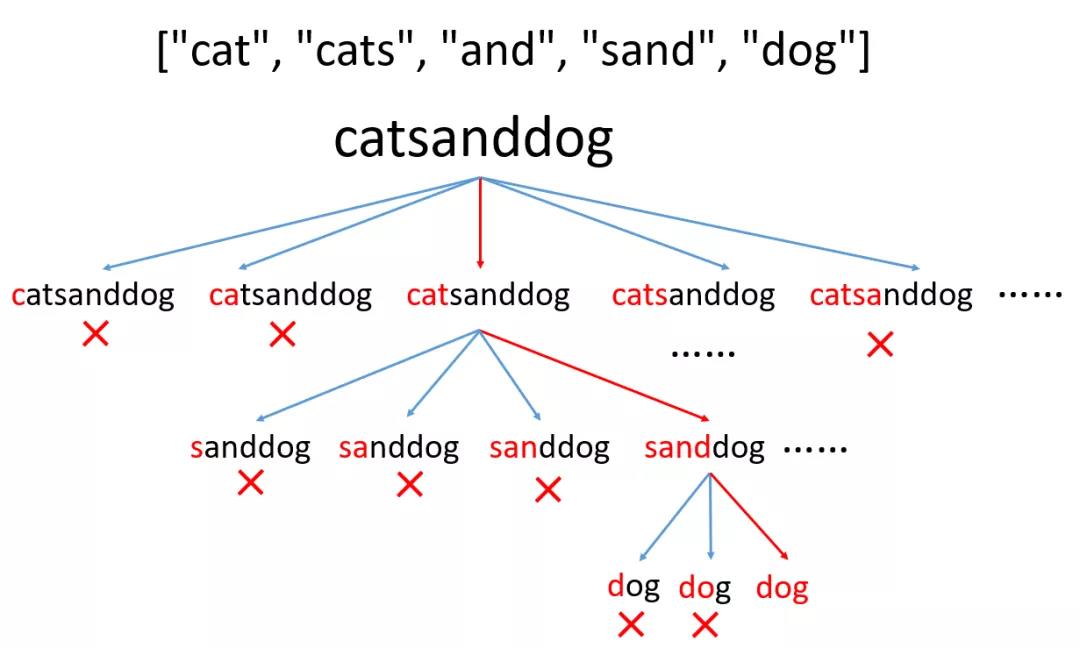
对于n叉树的路径我们可以使用回溯算法来解决，回溯算法我们之前也讲过很多次了，具体可以看下450，什么叫回溯算法，一看就会，一写就废，其实他有一个经典的模板

private void backtrack("原始参数") {
    //终止条件(递归必须要有终止条件)
    if ("终止条件") {
        //一些逻辑操作（可有可无，视情况而定）
        return;
    }

    for (int i = "for循环开始的参数"; i < "for循环结束的参数"; i++) {
        //一些逻辑操作（可有可无，视情况而定）

        //做出选择

        //递归
        backtrack("新的参数");
        //一些逻辑操作（可有可无，视情况而定）

        //撤销选择
    }
}

我们对这个模板稍微修改一下就是今天这题的答案，虽然这是一道hard题，但经过我们的逐步分析，发现也不是那么难，来看下代码

public List<String> wordBreak(String s, List<String> wordDict) {
    //集合Set的查找效率要比集合list高，这里为了提高效率，
    //先把list转化为集合set
    Set<String> set = new HashSet<>(wordDict);
    //下面是动态规划方式，判断字符串被拆解的子串是否都在字典中
    int length = s.length();
    boolean[] dp = new boolean[length + 1];
    dp[0] = true;//边界条件
    for (int i = 1; i <= length; i++) {
        for (int j = 0; j < i; j++) {
            dp[i] = dp[j] && set.contains(s.substring(j, i));
            if (dp[i]) {
                break;
            }
        }
    }
    List<String> res = new ArrayList<>();
    //如果不能拆解，直接返回空的集合就行了
    if (!dp[length])
        return res;
    //如果能被拆解，我们通过回溯方式执行拆解
    traceback(s, set, 0, res, new ArrayList<>());
    return res;
}

//回溯方式拆解字符串
private void traceback(String s, Set<String> wordDict, int start, List<String> res, List<String> path) {
    if (start == s.length()) {
        //下面这两行代码都是字符串加空格然后拼接，一个是官方提供的方法，
        //一个是我自己写的，都可以实现
        //res.add(String.join(" ", path));
        res.add(join(path));
        return;
    }
    for (int i = start + 1; i <= s.length(); i++) {
        //拆解字符串
        String str = s.substring(start, i);
        //如果拆解的子串不存在于字典中，就继续扩大子串
        if (!wordDict.contains(str))
            continue;
        //如果拆解的子串存在于字典中，就把子串添加到path中
        path.add(str);
        //往下继续递归
        traceback(s, wordDict, i, res, path);
        //执行回溯，把之前添加的子串给移除
        path.remove(path.size() - 1);
    }
}

//字符串加空格拼接
private String join(List<String> path) {
    StringBuilder stringBuilder = new StringBuilder();
    for (int i = 0; i < path.size(); i++) {
        stringBuilder.append(path.get(i));
        if (i != path.size() - 1)
            stringBuilder.append(" ");
    }
    return stringBuilder.toString();
}

DFS解决

回溯算法比较容易理解，这题我们还可以使用DFS来解决。比如我们进行截取的时候，如果截取的子串存在于字典中，我们通过递归的方式拆分剩下的，如果剩下的能够拆分我们就把当前拆分的子串和剩下拆分的结果进行拼接，如果剩下的不能拆分，不会进行任何拼接，直接返回空的集合即可，其实这种思路还可以借鉴《464. BFS和DFS解二叉树的所有路径》的最后一种解法，实现原理如下所示

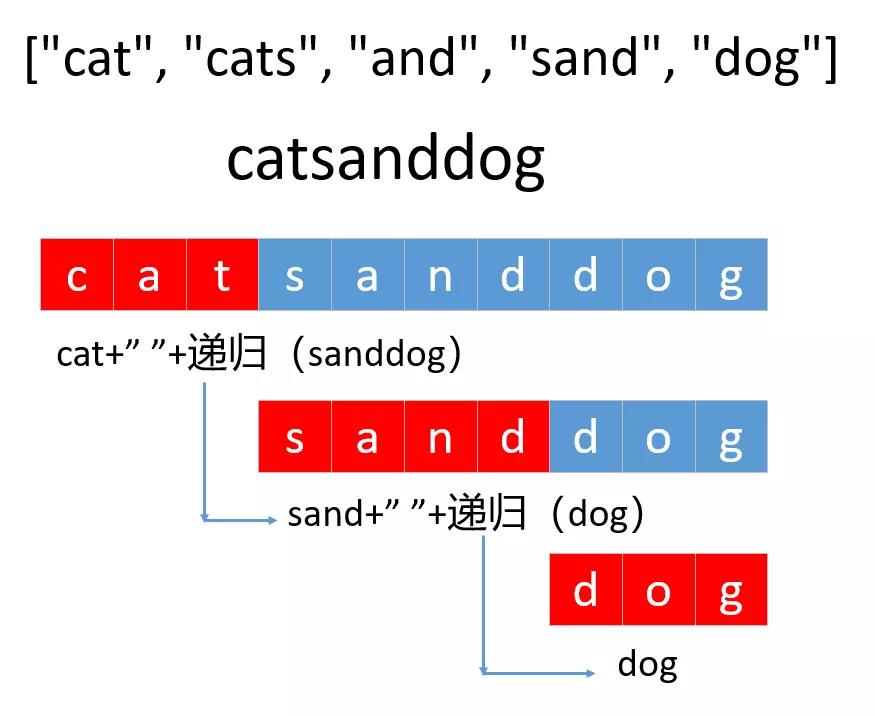
来看下代码

public List<String> wordBreak(String s, List<String> wordDict) {
    return backtrack(s, new HashSet<>(wordDict), 0);
}

public List<String> backtrack(String s, Set<String> wordDict, int start) {
    List<String> res = new ArrayList<>();
    for (int i = start + 1; i <= s.length(); i++) {
        String str = s.substring(start, i);
        //如果拆解的子串不存在于字典中，就继续拆
        if (!wordDict.contains(str))
            continue;
        //走到下面这个地方，说明拆分的子串str存在于字典中
        //如果正好拆完了，我们直接把最后一个子串添加到res中返回
        if (i == s.length())
            res.add(str);
        else {
            //如果没有拆完，我们对剩下的子串继续拆分
            List<String> remainRes = backtrack(s, wordDict, i);
            //然后用当前的子串str和剩下的子串进行拼接（注意如果剩下的子串不能
            //完全拆分，remainRes就会为空，就不会进行拼接）
            for (String remainStr : remainRes) {
                res.add(str + " " + remainStr);
            }
        }
    }
    return res;
}

我们知道递归必须要有终止条件的，但这题好像没有，其实是有的，当for循环不满足条件的时候，就不会再调用自己了。