字符串-回文自动机

Posted 2021-09-16 吾仄lo咚锵

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了字符串-回文自动机相关的知识，希望对你有一定的参考价值。

文章目录

原理
模板
例题

原理

回文自动机（Palindromes_Automaton，PAM），也叫回文树，是高效解决回文问题的算法，能够解决很多Manacher算法解决不了的回文题。可以解决如回文串个数、本质不同回文串个数、前缀0-i内回文串个数、某下标结尾的回文串个数等。

学习前建议先了解下字典树。

之所以还称之为回文树，是因为借鉴了字典树，希望可以压缩公共部分来存储所有回文子串情况。但和一般的树又有点不同，回文树有两个根节点，可以称为奇根和偶根，分别对应回文串是奇数和偶数的情况。如下图，每经过一条边，节点左右就加上边的值，以此作为建树的基础：

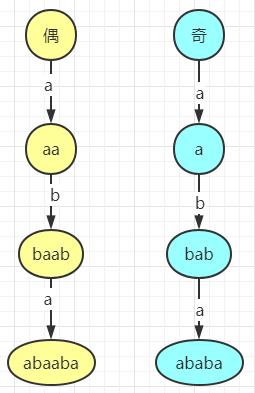
然后关键是怎么建树？现在只有一条字符串S。
我们定义0号节点为偶数长度根，1号节点为奇数长度根；

$f a i l [u]$ 点 $u$ 后缀边指向的点
$l e n [u]$ 点 $u$ 所表示的回文串长度
$t r i e [u] [c h]$ 点u前后各增加一个字符ch得到的点
$s t r [i]$ 是需要构造的串的第 $i$ 位
$c n t [i]$ 表示以 $i$ 结尾的回文串的个数
$l a s t$ 指向最长回文子串的右端点（必定存在，即一个字符情况）

对于 $l e n []$ 比较好理解， $l e n [0] = 0, l e n [1] = - 1$ ，0号偶数根置0，1号奇数根置-1，为了后续长度-1成为奇数，那对于其他子节点的长度，就是父节点的长度+2。

关键难点是构建 $f a i l []$ 指针，如果你有了解过AC自动机，就更好理解了。类似AC自动机，返回失配后与当前 $i$ 结尾的最长回文串本质上不同的最长回文后缀。
$f a i l$ 指针指向节点的最长回文后缀，所以在新加入一个字符时，要从当前节点不断的递推 $f a i l$ 指针，直到某一个节点所表示的回文串的两侧都能扩展一个待添加的字符while (str[idx] != str[idx - len[u] - 1])u = fail[u];。然后看这个节点有没有相应子节点，如果有就直接走下去，没有就新建一个节点（同字典树）。

注意下奇根和偶根的 $f a i l$ 指针，由于奇根的子节点表示的回文串长度为 1（即该字符本身），所以奇根相当于是可以向两侧扩展任意字符的，所以把偶根的 $f a i l$ 指针指向奇根。

当 $s t r [i - l e n [l a s t] - 1] \neq = s t r [i]$ 时，即 $i - 1$ 的最长回文串无法通过前后拓展一个字符S[i]形成更长的回文串，则将 $l a s t$ 设为 $f a i l [l a s t]$ ，寻找它的最长回文后缀，最终一定能找到。

模板

struct PAM {
    int size, last, r0, r1;
    int trie[maxn][26], fail[maxn], len[maxn], cnt[maxn];
    PAM() {
        r0 = size++, r1 = size++; last = r1;
        len[r0] = 0, fail[r0] = r1;
        len[r1] = -1, fail[r1] = r1;
    }
    void insert(int ch, int idx) {
        int u = last;
        while (str[idx] != str[idx - len[u] - 1])u = fail[u];
        if (!trie[u][ch]) {
            int cur = ++size, v = fail[u];
            len[cur] = len[u] + 2;
            for (; str[idx] != str[idx - len[v] - 1]; v = fail[v]);
            fail[cur] = trie[v][ch]; trie[u][ch] = cur;
            cnt[cur] = cnt[fail[cur]] + 1;
        }
        last = trie[u][ch];
    }
    void build(char* str) {
        int len = strlen(str);
        for (int i = 0; i < len; i++) 
            insert(str[i] - 'a' + 1, i);
    }
}pam;

例题

P5496 【模板】回文自动机（PAM）

题目背景
模板题，无背景（其实是我想不出背景）。
题目描述
给定一个字符串 ss。保证每个字符为小写字母。对于s的每个位置，请求出以该位置结尾的回文子串个数。
这个字符串被进行了加密，除了第一个字符，其他字符都需要通过上一个位置的答案来解密。
具体地，若第i(i≥1) 个位置的答案是k，第i+1个字符读入时的ASCIIASCII 码为c，则第i+1 个字符实际的ASCII 码为(c−97+k)mod26+97。所有字符在加密前后都为小写字母。
输入格式
一行一个字符串s表示被加密后的串。
输出格式
一行， |s|个整数。第i个整数表示原串以第i个字符结尾的回文子串个数。
输入输出样例
输入 #1
debber
输出 #1
1 1 1 2 1 1
输入 #2
lwk
输出 #2
1 1 2
输入 #3
lxl
输出 #3
1 1 1
说明/提示
对于100%的数据，1≤∣s∣≤5×10⁵

求每个点结尾的回文数，即打印 $c n t []$

（~~插播反爬信息~~ ）博主CSDN地址：https://wzlodq.blog.csdn.net/

#include<bits/stdc++.h>
using namespace std;
const int maxn = 500005;
char str[maxn];
struct PAM {
    int size, last, r0, r1;
    int trie[maxn][26], fail[maxn], len[maxn], cnt[maxn];
    PAM() {
        r0 = size++, r1 = size++; last = r1;
        len[r0] = 0, fail[r0] = r1;
        len[r1] = -1, fail[r1] = r1;
    }
    void insert(int ch, int idx) {
        int u = last;
        while (str[idx] != str[idx - len[u] - 1])u = fail[u];
        if (!trie[u][ch]) {
            int cur = ++size, v = fail[u];
            len[cur] = len[u] + 2;
            for (; str[idx] != str[idx - len[v] - 1]; v = fail[v]);
            fail[cur] = trie[v][ch]; trie[u][ch] = cur;
            cnt[cur] = cnt[fail[cur]] + 1;
        }
        last = trie[u][ch];
    }
    void build(char* str) {
        int len = strlen(str);
        for (int i = 0; i < len; i++) {
            insert(str[i] - 'a' + 1, i);
            str[i + 1] = (str[i + 1] - 97 + cnt[last]) % 26 + 97;
            printf("%d ", cnt[last]);
        }
    }
}pam;
int main(){
    scanf("%s", str);
    pam.build(str);
    return 0;
}

SP7586 NUMOFPAL - Number of Palindromes

题意翻译
求一个串中包含几个回文串
输入输出样例
输入 #1
malayalam
输出 #1
15
说明/提示
0 < |s| <= 1000

统计 $c n t []$ 即可

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100005;
char str[maxn];
struct PAM {
    int size, last, r0, r1;
    int trie[maxn][26], fail[maxn], len[maxn], cnt[maxn];
    PAM() {
        r0 = size++, r1 = size++; last = r1;
        len[r0] = 0, fail[r0] = r1;
        len[r1] = -1, fail[r1] = r1;
    }
    void insert(int ch, int idx) {
        int u = last;
        while (str[idx] != str[idx - len[u] - 1])u = fail[u];
        if (!trie[u][ch]) {
            int cur = ++size, v = fail[u];
            len[cur] = len[u] + 2;
            for (; str[idx] != str[idx - len[v] - 1]; v = fail[v]);
            fail[cur] = trie[v][ch]; trie[u][ch] = cur;
            cnt[cur] = cnt[fail[cur]] + 1;
        }
        last = trie[u][ch];
    }
    void build(char* str) {
        int len = strlen(str);
        for (int i = 0; i < len; i++) 
            insert(str[i] - 'a' + 1, i);
    }
}pam;
int main(){
    scanf("%s", str);
    pam.build(str);
    int ans = 0;
    for (int i = 1; i <= pam.size; i++)
        ans += pam.cnt[i];
    printf("%d", ans);
    return 0;
}

P3649 [APIO2014]回文串

题目描述
给你一个由小写拉丁字母组成的字符串 s。我们定义s的一个子串的存在值为这个子串在s中出现的次数乘以这个子串的长度。
对于给你的这个字符串s，求所有回文子串中的最大存在值。
输入格式
一行，一个由小写拉丁字母（a~z）组成的非空字符串 s。
输出格式
输出一个整数，表示所有回文子串中的最大存在值。
输入输出样例
输入 #1
abacaba
输出 #1
7
输入 #2
www
输出 #2
4
说明/提示
【样例解释1】
用 s∣表示字符串s的长度。
一个字符串s₁s₂ …s_∣s∣的子串是一个非空字符串 s_i s_i+1s_j，其中1≤i≤j≤∣s∣。每个字符串都是自己的子串。
一个字符串被称作回文串当且仅当这个字符串从左往右读和从右往左读都是相同的。
这个样例中，有7个回文子串 a，b，c，aba，aca，bacab，abacaba。他们的存在值分别为 4, 2, 1, 6, 3, 5, 74,2,1,6,3,5,7。
所以回文子串中最大的存在值为 77。
第一个子任务共 8 分，满足1≤∣s∣≤100。
第二个子任务共 15 分，满足1≤∣s∣≤1000。
第三个子任务共 24 分，满足1≤∣s∣≤10000。
第四个子任务共 26 分，满足1≤∣s∣≤100000。
第五个子任务共 27 分，满足1≤∣s∣≤300000。

对于第二个样例www，回文子串ww只记录了一次，因为是在回文树中增量加节点，所以构建时将cnt加一，并从叶节点往上累加统计cnt[fail[i]] += cnt[i]

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 300005;
char str[maxn];
struct PAM {
    int size, last, r0, r1;
    int trie[maxn][26], fail[maxn], len[maxn], cnt[maxn];
    PAM() {
        r0 = size++, r1 = size++; last = r1;
        len[r0] = 0, fail[r0] = r1;
        len[r1] = -1, fail[r1] = r1;
    }
    void insert(int ch, int idx) {
        int u = last;
        while (str[idx] != str[idx - len[u] - 1])u = fail[u];
        if (!trie[u][ch]) {
            int cur = ++size, v = fail[u];
            len[cur] = len[u] + 2;
            for (; str[idx] != str[idx - len[v] - 1]; v = fail[v]);
            fail[cur] = trie[v][ch]; trie[u][ch] = cur;
        }
        last = trie[u][ch];
        cnt字符串-回文自动机
 字符串-回文自动机
 131. 分割回文串
 回文自动机例题
 回文自动机学习笔记
 PAM / 回文自动机（回文树）略解