数学建模 层次分析法

Posted 2021-09-15 DQ_CODING

简介

针对多目标,多准则或无结构特性的复杂决策问题

步骤

解决评价类问题

评价类问题:

资料查找:
1)查找相关文献

2)如果没有找到相关文献

3)搜索

通过上述步骤后得到的结果

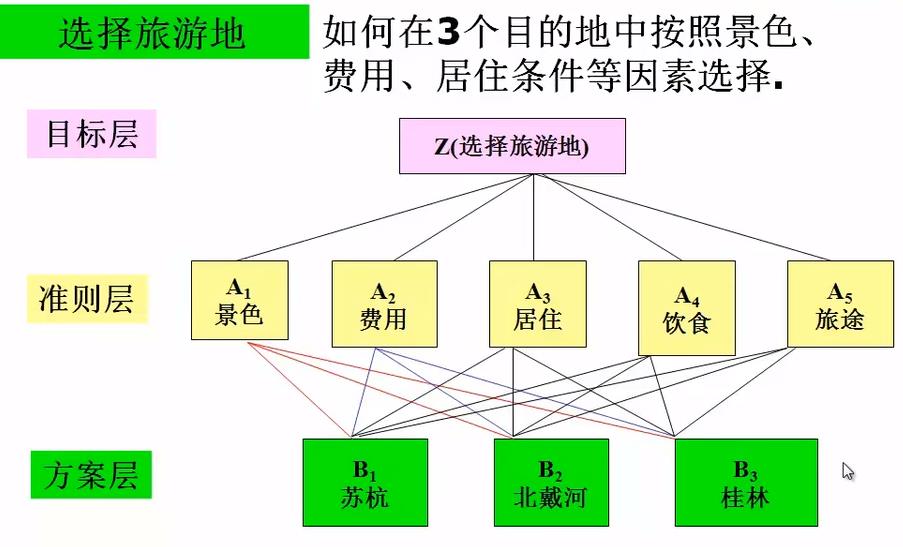
构建层次结构模型

举例:

成对比较矩阵

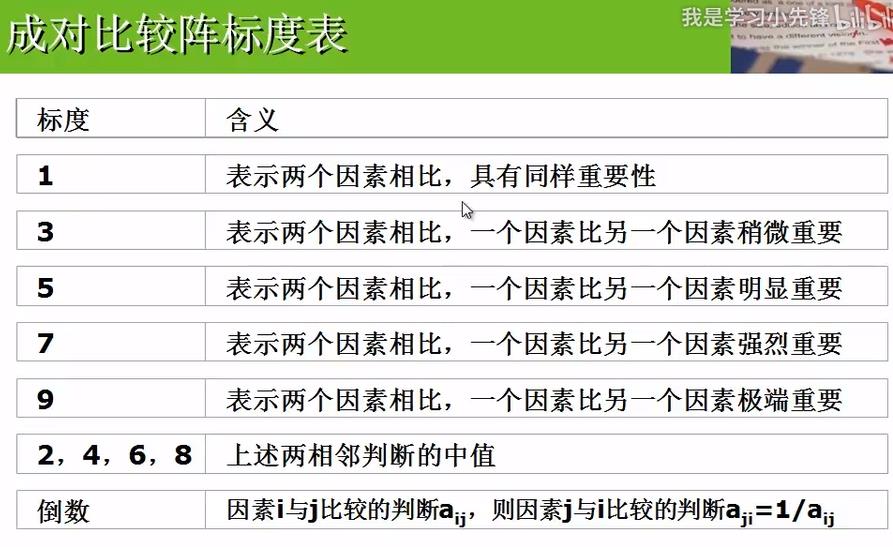
标度表:
奇数:越大越重要
偶数:上述两相邻判断的中值
倒数:aji=1/aij

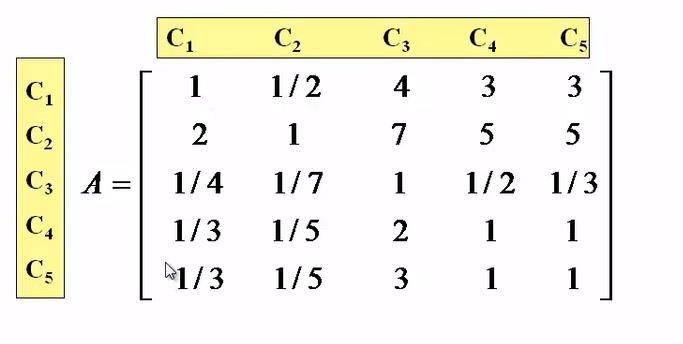
展示:
行列:
C1C1=1 C1与C1同样重要
C1C2=1/2 C2比C1重要
C1C3=4 C1比C3重要

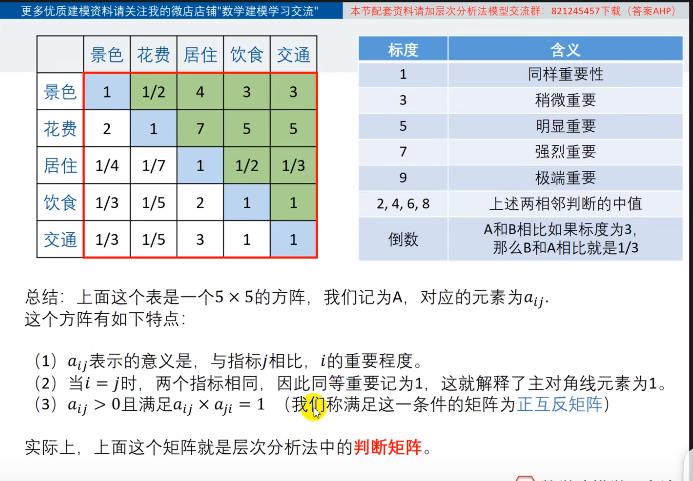
一致性检验

正反矩阵:

一致性矩阵:

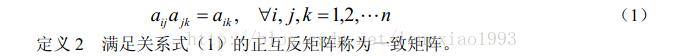
一致性检验:
在使用判断矩阵之前要先进行一致性检验

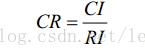
一致性的检验是通过计算一致性比例CR 来进行的
当 CR<0.10 时，认为判断矩阵的一致性是可以接受的，否则应对判断矩阵作适当修正。
CI的值由判断矩阵计算获得，RI的值查表获得

举例-旅游问题

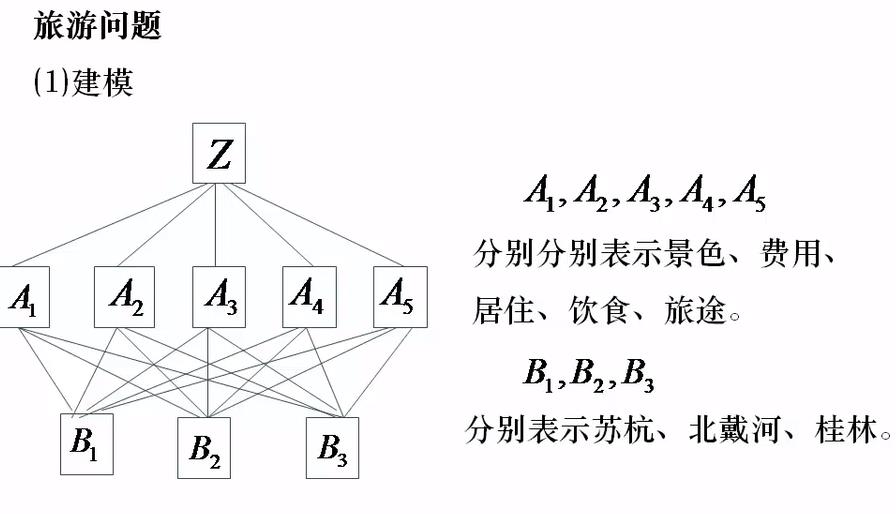
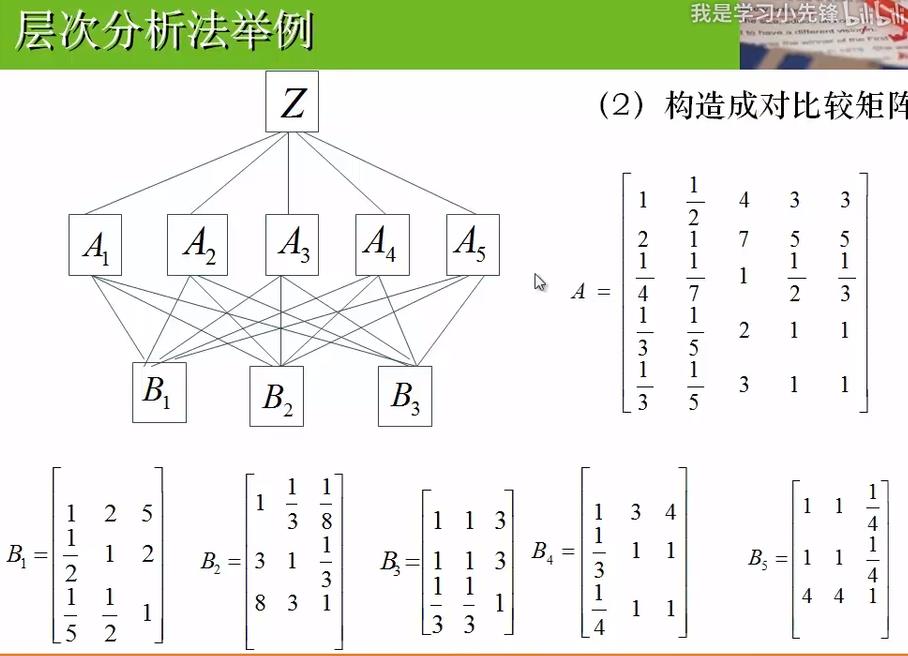
构造成对比较矩阵
1)A1-A5对Z的重要性的成对比较,所以有一个A矩阵(Z)
A:行[A1-A5] 列[A1-A5]
2)B1-B3在A1-A5这个层面上的比较,所以有5个B矩阵(A1-A5)
B:行[B1-B3] 列[B1-B3]

权重:
计算权重
第一行的和除以所有数的和得到a1。
第二行的和除以所有数的和 得到a2。
第三行的和除以所有数的和 得到a3。
同理，得到a4，a5。然后。
w1=a1/(a1+a2+a3+a4+a5)。
w2=a2/(a1+a2+a3+a4+a5)。
同理得到w3 w4 w5。

如:B1对A1的权重
a1=(1+2+5)/(1+2+5+…)=0.6060606060606061
w1=a1/(a1+a2+a3+a5)

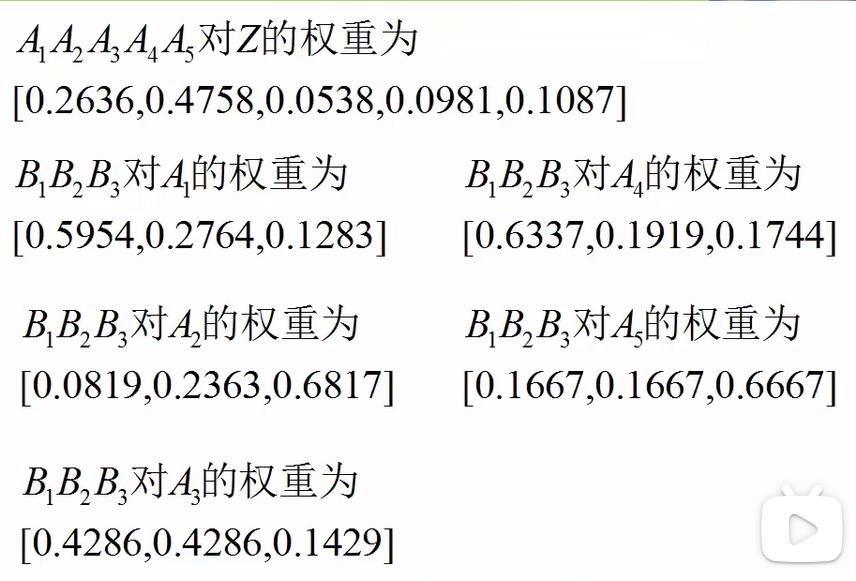
决策层对总目标的权向量
B1对Z的权值=B1对A1的权重A1对Z的权重+B1对A2的权重A2对Z的权重+…

结论:

程序(可作为模板套入)

输入矩阵A与B1-B5

[1, 1/2, 4, 3, 3;
 2, 1,   7, 5, 5;
 1/4, 1/7, 1, 1/2, 1/3;
 1/3, 1/5, 2, 1, 1;
 1/3, 1/5, 3, 1, 1;]

[1,2,5;
1/2,1,2;
1/5,1/2,1;]

[1,1/3,1/8;
3,1,1/3;
8,3,1;]

[1,1,3;
1,1,3;
1/3,1/3,1;]

[1,3,4;
1/3,1,1;
1/4,1,1;]

[1,1,1/4;
 1,1,1/4;
 4,4,1;]

matlab代码:

disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while  k>p
  i=i+1;
  x(:,i)=A*y(:,i-1);
  m(i)=max(x(:,i));
  y(:,i)=x(:,i)/m(i);
  k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);
         %以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10
    disp('此矩阵的一致性可以接受!');
    disp('CI=');disp(CI);
    disp('CR=');disp(CR);
end