数据结构学习笔记（二叉树）总结与整理

Posted 康x呀

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构学习笔记（二叉树）总结与整理相关的知识，希望对你有一定的参考价值。

数据结构学习笔记（二叉树）总结与整理

二叉树定义

概念：一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点：

  1. 每个结点最多有两棵子树，即二叉树不存在度大于2的结点。
  2. 二叉树的子树有左右之分，其子树的次序不能颠倒。
    二叉树的存储结构
    二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构
    二叉树的性质
  3. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
  4. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h- 1.
  5. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0＝n2＋1
  6. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=Log2(n+1). (ps：Log2(n+1)是log以2为底，n+1为对数)
  7. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：
  8. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
  9. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
  10. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

二叉树结构

数据结构中的二叉树：

结构定义：

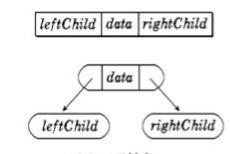
代码表示：

二叉树结构体定义：

// An highlighted block
//结点结构
typedef struct BinTreeNode
{
	ElemType data;
	struct BinTreeNode *leftChild;
	struct BinTreeNode *rightChild;
}BinTreeNode;
//根节点管理
typedef  BinTreeNode* BinTree;
void BinTreeInit(BinTree *t);

二叉树常用操作

**初始化**

// An highlighted block
void BinTreeInit(BinTree *t)
{
	*t = NULL;
}

二叉树的创建

二叉树创建——**使用指针引用方式**

// An highlighted block
void BinTreeCreate_1(BinTree *t)
{
	ElemType item;//接收数据
	scanf("%c", &item);
	if(item == '#')//判断输入是否为一个结束标记
		*t = NULL;//是 说明这棵二叉树是空树
	else
	{
		*t = (BinTreeNode*)malloc(sizeof(BinTreeNode));//创建树（子树）根结点
		assert(*t != NULL);
		(*t)->data = item;//为结点赋值
		BinTreeCreate_1(&(*t)->leftChild);//创建左子树
		BinTreeCreate_1(&(*t)->rightChild);//创建右子树
	}
}

二叉树创建——**通过返回值返回二叉树**

// An highlighted block
BinTree BinTreeCreate_2()
{
	BinTreeNode *t;
	ElemType item;//接收数据
	scanf("%c", &item);
	if(item == '#')//判断输入是否为一个结束标记
		return NULL;//返回空
	//创建树（子树）根结点
	t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
	assert(t != NULL);
	t->data = item;//为结点赋值
	t->leftChild = BinTreeCreate_2();//创建左子树
	t->rightChild = BinTreeCreate_2();//创建右子树
	return t;//返回所创建的树
}

二叉树创建——**使用二级指针**

// An highlighted block
void _BinTreeCreate(BinTreeNode **t)
{
	ElemType item;//接收数据
	scanf("%c", &item);
	if(item == '#')//判断输入是否为一个结束标记
		*t = NULL;//是 说明这棵二叉树是空树
	else
	{
	    //创建树（子树）根结点
		*t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
		assert(*t != NULL);
		(*t)->data = item;//为结点赋值
		_BinTreeCreate(&(*t)->leftChild);//创建左子树
		_BinTreeCreate(&(*t)->rightChild);//创建右子树
	}
}

**二叉树创建——**传入要创建的二叉树的串进行创建

// An highlighted block
BinTree BinTreeCreate_3(char *str)
{
	BinTreeNode *t;
	if(*str=='#' || *str=='\\0')//判断输入是否为一个结束标记
		return NULL;//是 说明这棵二叉树是空树
	//创建树（子树）根结点
	t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
	assert(t != NULL);
	t->data = *str;//为结点赋值
	t->leftChild = BinTreeCreate_3(++str);//创建左子树
	t->rightChild = BinTreeCreate_3(++str);//创建右子树
	return t;
}

**根据前序遍历和中序遍历来创建二叉树**

// An highlighted block
BinTree BinTreeCreate_VLR_LVR(char *VLR, char *LVR, int n)
{
	if(n == 0)
		return NULL;
	int k = 0;
	//利用先序序列，查找根在中序序列的位置
	while(VLR[0] != LVR[k])
		k++;
    //创建根
	BinTreeNode *t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
	assert(t != NULL);
	t->data = LVR[k];

	t->leftChild = BinTreeCreate_VLR_LVR(VLR+1, LVR, k);//创建t的左子树
	t->rightChild = BinTreeCreate_VLR_LVR(VLR+k+1, LVR+k+1, n-k-1);//创建右子树
	return t;
}

**根据中序和后序序列创建二叉树**

// An highlighted block
BinTree BinTreeCreate_LVR_LRV(char *LVR, char *LRV, int n)
{
    if(n == 0)
		t = NULL;
	else
	{
        //利用后序序列，查找根在中序序列的位置
		int k = 0;
		while(LRV[n-1] != LVR[k]) //后序需要从后往前找根
		   k++;
	    //创建根节点
        t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
		assert(t != NULL);
		t->data = LVR[k];
	    //递归创建右树
         BinTreeCreate_LVR_LRV(t->rightChild,LVR+k+1,LRV+k,n-k-1);
  	    //递归创建左树
         BinTreeCreate_LVR_LRV(t->leftChild,LVR,LRV,k);
	    //返回树
	    return t;
}

递归方式二叉树的遍历

**前序遍历**

// An highlighted block
void BinTreePreOrder(BinTree t)
{
	if(t != NULL)//树不为空
	{
		printf("%c ", t->data); //访问（子树）根结点
		BinTreePreOrder(t->leftChild);//访问左子树
		BinTreePreOrder(t->rightChild);//访问右子树
	}
}

**中序遍历**

// An highlighted block
void BinTreeInOrder(BinTree t)
{
	if(t != NULL)//树不为空
	{
		BinTreeInOrder(t->leftChild);//访问左子树
		printf("%c ", t->data); //访问（子树）根结点
		BinTreeInOrder(t->rightChild);//访问右子树
	}
}

**后序遍历**

// An highlighted block
void BinTreePostOrder(BinTree t)
{
	if(t != NULL)
	{
		BinTreePostOrder(t->leftChild);
		BinTreePostOrder(t->rightChild);
		printf("%c ", t->data); 
	}
}

**层次遍历**（需要用到队列结构）

// An highlighted block
void BinTreeLevelOrder(BinTree t)
{
	if(t != NULL)
	{
		LinkQueue Q;//创建队列
		LinkQueueInit(&Q);//对队列初始化
		LinkQueuePush(&Q, t);//将二叉树根结点（地址）入队
		while(!LinkQueueEmpty(&Q))//判断队列是否为空
		{
			BinTreeNode *node = LinkQueueFront(&Q);//取（子树）根结点（地址）
			LinkQueuePop(&Q);//将（子树）根结点（地址）出队
			printf("%c ", node->data);//打印出（子树）根结点的数据
			if(node->leftChild != NULL)//判断该结点的左树是否为空
				LinkQueuePush(&Q, node->leftChild);//否 将左子树（地址）入队
			if(node->rightChild != NULL) //判断该结点右子树是否为空
				LinkQueuePush(&Q, node->rightChild);//否 将右子树（地址）入队
		}
	}
}

非递归方式二叉树的遍历

**非递归方式二叉树的前序遍历**（需要用到栈结构）

// An highlighted block
void BinTreePreOrder_NoR(BinTree t)
{
	if(t != NULL)//判断二叉树是否为空
	{
		LinkStack st; //申请一个栈
		LinkStackInit(&st);//初始化栈
		LinkStackPush(&st, t);//将二叉树的根结点入栈
		while(!LinkStackEmpty(&st))//判断栈顶是否为空
		{//否
			BinTreeNode *p = LinkStackTop(&st);//获取栈顶结点
			LinkStackPop(&st);//出栈
			printf("%c ", p->data);//打印数据
			/*这里需要注意的是栈结构是先进后出的，所以后访问的结点先入栈*/
			if(p->rightChild != NULL)//判断右子树是否为空
				LinkStackPush(&st, p->rightChild); //否 入栈
			if(p->leftChild != NULL)//判断左子树是否为空
				LinkStackPush(&st, p->leftChild);//否 入栈
		}
	}
}

**非递归方式二叉树的中序遍历**（需要用到栈结构）

// An highlighted block
void BinTreeInOrder_NoR(BinTree t)
{
	if(t != NULL)//判断二叉树是否为空
	{//不空
		LinkStack st;//设置一个栈结构
		LinkStackInit(&st);//初始化栈

		do
		{
			while(t != NULL)
			{
				LinkStackPush(&st, t);//将根结点入栈
				t = t->leftChild;//位置下移
			}
			BinTreeNode *p = LinkStackTop(&st);
			LinkStackPop(&st);//获取栈顶元素
			printf("%c ", p->data);//打印数据
			if(p->rightChild != NULL)//判断右子树是否为空
				t = p->rightChild;//访问右子树
		}
		while(!LinkStackEmpty(&st) || t!=NULL);
	}
}

**非递归方式二叉树的后序遍历**（需要用到栈结构）

// An highlighted block
void BinTreePostOrder_NoR(BinTree t)
{
	if(t != NULL)
	{
		BinTreeNode *prev = NULL;
		LinkStack st;//申请一个栈
		LinkStackInit(&st);//初始化

		do
		{
			while(t != NULL)
			{
				LinkStackPush(&st, t);//入栈
				t = t->leftChild;//指向左子树的根结点
			}
			BinTreeNode *p = LinkStackTop(&st);//获取栈顶元素
			if(p->rightChild==NULL || prev==p->rightChild)
			{
				LinkStackPop(&st);//出栈
				printf("%c ", p->data);
				prev = p;
			}
			else
				t = p->rightChild;
		}while(!LinkStackEmpty(&st));
	}
}

二叉树的其他功能

**二叉树的结点个数**

// An highlighted block
size_t Size(BinTree t)
{
	if(t == NULL)
		return 0;	
	//左孩子＋右孩子节点数+根节点数
	return Size(t->leftChild) + Size(t->rightChild) + 1;
}

**二叉树的高度**

// An highlighted block
size_t Height(BinTree t)
{
	size_t left_h, right_h;
	if(t == NULL)//判断二叉树是否为空，是 记录高度为0
		return 0;
    //求取左子树高度
	left_h = Height(t->leftChild);
	right_h = Height(t->rightChild);//求取右子树高度
	//返回：该二叉树高度=左子树与右子树的最大高度+1
	return (left_h > right_h ? left_h : right_h) + 1;
}

**二叉树叶子节点个数**

// An highlighted block
size_t LeafSize(BinTree t)
{
	if(t == NULL)
		return 0;
	if(t->leftChild==NULL && t->rightChild==NULL)
		return 1;
	return LeafSize(t->leftChild) + LeafSize(t->rightChild);
}

**二叉树第K层结点个数**

// An highlighted block
size_t LevelKSize(BinTree t, int k)
{
	if(t == NULL)
		return 0;
	if(k == 1)
		return 1;
	return LevelKSize(t->leftChild, k-1) + LevelKSize(t->rightChild, k-1);
}

**查找二叉树结点**

// An highlighted block
BinTreeNode* Find(BinTree t, ElemType key)
{
	BinTreeNode *p;
	if(t==NULL || t->data==key)//判断二叉树为空且判断结点值是否等于key值
		return t;
		//或者可以这么写
		//if(t == NULL) //判断二叉树是否为空
		//return NULL; //是  说明不存在，返回空
	//if(t->data == key) //否 判断结点值是否等于key值
		//return t; //是  返回结点地址
	p = Find(t->leftChild, key);//查找左子树
	if(p != NULL)//判断是否找到
		return p;//找到  返回结点地址
	// 没找到
	return Find(t->rightChild, key);// 查找右子树，返回查找结果
}

**查找某结点的父结点**

// An highlighted block
BinTreeNode* Parent(BinTree t, BinTreeNode *p)
{
	BinTreeNode *ret;
	if(t==NULL || t->leftChild==p || t->rightChild==p)
		return t;
	ret = Parent(t->leftChild, p);//查找t的左子树
	if(ret != NULL)//判断左子树中是否找到满足条件的结点
		return ret;
	return Parent(t->rightChild, p);//否，查找右子树
}

**克隆二叉树**

// An highlight
以上是关于数据结构学习笔记（二叉树）总结与整理的主要内容，如果未能解决你的问题，请参考以下文章
 

 数据结构学习笔记（二叉树）OJ题总结与整理


 数据结构学习笔记（二叉树）OJ题总结与整理


 LeetCode与《代码随想录》二叉树篇：做题笔记与总结-JavaScript版


 数据结构与算法学习笔记 树


 数据结构与算法学习笔记 树


 数据结构与算法学习笔记 树