小曾带你深入浅出机器学习(小白入门必备,近3万字带你了解机器学习)
Posted 研行笔录
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了小曾带你深入浅出机器学习(小白入门必备,近3万字带你了解机器学习)相关的知识,希望对你有一定的参考价值。
初识机器学习
机器学习起源:上世纪50年代,1959年在IBM工作的Arthur Samuel设计了一个下棋程序,这个程序具有学习的能力,它可以在不断的对弈中提高自己。
机器学习方法:支持向量机,回归,决策树,随机森林,强化方法,集成学习,深度学习等
机器学习作用:一定程度上可以帮助人们完成一些数据预测,自动化,自动决策,最优化等初步替代脑力的任务。
机器学习 本质:对于一个任务及其表现的度量方法,设计一种算法,让算法能够提取中数据所蕴含的规律。
学习方式:
- 有监督学习:输入机器的数据是带有标签,已知数据和其一一对应的标签,训练一个预测模型,将输入数据映射到标签的过程。常用于分类和回归问题
- 无监督学习:输入数据是无标签的,是为了推断出数据的一些内在结构。常用于关联规则的学习以及聚类
- 半监督学习:输入数据部分有标签,部分无标签,可以用来进行预测。【常用于在有监督的分类算法中加入无标记样本来实现半监督分类】
- 弱监督学习:数据集的标签是不可靠的,主要指标记不正确、多种标记、标记不充分、局部标记等。已知数据和其一一对应的弱标签,训练一个智能算法,将输入数据映射到一组更强的标签的过程。
监督学习的步骤:
- 数据的创建和分类,(标注-划分测试和训练集)
- 数据增强(data Augmentation), 一般搜集的数据都包含有扰动信息,需要对数据进行增强。数据增强一般包括,图像旋转,平移,颜色变换,裁剪,仿射变换
- 特征工程(Feature Engineering), 包括特征提取和特征选择【提出的不同的网络结构、正则化、归一化方法实际上就是深度学习背景下的特征工程】
- 构建预测模型和损失 构建模型预测和标签之间的损失函数,常见的损失函数(Loss Function)有交叉熵、均方差等
- 训练, 选择合适的模型和超参数,通过合适的优化方法不断缩小输出与标签之间的差距【优化方法:梯度下降法及其变种】
- 验证和模型选择. 需要进行模型测试。利用验证集来验证模型是否可以准确地得出结果
- 测试和应用.
当有了一个准确的模型,就可以将该模型部署到你的应用程序中。
机器学习和数据挖掘傻傻分不清:
机器学习关心的问题是如何构建计算机程序使用经验自动改进
数据挖掘是从数据中提取模式的特定算法的应用,在数据挖掘中,重点在于算法的应用,而不是算法本身。
联系:数据挖掘是一个过程,在此过程中机器学习算法被用作提取数据集中的潜在有价值模式的工具。
入门分类回归算法
分类算法
分类(Classification)是机器学习的主要任务之一,分类算法是一种典型的监督学习算法,是根据样本的特征将样本划分到合适的类别中。具体来说就是利用训练样本来进行训练,从而得到样本特征到样本标签的映射,再利用该映射来得到新样本的标签,最终达到将样本划分到不同类别的目的。(二元分类问题、多元分类)
常见的几种分类模型有:线性模型、决策树模型、朴素贝叶斯模型、BP神经网络模型等。
回归算法
机器学习的另一个重要任务就是回归(Regression),回归算法同样也是一种监督学习算法。与分类问题不同的是,在分类算法中,样本标签是一些离散的值,每一种标签都代表着一个类别;然而在回归问题中,样本标签是一些连续的值。回归分析的目的是预测连续的数值型的目标值,接受一系列连续数据,寻找一个最适合数据的方程对特定的值进行预测。
常见的几种回归模型有:线性回归、广义线性回归、决策树回归、随机森林回归、岭回归、梯度提高树回归、生存回归、保序回归等。
注意:逻辑回归虽然叫回归算法,不是回归算法,是一种分类算法。
分类算法与回归算法区别
区别:**分类和回归最主要的区别就是输出的结果不同,定性输出称为分类,即离散变量的预测;定量输出称为回归,即连续变量的预测。**例如:预测一个人是小学生、中学生还是大学生,这是一个分类问题;预测一个人的年龄是多少岁,就是一个回归问题。
如何进行选择? 取决于对任务的分析和理解
常用分类算法的优缺点?
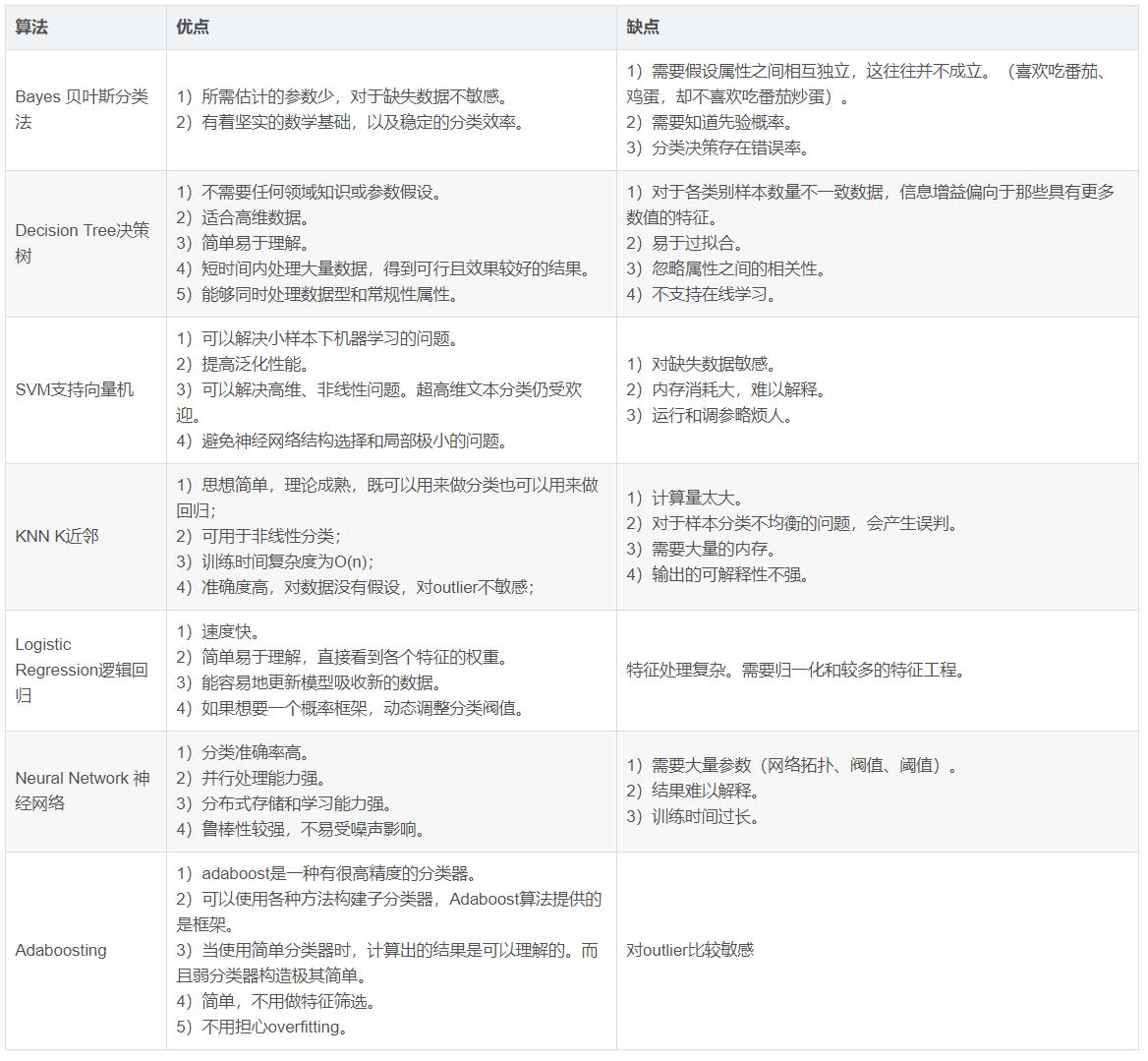
分类算法如何评估?
对于众多分类算法而言,需要一个评判标准来评估算法的好坏。主要从以下几种指标来进行评价
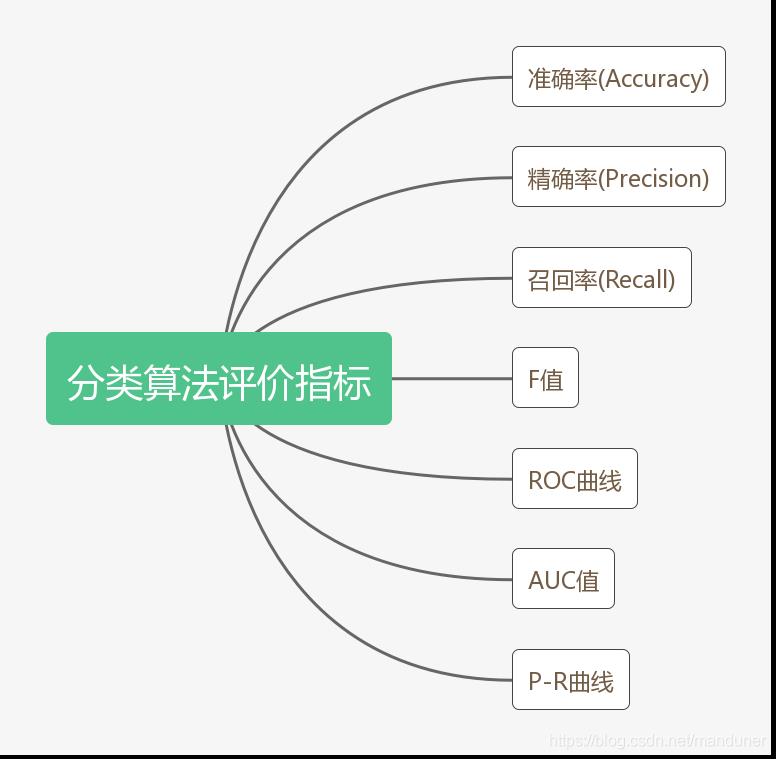
对于二分类问题而言,即将实例分成正类(positive)或负类(negative),在实际分类中会出现以下四种情况,具体如下图所示:
(1)若一个实例是正类,并且被预测为正类,即为真正类(True Positive TP)
(2)若一个实例是正类,但是被预测为负类,即为假负类(False Negative FN)
(3)若一个实例是负类,但是被预测为正类,即为假正类(False Positive FP)
(4)若一个实例是负类,并且被预测为负类,即为真负类(True Negative TN)
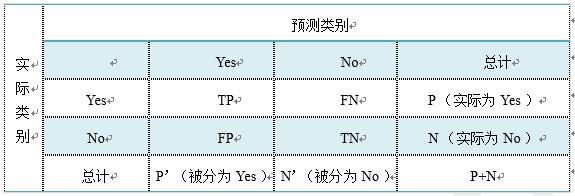
- 准确率(Accuracy):对于给定的测试数据集,分类器正确分类的样本数与总样本数之比。
Accuracy = T P + T N P + N \\text { Accuracy }=\\frac{T P+T N}{P+N} Accuracy =P+NTP+TN
缺点:在正负样本不平衡的情况下,这个指标有很大的缺陷。例如:给定一组测试样本共1100个实例,其中1000个是正类,剩余100个是负类。即使分类模型将所有实例均预测为正类,Accuracy也有90%以上,这样就没什么意义了. - 灵敏度(sensitivity):表示的是所有正例中被分对的比例,衡量了分类器对正例的识别能力。
recall = T P P \\text { recall }=\\frac{T P}{P} recall =PTP - 特异性(specificity):表示的是所有负例中被分对的比例,衡量了分类器对负例的识别能力。
recall = T N N \\text { recall }=\\frac{T N}{N} recall =NTN - 精确率(Precision):正确分类的正例个数占分类为正例的实例个数的比例[查准率]
precision = T P T P + F P \\text { precision }=\\frac{T P}{T P+F P} precision =TP+FPTP - 召回率(recall):正确分类的正例个数占实际正例个数的比例[查全率]
recall = T P T P + F N \\text { recall }=\\frac{T P}{T P+F N} recall =TP+FNTP - F1值:为了能够评价不同算法优劣,在Precision和Recall的基础上提出了F1值的概念,来对Precision和Recall进行整体评价。F1的定义如下: F 1 = 精确率 ∗ 召回率 ∗ 2 精确率 + 召回率 F 1=\\frac{\\text { 精确率 } * \\text { 召回率 } * 2}{\\text { 精确率 }+\\text { 召回率 }} F1= 精确率 + 召回率 精确率 ∗ 召回率 ∗2
- ROC曲线:是以灵敏度(真阳性率)为纵坐标,以1减去特异性(假阳性率)为横坐标绘制的性能评价曲线。可以将不同模型对同一数据集的ROC曲线绘制在同一笛卡尔坐标系中,ROC曲线越靠近左上角,说明其对应模型越可靠。也可以通过ROC曲线下面的面积(Area Under Curve, AUC)来评价模型,AUC越大,模型越可靠。
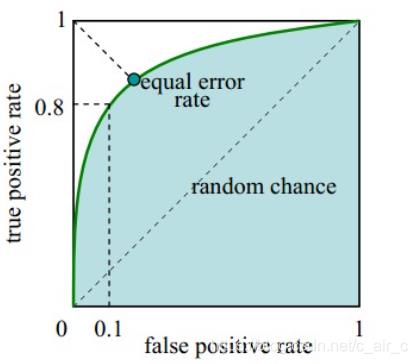
什么样的分类器是最优的?
希望的指标结果是的Precision越高越好,同时Recall也越高越好。但是这两个指标在某些情况下山有矛盾的。比如之前说的地震预测,既然不能百分百预测地震的发生,但实际情况中能容忍一定程度的误报。假设在1000次预测中,共有5次预测发生了地震,真实情况中有一次发生了地震,其他4次则为误报。正确率由原来的999/1000=99.9下降为996/1000=99.6。召回率由0/1=0%上升为1/1=100%。对此解释为,虽然预测失误了4次,但真的地震发生前,分类器能预测对,没有错过,这样的分类器实际意义更为重大,正是我们想要的。在这种情况下,在一定正确率前提下,要求分类器的召回率尽量高。
回归类型划分
广义线性模型家族里,依据因变量不同,可以有如下划分:
(1)如果是连续的,就是多重线性回归。
(2)如果是二项分布,就是逻辑回归。
(3)如果是泊松(Poisson)分布,就是泊松回归。
(4)如果是负二项分布,就是负二项回归。
(5)逻辑回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。所以实际中最常用的就是二分类的逻辑回归。
浅析逻辑回归
逻辑回归(LR)
概念:逻辑回归是应用非常广泛的一个分类机器学习算法,它将数据拟合到一个logit函数(或者叫做logistic函数)中,从而能够完成对事件发生的概率进行预测。
注意:声明的是逻辑回归是属于分类算法,最常用的就是二分类的逻辑回归。
优点:简单、可并行化、可解释强
逻辑回归和多重线性回归的区别:因变量不同【如果是连续的,就是多重线性回归;如果是二项分布,就是逻辑回归】
逻辑回归本质:假设数据服从这个分布,然后使用极大似然估计做参数的估计
逻辑回归的由来:追溯到线性回归
线性回归:对于多维空间中存在的样本点,我们用特征的线性组合去拟合空间中点的分布和轨迹
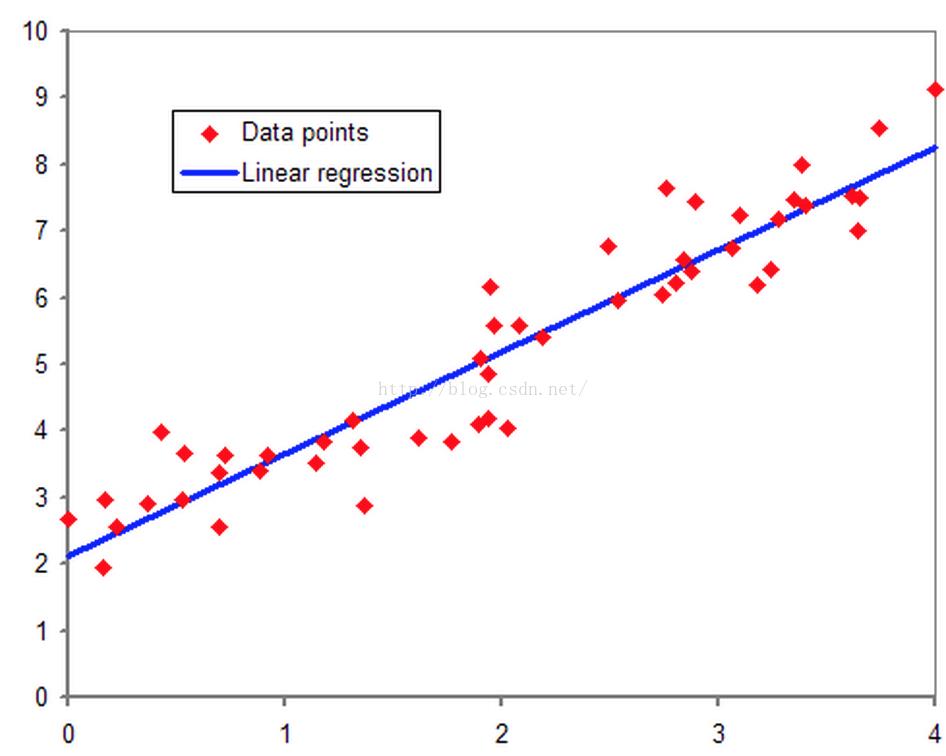
线性回归能对连续值结果进行预测,而现实生活中常见的另外一类问题是,分类问题。最简单的情况是是与否的二分类问题。比如说医生需要判断病人是否生病,银行要判断一个人的信用程度是否达到可以给他发信用卡的程度,邮件收件箱要自动对邮件分类为正常邮件和垃圾邮件等等。
当然,我们最直接的想法是,既然能够用线性回归预测出连续值结果,那根据结果设定一个阈值是不是就可以解决这个问题了呢?事实是,对于很标准的情况,确实可以的,这里我们套用Andrew Ng老师的课件中的例子,下图中X为数据点肿瘤的大小,Y为观测结果是否是恶性肿瘤。通过构建线性回归模型,如hθ(x)所示,构建线性回归模型后,我们设定一个阈值0.5,预测hθ(x)≥0.5的这些点为恶性肿瘤,而hθ(x)<0.5为良性肿瘤。
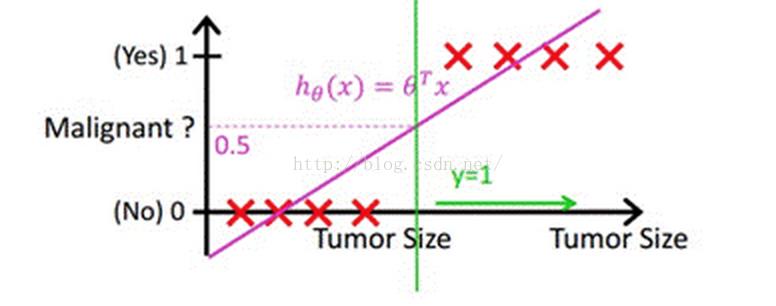
但很多实际的情况下,我们需要学习的分类数据并没有这么精准,比如说上述例子中突然有一个不按套路出牌的数据点出现,如下图所示:
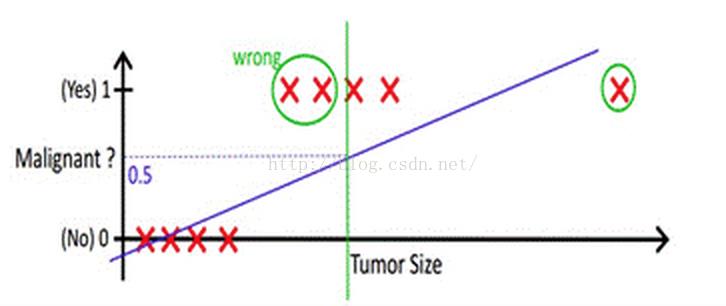
现在你再设定0.5,这个判定阈值就失效了,而现实生活的分类问题的数据,会比例子中这个更为复杂,而这个时候我们借助于线性回归+阈值的方式,已经很难完成一个鲁棒性很好的分类器了。
这样,逻辑回归就诞生了,它的核心思想是,如果线性回归的结果输出是一个连续值,而值的范围是无法限定的,那我们有没有办法把这个结果值映射为可以帮助我们判断的结果呢。而如果输出结果是 (0,1) 的一个概率值,这样就可以很清晰了。
线性回归与逻辑回归的区别
前面已经介绍过一些,现在进行总结一下
- 线性回归的样本的输出,都是连续值,在逻辑回归中 ,只能取0和1
- 对于拟合函数也有本质的区别
线性回归: f ( x ) = θ T x = θ 1 x 1 + θ 2 x 2 + … + θ n x n 逻辑回归: f ( x ) = P ( y = 1 ∣ x ; θ ) = g ( θ T x ) , 其中, g ( z ) = 1 1 + e − z ~ \\begin{aligned}&\\text { 线性回归: } f(x)=\\theta^{T} x=\\theta_{1} x_{1}+\\theta_{2} x_{2}+\\ldots+\\theta_{n} x_{n}\\\\&\\text { 逻辑回归: } f(x)=P(y=1 \\mid x ; \\theta)=g\\left(\\theta^{T} x\\right) \\text {, 其中, } g(z)=\\frac{1}{1+e^{-\\tilde{z}}} \\end{aligned} 线性回归: f(x)=θTx=θ1x1+θ2x2+…+θnxn 逻辑回归: f(x)=P(y=1∣x;θ)=g(θTx), 其中, g(z)=1+e−z~1
可以看出,线性回归的拟合函数,是对f(x)的输出变量y的拟合,而逻辑回归的拟合函数是对为1类样本的概率的拟合。
那么,为什么要以1类样本的概率进行拟合呢,为什么可以这样拟合呢?
θ T x = 0 \\theta^{T} x=0 θTx=0 就相当于是1类和0类的决策边界:
当 θ T x > 0 , 则 y > 0.5 ; 若 θ T x → + ∞ , 则 y → 1 , 即 y 为 1 类 ; 当 θ T x < 0 , 则 y < 0.5 ; 若 θ T x → − ∞ , 则 y → 0 , 即 y 为 0 类 ; \\begin{aligned} &\\text { 当 } \\theta^{T} x>0, \\text { 则 } y>0.5 ;若\\theta ^{T}x\\rightarrow +\\infty ,则y \\rightarrow 1 ,即y为1类; \\\\ &\\text { 当 } \\theta^{T} x<0, \\text { 则 } y<0.5 ;若 \\theta ^{T}x\\rightarrow -\\infty ,则y \\rightarrow 0,即y为0类; \\end{aligned} 当 θTx>0, 则 y>0.5;若θTx→+∞,则y→1,即y为1类; 当 θTx<0, 则 y<0.5;若θTx→−∞,则y→0,即y为0类;
这个时候就能看出区别,在线性回归中 θ T x \\theta^{T} x θTx 为预测值的拟合函数; 而在逻辑回归中 θ T x \\theta^{T} x θTx 为决策边界。下表2-3为线性回归和逻辑回归的区别。
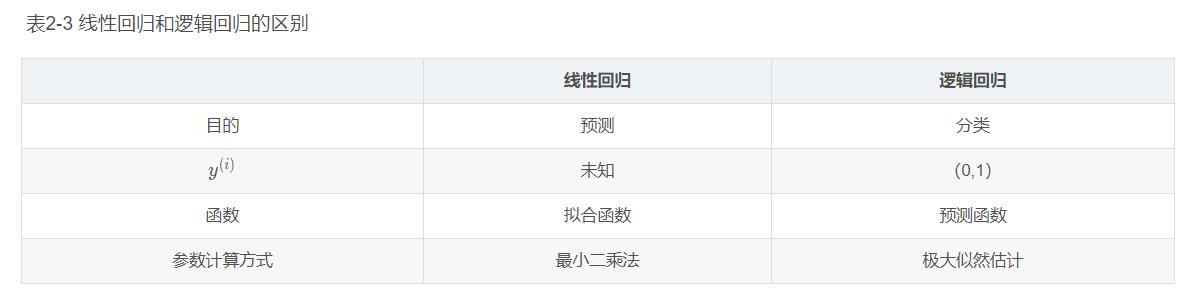
逻辑回归常规步骤
- 寻找h函数(即预测函数)
Logistic函数(或称为Sigmoid函数),函数形式为:以上是关于小曾带你深入浅出机器学习(小白入门必备,近3万字带你了解机器学习)的主要内容,如果未能解决你的问题,请参考以下文章