通宵爆肝：C语言下的平衡二叉树（Avl）原来如此简单！

Posted 2021-09-10 刘一哥GIS

文章目录

• 平衡二叉树的构造过程
• • 1 算法描述
• 平衡二叉树的编程
• • 1 树上结点的高度计算
  • 2 LL调整函数
  • 3 RR调整函数
  • 4 LR调整函数
  • 5 RL调整函数
  • 6 根据结点的值、动态构造平衡二叉树

---

平衡二叉树的构造过程

对一个查找问题而言，查找表的存储结构、应该组织成二叉树结构。而把一个离散的数据、组织成最接近满二叉排序树的方法，最常见的就是平衡二叉树。

对平衡二叉树而言，有四种调整方式，就是LL、LR、RR、RL四种方式。

1 算法描述

(1) LL调整

对图1而言，如插入10，就是下面的过程：

插入的结果就是：如40为根，则左子树高、减去右子树、高度差是2。在这种情况下，需要调整，调整的结果就是：注意K1、K2结点的变化。

(2) RR调整

对下面的树而言，插入80则发生RR调整：

对上述二叉树、进行调整就是下图的过程：注意K1、K2结点的变化。

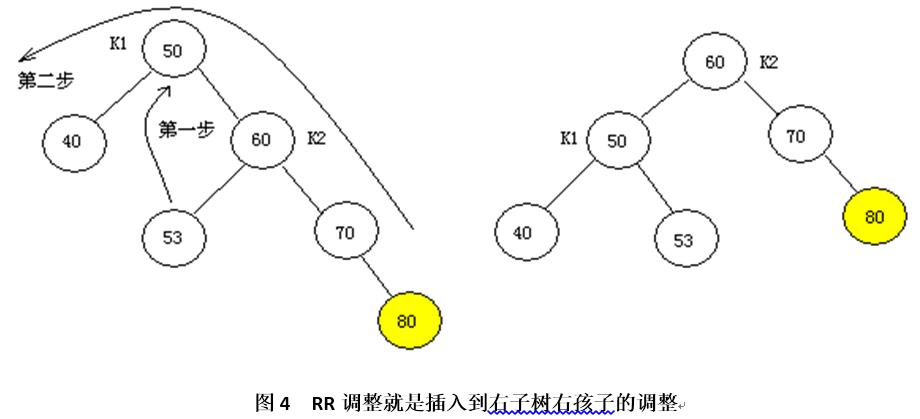
(3) LR调整

对以下的图，如果插入35，则要进行LR调整：

注意下面K3的变化：

.
(4) RL调整

在以下的树上，如果要插入53，则要进行的调整就是RL调整，注意过程：

此时要调整的过程、类似LR调整，过程如下：注意K1的变化。

平衡二叉树的四种调整介绍完毕，你能就任意一组数据、完成构造平衡二叉树的过程么？

平衡二叉树的编程

1 树上结点的高度计算

从前面的平衡二叉树的构造过程可知：对平衡二叉树，最关键的问题是结点的高度计算问题，如果每个结点的高度有了，则左右子树的高度差也就可以计算了。

我们从二叉排序树的结构中补充一个字段：Height，同时修改结构名称为AvlNode，目的就是构造平衡二叉树。

struct AvlNode
	{
	int Element;
	struct AvlNode  *Left;
	struct AvlNode  *Right;
	int    Height;
	};

我们定义：当前结点的高度、是取左右孩子高度最大值再加1，所以对一下的结点，有：

注意这个高度编法，它是从树的叶结点开始的，这样的高度计算方法和从树根编下来有差异，但计算左右树高度差都是一样的。之所以这么编高度，是因为编程中确定叶结点高度为0非常简单。

struct AvlNode *Insert(int X, struct AvlNode *T)
{
	if(T==NULL)
		{
		T =(struct AvlNode *)malloc(sizeof(struct AvlNode));
		if(T==NULL) {printf("内存不足\\n");exit(0);}
		T->Element=X; T->Left=T->Right= NULL;T->Height=0;
		}
	if(X<T->Element) T->Left=Insert(X,T->Left);
	if(X>T->Element) T->Right=Insert(X,T->Right);
	T->Height=Max(Height(T->Left), Height(T->Right))+1;
return T;
}

在表1的第7行，我们新构造的每个结点高度都是0；

在表1的第11行，当前结点T的高度是T的左、右孩子结点高度最大者加1，这样构造的树、其每个结点的高度就如同表9。

能插入结点值为X并构造二叉排序树的程序见AvlTree0.c，它能给每个结点计算高度，当然，这个程序还不能构造平衡二叉树，它依然构造的是二叉排序树。但我们知道：平衡二叉树是二叉排序树的一种特殊情况。我们就要根据这个程序，不断修改出一个能构造平衡二叉树的程序。

2 LL调整函数

LL调整函数的过程见图1、图2，首先我们给这个树从叶结点开始编高度，其高度数据就是：

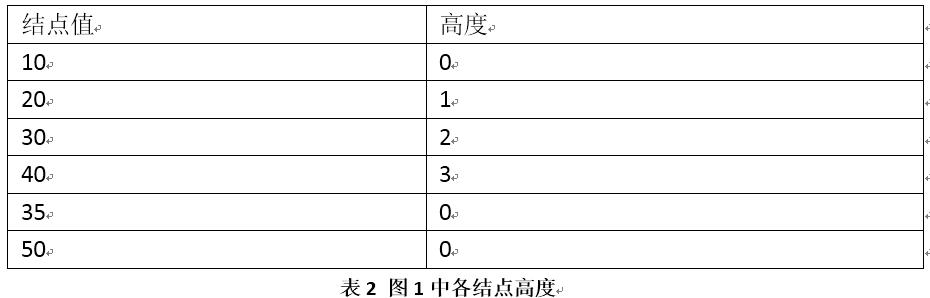
为测试方便，我们先编写main()函数、构造图1这样的二叉排序树，然后再编LL调整函数，所以main()就是：

main( )
{

    struct AvlNode *T;
    struct AvlNode BT[6];
    /*	构造图1的二叉排序树 */
    BT[0].Element=40;BT[0].Left=&BT[1];BT[0].Right=&BT[2];BT[0].Height=3;
    BT[1].Element=30;BT[1].Left=&BT[3];BT[1].Right=&BT[4];BT[1].Height=2;
    BT[2].Element=50;BT[2].Left=NULL;  BT[2].Right=NULL;BT[2].Height=0;  
    BT[3].Element=20;BT[3].Left=&BT[5];BT[3].Right=NULL;BT[3].Height=1;  
    BT[4].Element=35;BT[4].Left=NULL;  BT[4].Right=NULL;BT[4].Height=0;   
    BT[5].Element=10;BT[5].Left=NULL;  BT[5].Right=NULL;BT[5].Height=0;   
    T=LL(BT);
	jConvert(T);
	printf("\\n");
}

有这个二叉树后再次回顾图2，所谓LL调整就是：

如树的根为K2，则：

K1为K2的左孩子；

K2的左孩子赋值为K1的右孩子;(35给40当左孩子)

K1的右孩子赋值为K2;（40是35的右孩子）

调整K2的高度;

调整K1的高度;

返回K1为根的树；

用C语言写出来就是：

struct AvlNode *LL(struct AvlNode *K2)
{
struct AvlNode *K1;
K1 = K2->Left;
K2->Left = K1->Right;
K1->Right = K2;
//注意各个结点高度计算
K2->Height = Max(Height(K2->Left), Height(K2->Right))+1;
K1->Height = Max( Height(K1->Left), K2->Height)+1;
return K1;
}

全部代码见LL.C，以下结果看看是否合理。

ID PID Value Height
0 -1 30 2
1 0 20 1
2 1 10 0
3 0 40 1
4 3 35 0
5 3 50 0

一定尝试着用遍历的结果来反推这个树的形态。

3 RR调整函数

RR调整和LL调整是对称操作，看着图4，所以是：

如K1是根结点；

K2是K1的右孩子；

把K2的左孩子赋值给K1当右孩子(53成为50的右孩子)；

K1成为K2的左孩子(50成为60的左孩子)；

重新计算K1的高度；

重新计算K2的高度；

返回K2为根的二叉树；

所以程序见下表：

struct AvlNode * RR(struct AvlNode *K1)
{
struct AvlNode *K2;
K2 = K1->Right;
K1->Right = K2->Left;
K2->Left = K1;

K1->Height = Max(Height(K1->Left), Height(K1->Right))+1;
K2->Height = Max(Height(K2->Right), K1->Height)+1;
return K2;
}

对照表4，可知和LL调整是完全向对应、但方向相反。

下面是测试图4中RR调整的二叉树数据和main()程序

main( )
{

    struct AvlNode *T;
    struct AvlNode BT[6];
    /*  下面这组数据是测试RR平衡的 */
    BT[0].Element=50;BT[0].Left=&BT[1];BT[0].Right=&BT[2];BT[0].Height=3;   
    BT[1].Element=40;BT[1].Left=NULL;  BT[1].Right=NULL;  BT[1].Height=0;   
    BT[2].Element=60;BT[2].Left=&BT[3];BT[2].Right=&BT[4];BT[2].Height=2;   
    BT[3].Element=53;BT[3].Left=NULL;  BT[3].Right=NULL;  BT[3].Height=0;   
    BT[4].Element=70;BT[4].Left=NULL;  BT[4].Right=&BT[5];BT[4].Height=1;   
    BT[5].Element=80;BT[5].Left=NULL;  BT[5].Right=NULL;BT[5].Height=0;   
	T=RR(BT);
	jConvert(T);
	printf("\\n");
}

这个程序的结果见下表：

仔细分析以下这些结点的关系，尝试着用遍历的方法反推这个树的形态。

4 LR调整函数

从图6的过程可以看到：

所谓LR调整、如K3为根的话，则K3的左孩子先进行RR调整，然后，整个树再以K3为根做LL调整。
完成这样的调整、写成程序会非常简单，就是：

struct AvlNode *LR(struct AvlNode *K3)
{
		K3->Left = RR(K3->Left);
		return  LL(K3);
}

每个调整过程都会自己调整结点高度，所以整个LR调整中不需要再次调整结点高度。

5 RL调整函数

从图8的过程可知：

如树的根结点是K1，则首先K1的右孩子进行LL调整，调整后的结果，再按K1为根进行RR调整。
所以整个RL的调整编程就是：

struct AvlNode *RL(struct AvlNode *K1)
{
K1->Right=LL(K1->Right);
return RR(K1);
}

LR.C、LR.C两个函数的具体执行情况见相关程序。各个程序的结果请同学们自己分析。这样，我们就完成了平衡二叉树的结点高度定义、以及四种调整方法的函数，有了这些基础，我们再次修改Insert()函数就有基础了。

6 根据结点的值、动态构造平衡二叉树

回顾表1，这个函数仅仅能构造二叉排序树，经过修改，目前能对插入的结点计算出高度来，我们要不断修改这个函数，让它能构造平衡二叉树。

首先，当插入X后，要构造出二叉排序树，其次要立刻判断这个结点的高度差，在表1中，在当前结点T上插入结点（以插入左子树左孩子为例）后，就是：

if(X<T->Element) T->Left=Insert(X,T->Left);

但现在，首先要计算T的左右孩子高度差，如果高度差是2，则再次判断X是否小于T的左孩子，如是，则必然为LL调整，否则为LR调整，就是：

if(X<T->Element)
{
		T->Left = Insert(X,T->Left);
		if(Height(T->Left)-Height(T->Right)==2)
		if(X<T->Left->Element)
			T=LL(T);
		else
			T=LR(T);
}

注意上面的过程，是在X插入到当前结点T的左孩子的情况，此时，还有两种可能，在第5行的判断就是：插入到T的左孩子左子树，则做LL调整，如是在左孩子右子树，则做LR调整。同理可以编写出插入到右子树的情况，整个平衡二叉树的构造函数就是：

struct AvlNode *Insert(int X, struct AvlNode *T)
{
if(T==NULL)
	{
	T =(struct AvlNode *)malloc(sizeof(struct AvlNode));
	if(T==NULL) 
		{
		printf("内存不够，程序退出" );exit (0);
		}
    T->Element=X; T->Height=0;
    T->Left=T->Right= NULL;
	}
	if(X<T->Element)
		{
		T->Left = Insert(X,T->Left);
		if(Height(T->Left)-Height(T->Right)==2)
		if(X<T->Left->Element)
			T=LL(T);
		else
			T=LR(T);
		}
	if(X>T->Element)
		{
		T->Right = Insert(X,T->Right);
		if(Height(T->Right)-Height(T->Left)== 2)
			if(X>T->Right->Element )
				T=RR(T);
			else
				T=RL(T);
		}
T->Height=Max(Height(T->Left), Height(T->Right))+1;
return (T);
}

有这个函数后，我们可以编写个main()函数，测试这个函数是否正确，整个程序见AvlTree.c，这个程序用遍历的方法给出树的形态，注意自己再反推回去。