平衡二叉树AVL树定义插入以及调整最小不平衡子树（C语言）

Posted 2021-08-29 bfhonor

一、平衡二叉树定义

• 平衡二叉树（Balanced Binary Tree），简称平衡树（AVL树）——树上任一结点的左子树和右子树的高度之差不超过1。
• 结点的平衡因子=左子树高-右子树高。
  

//平衡二叉树结点
typedef struct AVLNode{
	int key;	//数据域
	int banlance;//平衡因子
	struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;

二、平衡二叉树的插入

• 在二叉排序树中插入新的结点后，如何保持平衡？？
  
  

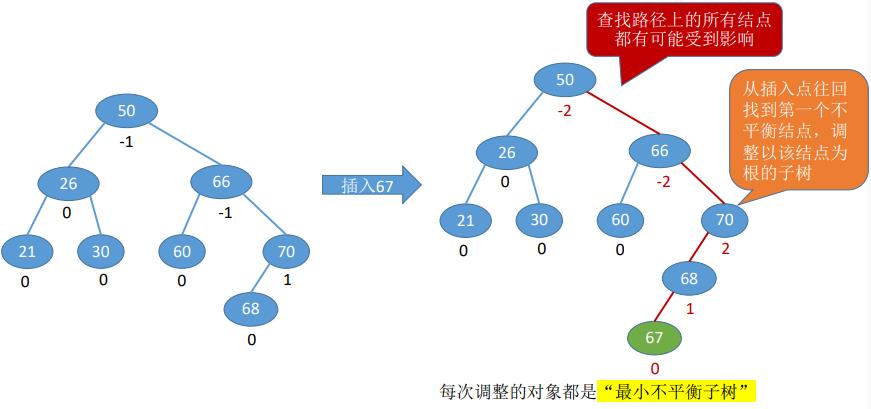
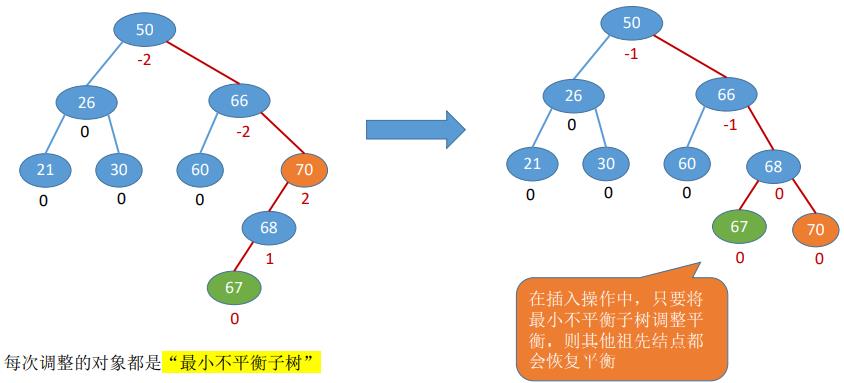
三、调整最小不平衡子树

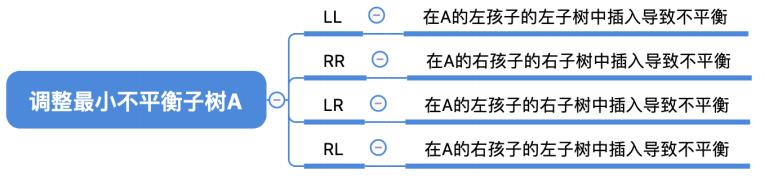
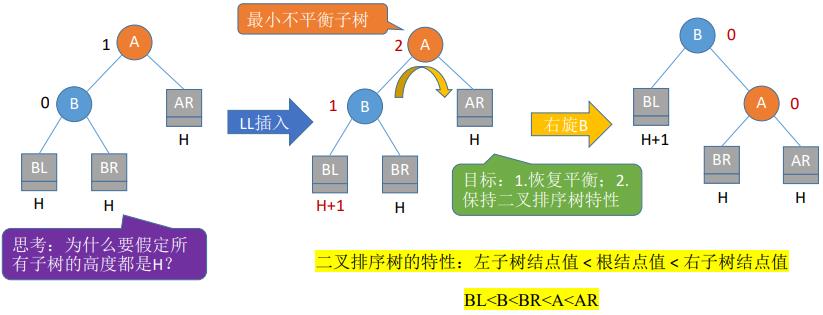
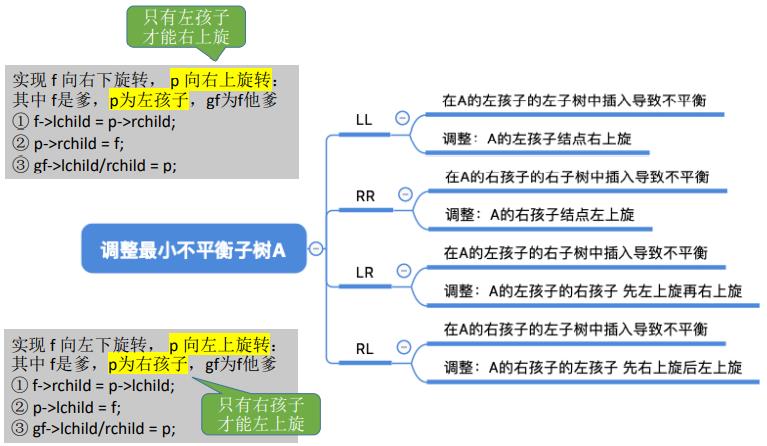
（一）调整最小不平衡子树（LL）

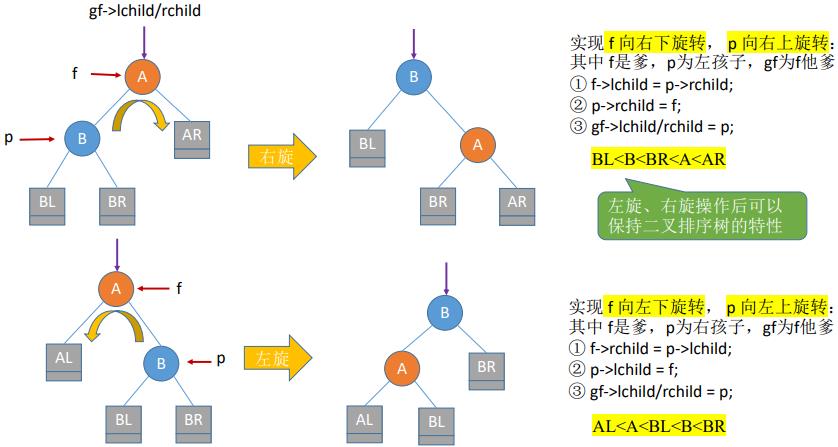
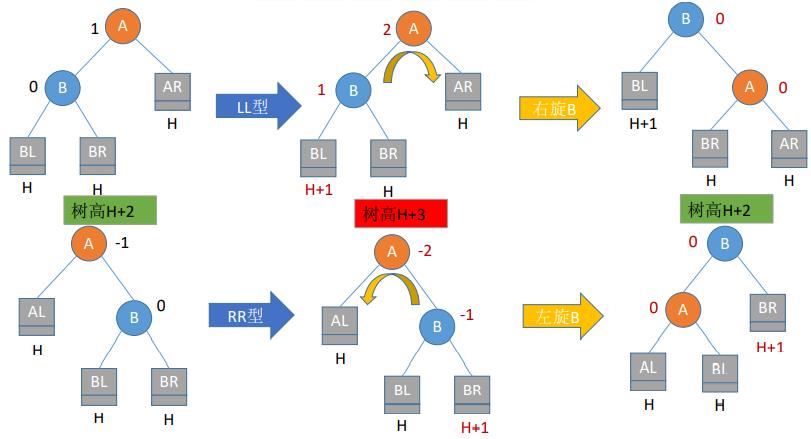
• （1）LL平衡旋转（右单旋转）。由于在结点A的左孩子（L）的左子树（L）上插入了新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点，将A结点向右下旋转成为B的右子树的根结点，而B的原右子树则作为A结点的左子树。
  

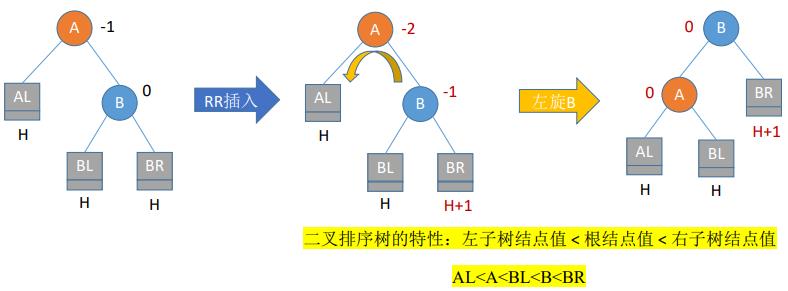
（二）调整最小不平衡子树（RR）

• （2）RR平衡旋转（左单旋转）。由于在结点A的右孩子（R）的右子树（R）上插入了新结点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，而B的原左子树则作为A结点的右子树。
  

（三）代码思路分析

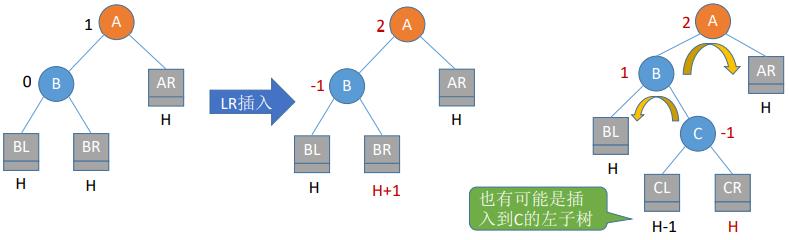
（四）调整最小不平衡子树（LR）

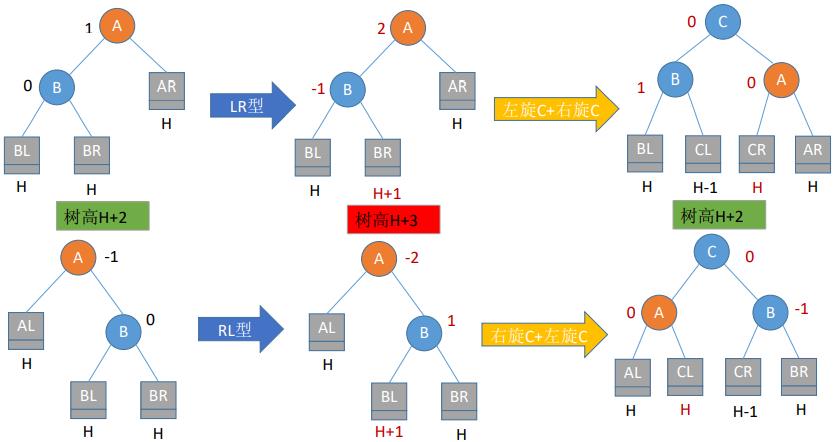
• （3）LR平衡旋转（先左后右双旋转）。由于在A的左孩子（L）的右子树（R）上插入新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后再把该C结点向右上旋转提升到A结点的位置
  
  
  

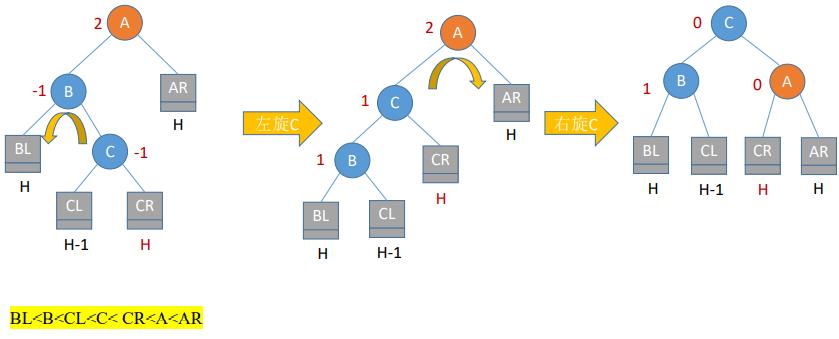
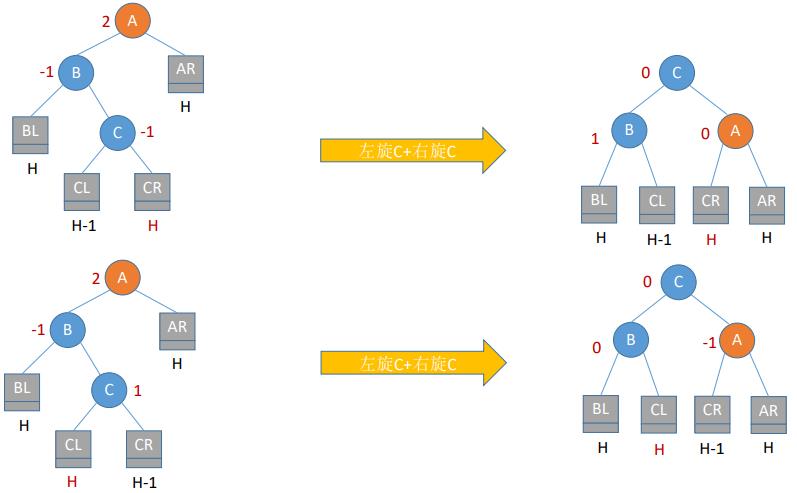
（五）调整最小不平衡子树（RL）

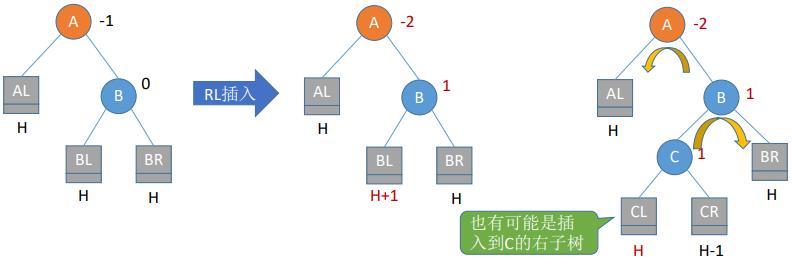
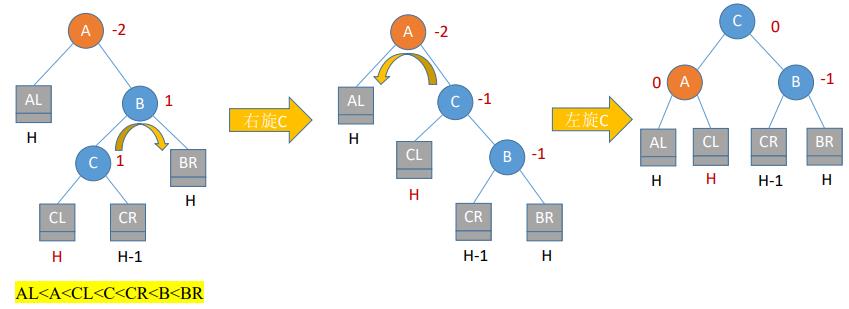
• （4）RL平衡旋转（先右后左双旋转）。由于在A的右孩子（R）的左子树（L）上插入新结点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后再把该C结点向左上旋转提升到A结点的位置
  
  
  

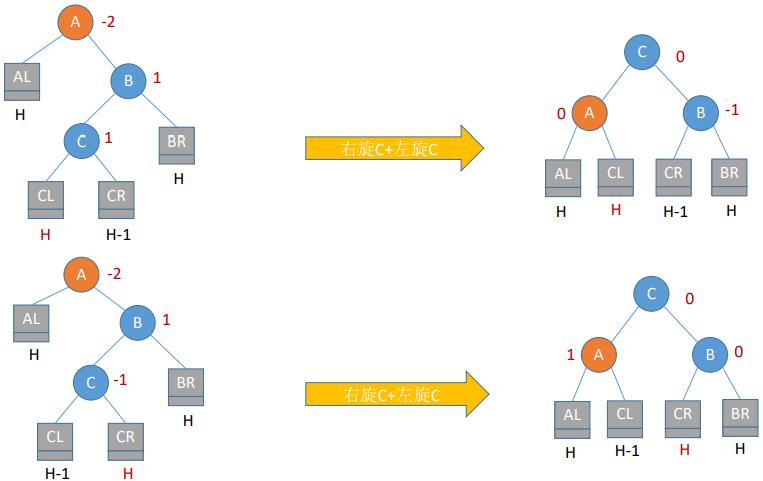
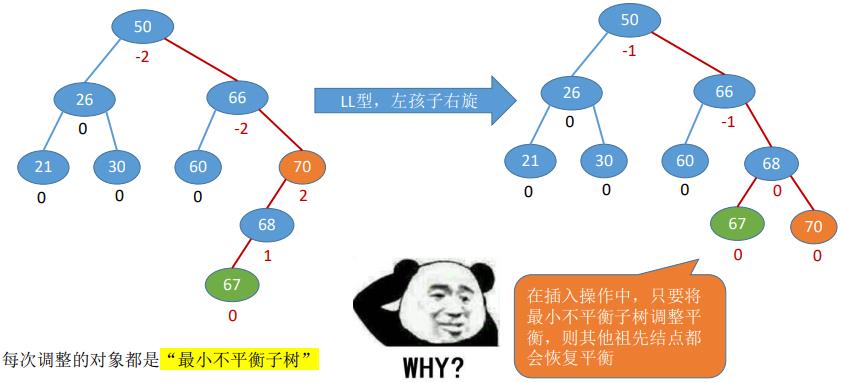
（六）调整最小不平衡子树

每次调整的对象都是“最小不平衡子树”

（七）查找效率分析

• 若树高为h，则最坏情况下，查找一个关键字最多需要对比 h 次，即查找操作的时间复杂度不可能超过 O(h)