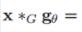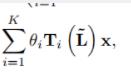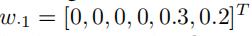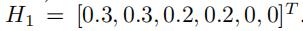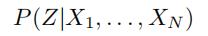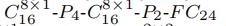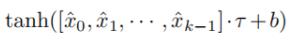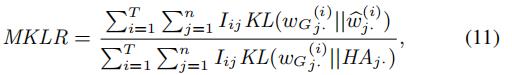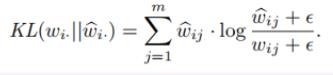论文笔记:Stochastic Weight Completion for Road Networks using Graph Convolutional Networks
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文笔记:Stochastic Weight Completion for Road Networks using Graph Convolutional Networks相关的知识,希望对你有一定的参考价值。
ICDE2019
0 摘要
按需出行服务和无人驾驶都需要高精度的路线规划,这要求对当前路网有一个很精确的表示。
交通网络中的一个子路段的通行时间通常被建模成一个随着时间变化的分布。这个分布可以捕捉不同时间交通的变化情况,以及可以反应“不同的司机可能在同一时间在同一条子路段上的行驶时间不同”的情况。
这样的一个随机权重可以从GPS或者其他检测数据中提取得到。
然而,即使非常庞大的数据也不可能在所有时候都能覆盖所有的子路段。但是高精度路线规划又需要对所有子路段的随机权重。
本篇论文解决了填充确实权重的问题。
本文提出了一种技术,可以通过只覆盖了一部分子路段信息的交通数据,预测所有子路段的随机边权重。
本文提出了一种通用学习框架(图卷积权重补全 graph convolutional weight completion GCWC),该模型可以利用交通路网图的拓扑结构,以及邻接边之间的关联权重,来预测所有边的随机权重。
然后,本文将文本信息融入GCWC中,来进一步提升精准程度。
1 introduction
以出租车为例:
如果出租车考虑不同路径的行驶速度分布而不是平均速度的话,他可能会找到有最高概率准时到达的路径。而是用平均速度的话,可能会导致不可靠的路径选择。
举一个例子:比如我们现在有两条候选路径P1和P2
P1的行驶时间分布为{(30,0.2},(40,0.8)}
P2的行驶时间分布为{(30,0.5),(40,0.3),(50,0.2)}
如果乘客需要在40分钟以内到达机场,那么使用路径P1会比P2好(因为准时到的概率更高)
相反地,如果考虑平均时间的话,P2会更好,因为P2的通行时间期望为37分钟,P1为38分钟。
然而,这样的情况面临数据稀疏性问题(data sparseness problem)。因为交通数据可能并不能覆盖到每一条边上,同时测出来的数据在一些时候可能会出错。
在这篇论文中,我们确定了随机权重补全(stochastic weight completion)问题。给定交通数据,其中只有一部分子路段有数据,我们的目标是将所有的子路段和对应的随机权重一一准确对应。
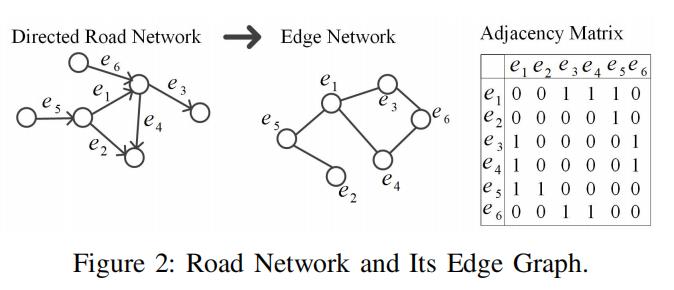
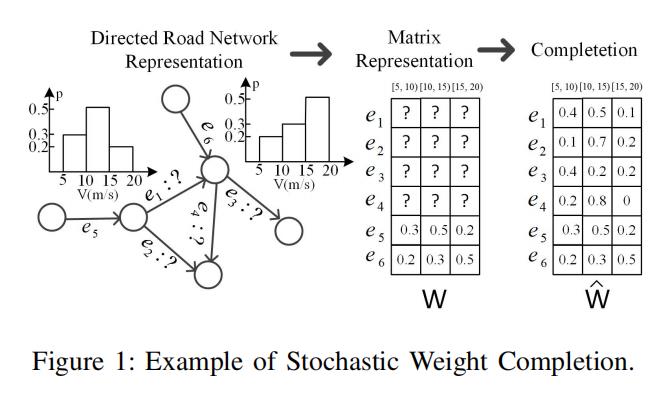
以下图为例:
整个路网中有6条有向边。
我们假设在8:15~8:30的时间段内,只有边e5和边e6有GPS交通数据,并且只有这两个点可以在这个时间段内和随即权重相关联。
比如,当我们在8:15~8:30的时间段内遍历e5,我们有0.3的概率以5m/s~10m/s的速度遍历;有0.5的概率以10~15m/s的速度遍历,有0.2的概率以15~20m/s的速度遍历。
其他边的随机权重(e1,e2,e3,e4)是未知的。可能在其他的时间间隔内,会有另外的一些子路段有数据,但也会有另外的一些子路段没有数据。
为了方便操作,我们将交通图上的这些信息用矩阵的形式表示,其中矩阵的每一行表示了一个子路段的随机权重。(如图1中间部分所示,W的前4行数据是不知道的,因为e1~e4的随机权重数据是未知的。第五行和第六行分别代表了边e5和边e6的随机权重 )
我们随机权重补全的目标是要去预测所有没有交通数据的子路段的随机权重(比如上图的e1~e4)
交通路网中不同边之间的交通速度具有高度的关联性。
之前解决交通数据稀疏性问题(data sparseness)的研究通常假定相邻的边有相似的(基于速度的)权重。
因此,被交通数据覆盖的边的权重可以传播到它们未被交通数据覆盖的相邻边,使用回归与设计过的损失函数,考虑相邻边之间权重的差异。
然而,相似性假设可能并不总是正确的,因为不同边的行进速度之间的相关性可能非常复杂。 仅考虑相邻边之间的权重相似性无法准确地对复杂的相关性进行建模。
此外,现有研究仅考虑确定性权重(例如,平均行驶速度)。 将它们扩展到支持随机权重(例如行驶速度分布)并非易事。
因此,一种能够捕获复杂相关性并支持随机权重的数据驱动方法是亟需的。
我们提出了一个数据驱动的、基于深度学习的框架,其目标是捕获道路网络中边权重之间的复杂相关性,这反过来有助于我们估计没有数据的边的随机权重。
我们首先使用谱图卷积将道路网络的拓扑结构编码为图卷积神经网络 (GCNN)。
然后,我们将可用的交通数据作为输入和有标记的输出,输入到 GCNN模型中,让 GCNN 以“无监督”的方式学习边权重的复杂相关性(即不需要额外的标记数据作为输出)。
然后使用学习的 GCNN 来完成没有数据的边缘的随机权重。
此外,我们提出了一种高级模型,该模型将额外的上下文信息(例如时间间隔、星期几等)作为输入,从而能够进一步提高完成权重的准确性。
我们所提出的框架是通用的,因为它能够支持随机和确定性边缘权重,并且在完成确定性边缘权重时也优于最先进的方法。
据我们所知,这是对随机权重补全的首次研究。
特别是,我们做出了四项贡献:
- 首先,我们将随机权重补全问题形式化。
- 其次,我们提出了一个使用图卷积神经网络的数据驱动框架来解决这个问题。
- 第三,我们通过考虑额外的上下文信息来扩展框架,这进一步提高了准确性。
- 第四,我们使用 GPS 和环路检测器数据集进行了广泛的实验,以深入了解框架的有效性。
2 相关工作
2.1 道路网络中的数据稀缺性问题
尽管交通预测问题已被广泛研究,但只有少数研究考虑了道路网络中的数据稀疏问题。
最近,一种潜在空间模型 (LSM)被提出, 来估计没有环路检测数据的边的权重。在这种模型框架下,该研究使用非负矩阵分解作为编码器来学习潜在空间特征,这有助于在没有数据的情况下估计边的权重。 LSM 是目前最先进的方法。
所有现有的解决数据稀疏问题的研究都只考虑确定性权重,这些方法都不能以直接的方式扩展到随机权重的计算上。
此外,它们都采用线性模型来处理边缘权重之间的相关性。 然而,这种相关性可能是高度非线性的 。
我们提出了一个图卷积权重完成框架,该框架在考虑非线性权重相关性的同时,可以对边的随机权重进行一定的注释。
2.2 交通领域的深度学习问题
基于交通传感器数据,带有自动编码器的 RNN 被用来进行交通预测。
然而,上面这种方法忽略了传感器之间的空间相关性。为了解决这个问题,另一种方法使用扩散卷积网络,它能够对空间相关性进行建模,与 RNN 一起,来进行交通流量预测 。
经典的卷积网络也可以对交通传感器之间的相关性进行建模。但是,这些方法仅限于预测确定性交通流量值,不支持随机值。此外,这些方法假设有足够的交通数据,可以覆盖道路网络中的所有边,而我们的模型则需要考虑数据稀疏的情况。最
近的一项研究侧重于使用多任务学习(multi-task)对起点-目的地对的通行时间进行估计,而不是对交通路段的通行时间进行估计。
多任务学习也用于区分来自不同类型的驾驶员的轨迹[22]。
据我们所知,本文提出的框架是第一个用于道路网络图中随机权重补全的深度学习框架。
3 问题设定
3.1 路网
路网经常被表示成H=(V,E)的形式,其中集合V表示了路口点,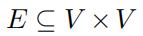 表示了子路段。
表示了子路段。
我们把路网建模成一个图G=(E,A),其中E是边集,A是一个|E|×|E|的邻接矩阵( 表示点i和点j之间有相连边,
表示点i和点j之间有相连边,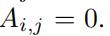 表示点i和点j之间没有相连边)
表示点i和点j之间没有相连边)
下图表示了路网,路网对应的图,以及图的邻接矩阵
3.2 随机权重
为了捕获交通中的时间相关性,我们将一天划分成多个时间片段(eg,将一天分为96个15分钟为间隔的时间片段)。
基于这个,我们可以引入一个随机权重方程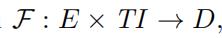 其中TI是整个时间域,E是边集合,D是所有可能的速度分布的集合。
其中TI是整个时间域,E是边集合,D是所有可能的速度分布的集合。
给定一条特定的边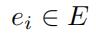 ,以及时间间隔
,以及时间间隔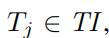 函数
函数 表示在特定的时间间隔TI内,边ei的速度分布
表示在特定的时间间隔TI内,边ei的速度分布
我们首先需要指定我们需要的时间段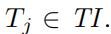
然后我们把边集分成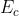 和
和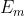 ,这两个集合分别代表了有交通数据和没有交通数据的边集。其中
,这两个集合分别代表了有交通数据和没有交通数据的边集。其中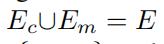
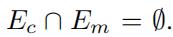
以图1为例, 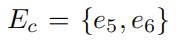
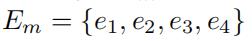 Tj=[8:15,8:30]
Tj=[8:15,8:30]
对于不同的点,直方图的每个柱体代表的间隔是一样的,因此,我们可以用落在不同直方图柱体的概率来表示这条边在特定时间的速度分布。
假设我们有n条边,直方图一共有m个柱体,那么在时间片段Tj,所有边的随机权重可以被表示成一个n×m的矩阵。其中每一行代表了一条边的随机权重(如果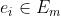 , 那么wi为空)
, 那么wi为空)
3.3 问题格式化
给定一条中某一个时间片段Tj,给定一个初始化的随机权重矩阵W,随机权重补全任务是要把W中的空行填充,赋上我们预测的随机权重,使得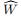 没有空行
没有空行
这相当于对每一个 ,初始化
,初始化
为了方便之后的表述,我们这里形式化一些符号:
| G | 路网图 |
| E | 边集合 |
| V | 点集合 |
| A | 邻接矩阵 |
| n | 边的数量 |
| m | 直方图的W |
| W | 输入的随机权重矩阵 |
 | 实际的随机权重矩阵 |
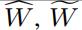 | 预测的和完成的随机权重矩阵 |
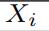 | 文本变量 |
3.4 方法概述
我们提出了一种基本的模型和一种提高版的模型。
基本的模型将一个初始化的、只有一部分行有值的随机权重矩阵W,和边邻接矩阵A作为输入。基本模型的目的是从W和A中学习图卷积核,然后生成一个完整的随机权重矩阵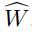
然而,基本模型并没有充分利用很重要的文本信息(contextual information)【比如,不同的时间片段、今天是一个礼拜的星期几)。为了更好地利用这种在基本模型中缺省的信息,我们提出了提高版的模型。
这个模型不仅把W和A作为输入,还把一些文本信息放入输入中,使用贝叶斯推断模型来建立文本信息和基本模型输出之间的关系。这种方式可以提高输出的 随机权重矩阵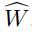 的预测精准度。
的预测精准度。
4 基本模型
4.1 模型概述
不同边之间的随机权重可以共享相关的特征。为了建模这一相关特征,我们将随机权重矩阵W转换成隐藏向量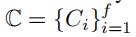 。基于C,我们建立一个没有空行的新随机权重矩阵
。基于C,我们建立一个没有空行的新随机权重矩阵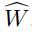
整个过程可以看作一个自动编码器,我们先把不完整的随机权重矩阵编码成C,然后将C解码成完整的权重编码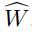
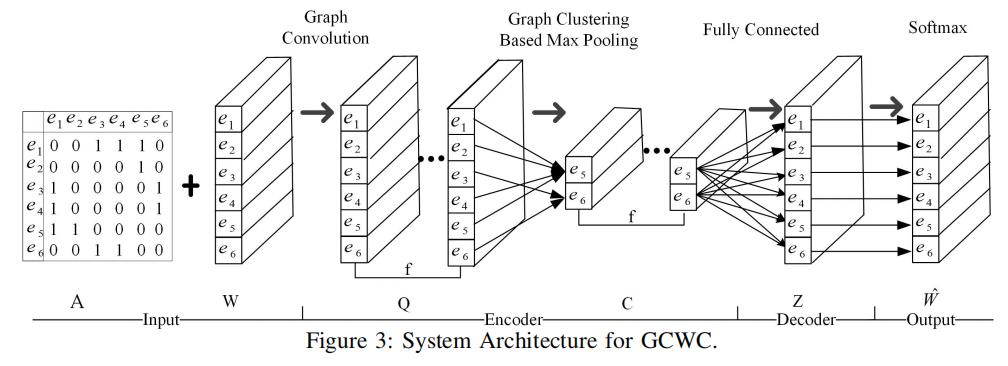
上图展示了GCWC的完整架构
首先,我们把随机权重矩阵W以及邻接矩阵A作为输入,喂入GCWC中
然后,我们使用卷积和最大池化将W编码成一组特征是C的向量
之后,我们分别通过全连接层和softmax层(最终输出层)编码C,并得到最终估计得到的 随机权重矩阵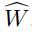 (类似于自动编码器中的解码操作)
(类似于自动编码器中的解码操作)
在训练阶段,W也会在反向传播阶段被用作标签(label)的来源。我们可以通过最小化损失函数的方式来学习框架的参数,其中损失函数被定义为:我们估计的随机权重矩阵和实际的随机权重矩阵之间(有交通数值的初始化随机权重)的KL散度
4.2 卷积层
在传统的CNN中,基于“输入矩阵相邻的元素共享相似的特征”这一假设,二维的卷积核被CNN模型使用。

但在我们的设置中,作为输入的随机权重矩阵可能不能很好地满足这一假设(比如还是图1中,e5和e6在随机权重矩阵上是相连的,但是在交通图上是不相连的)。
因此,我们使用了GCN来将路网的拓扑结构考虑进我们的模型中。这里我们使用简化的切比雪夫GNN(Simplified ChebNet)
4.2.1 ChebNet
我们记拉普拉斯矩阵为L=D-A,标准化拉普拉斯矩阵为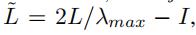 ,其中
,其中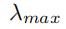 是L最大的特征值
是L最大的特征值
在卷积层中,我们通过使用标准化拉普拉斯矩阵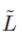 ,把图卷积核使用到输入的随机权重矩阵W上。
,把图卷积核使用到输入的随机权重矩阵W上。
W矩阵的列向量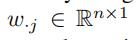 表示了所有节点在第j个数据区间的权重(概率)大小,(j∈[1,m])
表示了所有节点在第j个数据区间的权重(概率)大小,(j∈[1,m])
基于某一个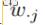 和
和 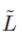 ,我们可以生成一个矩阵
,我们可以生成一个矩阵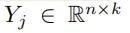 ,其中
,其中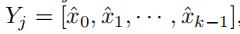 。这里
。这里 表示x和第i阶切比雪夫多项式卷积核的卷积结果(即
表示x和第i阶切比雪夫多项式卷积核的卷积结果(即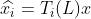 ),k是一个超参数,表示切比雪夫多项式进行到几阶。
),k是一个超参数,表示切比雪夫多项式进行到几阶。
图卷积为
详细地来说,首先 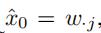 然后
然后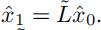 (
(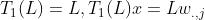 )
)
然后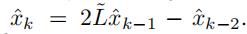
最后我们定义了一个过滤器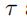 (
(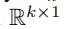 维度的矩阵),来将各个xi加权求和
维度的矩阵),来将各个xi加权求和
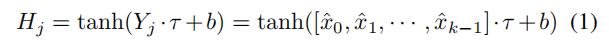
这时候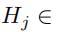
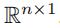
还是以图1为例,图1有6条边和3个不同的速度区间。对于[5,10)的速度区间,我们有:
假设k=2,那么我们通过邻接矩阵A来构建相应的Y1:
第一行就是
,第二行是
和加权的拉普拉斯矩阵相乘之后的结果
然后,我们将
作为过滤器,和Y1相乘,得到加权后的H1:
求得H1之后,边e5和边e6的信息就被传递到边e1,e2,e3,e4中去了
给定一个作为输入的随机权重矩阵W,对于W中的每一个列向量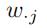 (j∈[1,m]),我们将f个过滤器
(j∈[1,m]),我们将f个过滤器 应用到他们的切比雪夫简化GNN中。
应用到他们的切比雪夫简化GNN中。
于是,对每一个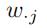 ,我们得到f个相应的H:
,我们得到f个相应的H: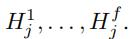 ‘
‘
然后,对于每一个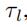 ,(l∈[1,f]),我们将所有列向量
,(l∈[1,f]),我们将所有列向量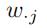 求得的H(卷积结果)求和(求和结果Ql是一个
求得的H(卷积结果)求和(求和结果Ql是一个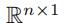 向量)
向量)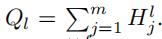
接着,我们把所有的Q叠加起来,得到一个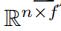 矩阵
矩阵 这个Q就是最终从卷积层得到的结果。(f个过滤器代表了f个不同特征)
这个Q就是最终从卷积层得到的结果。(f个过滤器代表了f个不同特征)
4.3 池化层
在卷积层中,有些边可能仍然只有零值。因此我们进一步通过最大池化操作(max pooling)压缩卷积结果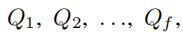
我们使用一个基于图的多层池化算法,使用图的拓扑结构和随机权重分布,来识别边之间的集簇关系。
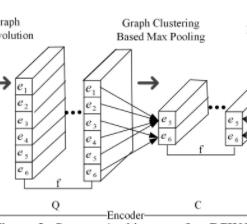
比如,在图3中,e1,e2,e4,e5汇成一个集簇,e3,e6汇成另外的一个集簇
基于这个分集簇的方法,每一个卷积矩阵Ql被进一步压缩成更紧缩的矩阵Cl(l∈[1,f]),现在,我们把这一组Ci的值看成隐空间上的特征集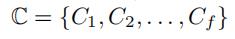
4.4 输出层
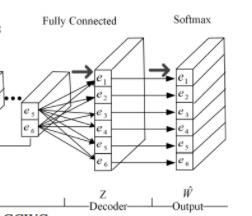
经过池化层之后,我们获得了可以捕获输入矩阵W特征的压缩矩阵C。于是,我们可以将压缩矩阵解码成一个新的随机权重矩阵
我们首先使用一个全连接层来获得一个矩阵Z,这个矩阵代表了从集合C中解码得到的所有边的随机权重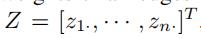 (其中n是边的数量,
(其中n是边的数量, 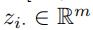 ,m是速度区间的数量)
,m是速度区间的数量)
4.4.1 softmax层
但是最终的输出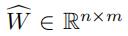 需要满足两个条件
需要满足两个条件
1,对于每一个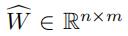 中的
中的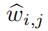 (i∈[1,n],j∈[1,m]),它的取值都必须在[0,1]之间
(i∈[1,n],j∈[1,m]),它的取值都必须在[0,1]之间
2,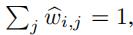
于是,我们对每一个 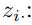 使用softmax:
使用softmax:
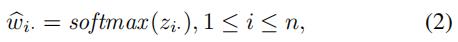
最终,我们有: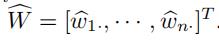
4.5 损失函数
GCWC的损失函数 使用了KL散度衡量输入随机权重矩阵
使用了KL散度衡量输入随机权重矩阵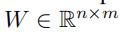 和预测随机权重矩阵
和预测随机权重矩阵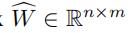 之间的差距:
之间的差距:

我们一共有n条边,但是模型重点是有观测数据的那一些边。因此我们在损失函数那里设置了一个权重函数I,当第i条边有观测交通数据的时候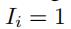 ,否则
,否则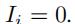
这里我们使用ε是为了防止log的时候出现0
5 带文本的GCWC
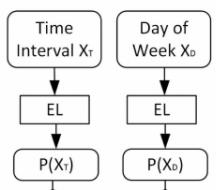
当我们考虑某一特定时间片段的随机权重矩阵W的时候,我们可以同时考虑一组文本信息。
在这里,我们考虑三种文本信息:时间片段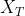 ,周中星期几
,周中星期几 以及是否有观测值
以及是否有观测值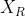
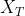 :我们使用一个one-hot向量来表示一天中特定的时间片段(比如,如果我们要描述[0:15,0:30],那么就是第二个维度为1,其他的都是0)
:我们使用一个one-hot向量来表示一天中特定的时间片段(比如,如果我们要描述[0:15,0:30],那么就是第二个维度为1,其他的都是0)
 :我们使用一个7位的one-hot向量来表示这是星期几
:我们使用一个7位的one-hot向量来表示这是星期几
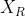 :表示在当前时间片段内,哪些边有观测数值(
:表示在当前时间片段内,哪些边有观测数值(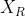 是一个n维向量,哪一条边有值,那么对应的维度为1,否则为0)
是一个n维向量,哪一条边有值,那么对应的维度为1,否则为0)
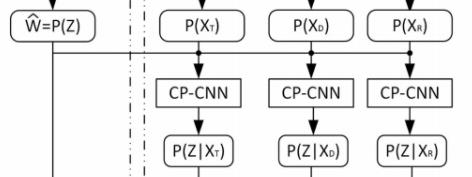
下图是带文本的GCWC的流程图:
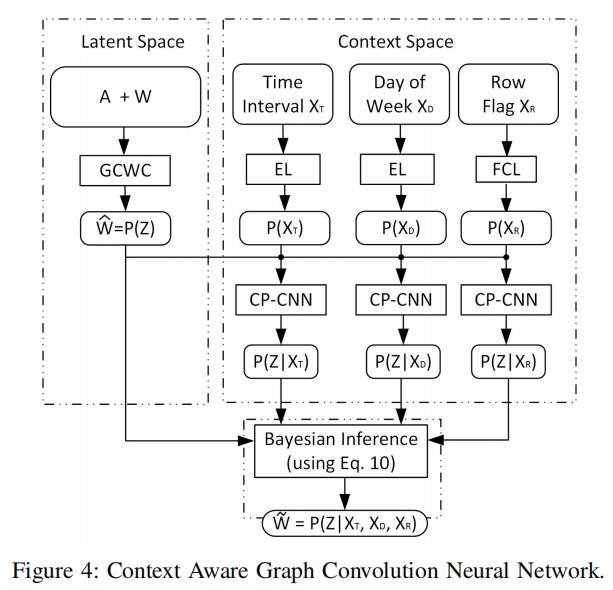
我们这里使用P(Z)表示基本GCWC的输出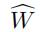 ,其中P()表示softmax操作
,其中P()表示softmax操作
文本嵌入模块首先把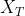 、
、 、
、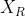 表示成相同维度的向量。然后和GCWC的输出P(Z)一起,分别求得有了各个文本之后,有预测的随机权重矩阵Z的条件概率
表示成相同维度的向量。然后和GCWC的输出P(Z)一起,分别求得有了各个文本之后,有预测的随机权重矩阵Z的条件概率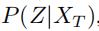 、
、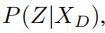 、
、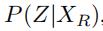
贝叶斯推断模块将P(Z)、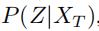 、
、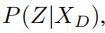 、
、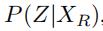 作为输入,他求得有了所有文本信息之后,有Z的概率
作为输入,他求得有了所有文本信息之后,有Z的概率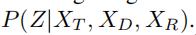
5.1 文本嵌入模块
这里的文本嵌入模块具有一定的普适性——也就是说,不止我们之前说的三种文本信息适用,之后如果我们还有其他的文本信息(天气情况,交通状况,等等),一样可以使用这个文本嵌入模块。
鉴于不同的 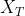 、
、 、
、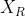 ,我们使用了两种不同的模型(嵌入模型和全连接模型)
,我们使用了两种不同的模型(嵌入模型和全连接模型)
5.1.1 嵌入层(embedding layer)
对于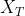 、
、 ,我们使用了嵌入层,将one-hot 稀疏编码 表示成更 紧致的向量。
,我们使用了嵌入层,将one-hot 稀疏编码 表示成更 紧致的向量。
对于某一个one-hot 向量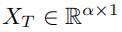 ,嵌入层的作用是将
,嵌入层的作用是将 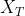 表示成
表示成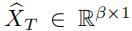 (其中
(其中 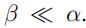 )
)
然后,我们对每一个学到的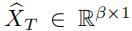 使用softmax函数,得到
使用softmax函数,得到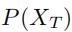
相似地,我们可以得到
5.1.2 全连接层
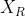 中可能不止一个1.而在一些embedding方法中,输入的向量必须是one-hot 向量。于是,我们引入了一种全连接层来将
中可能不止一个1.而在一些embedding方法中,输入的向量必须是one-hot 向量。于是,我们引入了一种全连接层来将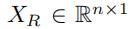 嵌入到更低维的空间中
嵌入到更低维的空间中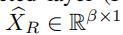 (其中,
(其中,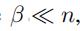 )
)
用公式表示,我们有
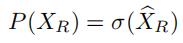
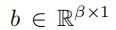
这里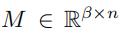 是权重矩阵,
是权重矩阵,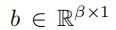 是偏差向量,σ是softmax函数
是偏差向量,σ是softmax函数
5.2 计算条件概率
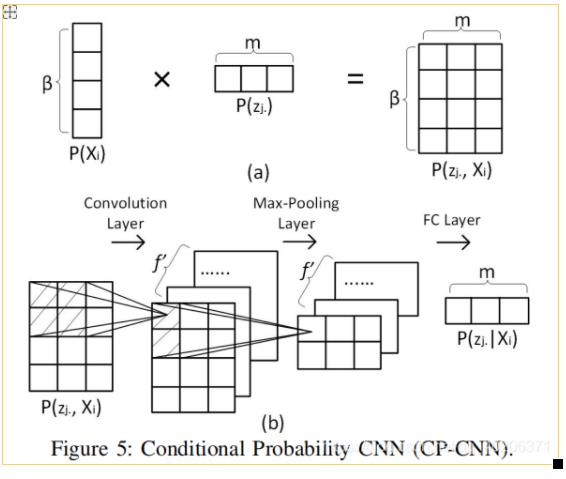
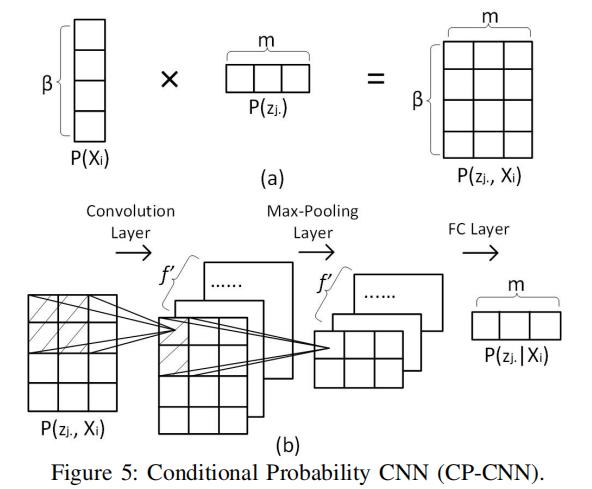
我们使用了条件概率卷积神经网络(conditional probability convolutional neural network CP-CNN)来捕获边j的随机权重zj和不同类型的文本之间的关系
为了简化说明,我们用Xi表示文本。(Xi可以是 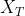 、
、 、
、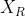 )
)
如上图5(a)所述,我们将 和
和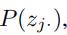 相乘。
相乘。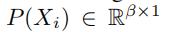 是之前用嵌入层或者全连接层得到的文本表示。
是之前用嵌入层或者全连接层得到的文本表示。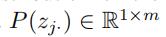 是前面GCWC得到的某一条特定的边对应的随机权重。
是前面GCWC得到的某一条特定的边对应的随机权重。
作为结果,我们得到了 一个矩阵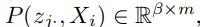 ,该矩阵将第j条边的随机权重和不同文本信息联系了起来。
,该矩阵将第j条边的随机权重和不同文本信息联系了起来。

然后我们使用经典的卷积过滤来捕获随机权重在各个文本下的条件概率。

还是以图1为例,我们有3段速度区间[5,10),[10,15),[15,20) 【注:原文是[0,20),[20,40),[40,60),感觉是不是原文写错了】。如果我们使用2*2的卷积核在图5(b)的最左边阴影区间内,我们将可以捕获两个速度区间和两个文本条目之间的关系(比如,速度 [5,10),[10,15)和时间片段[8:00,8:15],[8:15,8:30])
如图5(b)所示,我们使用f'个卷积核,得到了f’个矩阵,每个矩阵的大小为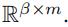
接着,我们使用一个大小为2的最大池化层来学习更多的关联性 。通过池化层之后,我们将获得大小为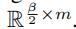 的矩阵
的矩阵
然后我们使用全连接层将f'个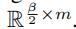 的矩阵拼接成一个
的矩阵拼接成一个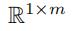 的向量,这个向量
的向量,这个向量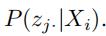 便代表了j边的随机权重在已知文本Xi下的条件概率。
便代表了j边的随机权重在已知文本Xi下的条件概率。
以此类推,我们可以对所有的n条边进行以上操作,得到 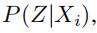 即当我们得到文本信息Xi时候的随机权重矩阵
即当我们得到文本信息Xi时候的随机权重矩阵

5.3 贝叶斯推断
我们使用贝叶斯推断模型来获得一个已知所有类型的文本信息 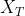 、
、 、
、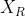 的情况下,随机权重矩阵Z的条件概率
的情况下,随机权重矩阵Z的条件概率
一般地,假设我们有N种类型的文本信息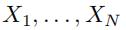 ,我们通过上一步获得了Z在各个条件下分别的条件概率
,我们通过上一步获得了Z在各个条件下分别的条件概率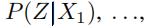
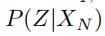 。我们现在要做的是求得
。我们现在要做的是求得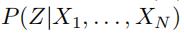 ,作为我们最终的随机权重矩阵。
,作为我们最终的随机权重矩阵。
在这里,我们假设不同的文本信息之间是独立的,即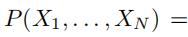
 ,这个也是很直观的,类似于一天中的时间、一周中的星期几、那几个路段有数据等,都是独立的,没有很明显的相关性。
,这个也是很直观的,类似于一天中的时间、一周中的星期几、那几个路段有数据等,都是独立的,没有很明显的相关性。
于是,我们有:
(贝叶斯定理)
(我们假设的独立性)
(条件概率)
(X1,...XN独立,自然也在Z下条件独立)
(分子分母同时乘以N-1个P(Z))
(分母条件概率合并,分子提上去)
(条件概率)
因此,我们可以计算我们的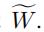 =
=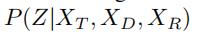

然后,我们需要对(10)的结果进行正则化,使得
1)对于每一个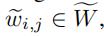

2)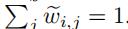
5.4 损失函数
这里的损失函数和之前GCWC的一致,我就把之间的内容贴过来了
GCWC的损失函数
使用了KL散度衡量输入随机权重矩阵
和预测随机权重矩阵
之间的差距:
我们一共有n条边,但是模型重点是有观测数据的那一些边。因此我们在损失函数那里设置了一个权重函数I,当第i条边有观测交通数据的时候
,否则
这里我们使用ε是为了防止log的时候出现0
6 实验部分
6.1 数据集
我们使用两个交通的数据集。同时,我们将速度片段从0到40m/s八等分。
6.1.1 HW(highway tollgate network)
这个数据集有24个子路段,因此我们的随机权重矩阵为: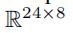
6.1.2 CI (city road network)
这个数据集是从14864辆成都的出租车上获得的。我们使用其中的172个子路段,因此这个数据集的随机权重矩阵为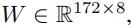
6.1.3 ground truth 和输入数据
给定了时间片段之后,我们就可以构建ground truth的随机权重矩阵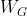 ,我们只建立至少有5段观测记录的边。
,我们只建立至少有5段观测记录的边。
然后我们从n条边中随机选择 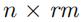 条边(rm是一个移除比例,在这里我们设置为0.5,0.6,0.7,0.8),将这些边的随机权重设置为0。于是我们得到了我们的输入W。将W作为输入,我们就可以用我们之前介绍的模型来估计一个随机权重矩阵
条边(rm是一个移除比例,在这里我们设置为0.5,0.6,0.7,0.8),将这些边的随机权重设置为0。于是我们得到了我们的输入W。将W作为输入,我们就可以用我们之前介绍的模型来估计一个随机权重矩阵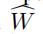 。我们可以通过比较
。我们可以通过比较 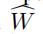 和
和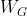 之间的差距来判断我们模型的精准程度。
之间的差距来判断我们模型的精准程度。
需要注意的是,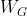 可能本来就有空行(鉴于某一些边可能本来就没有交通观测值,或者交通观测值小于5个,我们不初始化这条边)。尽管如此,我们还是需要将一些边的随机权重抹除(这样才能够训练,知道我们参数的选择正确与否)
可能本来就有空行(鉴于某一些边可能本来就没有交通观测值,或者交通观测值小于5个,我们不初始化这条边)。尽管如此,我们还是需要将一些边的随机权重抹除(这样才能够训练,知道我们参数的选择正确与否)
对于数据集,我们将数据集分成五份,使用5折交叉验证(5-cross validation)来进行训练。
6.2 模型的功能
我们提出的两个模型,GCWC和A-GCWC都是具有一定普适性的。我们把模型的设定稍作修改,便可以得到不同的功能。
这里,我们考虑三种功能:估计/预测随机权重矩阵(以直方图的形式),估计平均速度(以确定值的形式)。这里我们用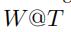 来表示时间片段T下的权重矩阵。
来表示时间片段T下的权重矩阵。
6.2.1 估计 estimation
给定Ti时刻的输入随机权重矩阵 (其中有一些边没有权重),我们去预测
(其中有一些边没有权重),我们去预测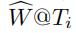
在训练的时候,对于训练集 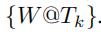 (不同时刻的输入随机权重矩阵),我们使用
(不同时刻的输入随机权重矩阵),我们使用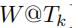 自己作为标签,来训练GCWC和A-GCWC。
自己作为标签,来训练GCWC和A-GCWC。
在测试的时候,给定输入随机权重矩阵 ,估计的随机权重矩阵
,估计的随机权重矩阵 会和ground truth随机权重矩阵
会和ground truth随机权重矩阵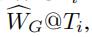 相比较
相比较
6.2.2 预测prediction
给定Ti时刻的输入随机权重矩阵 (其中有一些边没有权重),我们去预测
(其中有一些边没有权重),我们去预测
训练的时候,对于训练集 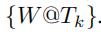 (不同时刻的输入随机权重矩阵),我们使用
(不同时刻的输入随机权重矩阵),我们使用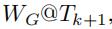 作为标签,来训练GCWC和A-GCWC。
作为标签,来训练GCWC和A-GCWC。
与此同时,我们要确认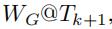 和
和 有相同的移除比例rm
有相同的移除比例rm
在测试的时候,给定输入随即权重 ,预测的随机权重矩阵
,预测的随机权重矩阵 会和ground truth 随机权重矩阵
会和ground truth 随机权重矩阵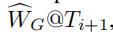 相比较
相比较
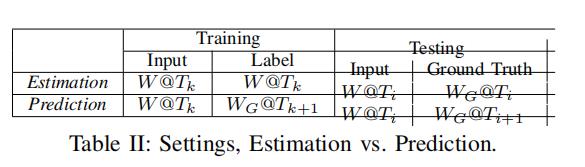
表2说明了estimation和prediction之间的异同
6.2.3 平均 average
这个的配置和估计estimation类似,给定输入矩阵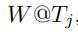 ,我们希望在时间片段Tj时预估每一条边的确定平均速度
,我们希望在时间片段Tj时预估每一条边的确定平均速度
之后这一部分我持保留意见,原文的意思是把4.4 公式(2)中的softmax替换成sigmoid;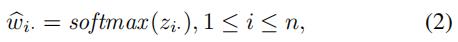 ,就能得到一个
,就能得到一个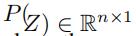 ,但是sigmoid如果参数是一个向量的话,结果应该还是一个向量才对,维度应该不会变成1维的(softmax然后加权求和我觉得就可以了,这个我事后看一下作者的code,想一想是不是我理解错了,这里放一个伏笔)
,但是sigmoid如果参数是一个向量的话,结果应该还是一个向量才对,维度应该不会变成1维的(softmax然后加权求和我觉得就可以了,这个我事后看一下作者的code,想一想是不是我理解错了,这里放一个伏笔)
6.3 模型的设定
在表3中,我们展现了所有模型的超参数(注:A-GCWC的β参数,也就是各文本被压缩到的响亮的维度,统一设置为4)
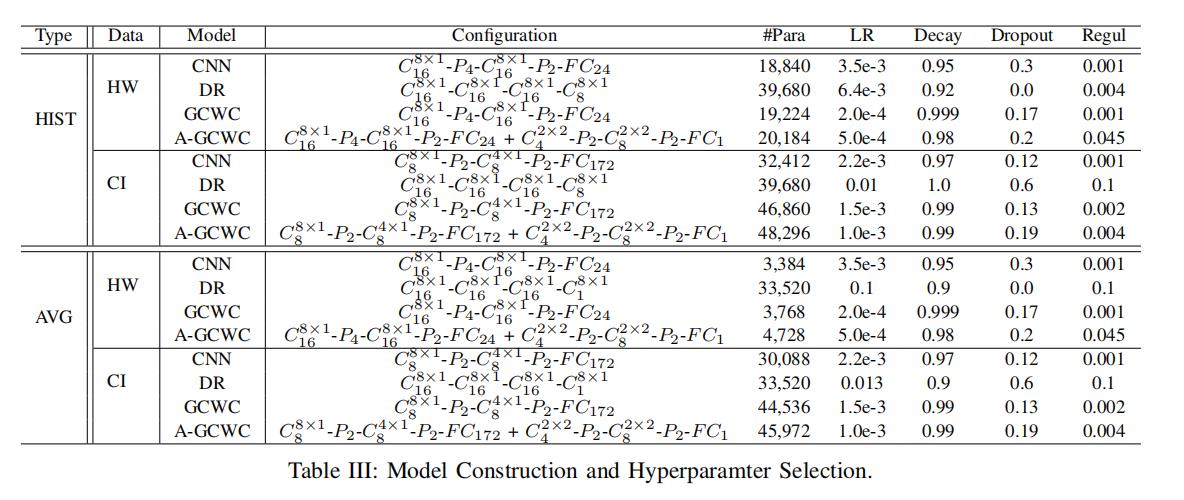
我们将为了估计和预测任务的模型记为HIST,将为了平均任务的模型记为 AVG
在表格中,#Para表示参数的总数(卷积核的参数、全连接层的参数、激活函数的偏差等),这个代表了不同神经网络的复杂度。这个数值越大,表示神经网络越复杂。通过表格中的#Para,我们可以得到结论:CNN、GCWC、A-GCWC使用的参数量差不多,也就是说,相比于传统的CNN ,我们提出的GCWC和A-GCWC模型并没有怎么增加模型的复杂度
LR表示学习率(learning rate),Decay 表示学习率损失,Regul表示 正则化系数(regularization)
我们用以下的表述来描述模型的结构:
 表示卷积层有f个卷积的过滤单元,每一个filter是一个
表示卷积层有f个卷积的过滤单元,每一个filter是一个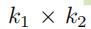 的矩阵
的矩阵
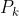 表示了一个大小和跨度都是k的池化层
表示了一个大小和跨度都是k的池化层
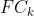 表示了一个有k个隐藏单元的全连接层
表示了一个有k个隐藏单元的全连接层
我们分别以GCWC和A-GCWC的参数为例:
HW的GCWC:
对HW来说,其有24个子段,8个时间片段,
对于
,8表示我们切比雪夫多项式近似的时候,结束选择的是8,也就是下式(在4.2出现过)的k=8:
所以也就相当于
是一个1×8的向量。
16表示我们有16个
没太搞明白,在GCWC中的池化操作是使用图的拓扑结构和随机权重分布,来识别边之间的集簇关系。不知道这边4和2代表的size和stride是什么,和CNN中的池化有何异同(后面看代码之后回来填坑)
表示我们全连接层的输出为24维参数。这里的24是因为HW有24个子路段
HW的A-GCWC:
前半部分和GCWC的分析一致
后半部分是融入context部分的内容。
是图5(b)左边的内容,2×2的filter,一共有4个filter
这里的
指的是图5(b)中间的部分,两块通过max pooling合并成一块的操作
是把这一个速度区间的所有隐藏状态通过全连接的方式合并为一个
6.5 baseline
| HA (historical average) | 一条边上过去时间的通行速度记录的平均值 |
| GP gaussian process | 高斯过程回归模型 |
| RF random forest | 随机森林模型 |
| LSM | 利用潜在空间模型填补道路网络中缺失权重的最新技术。 |
注意:GP\\RF\\LSM只能预测、估计确定值。因此,我们对不同的速度片段下的随机权重,分别学习了一个回归任务。
| CNN | |
| DR diffusion convolutional recurrent neural network | 基于历史数据预测确定性边权的最新技术。 |
6.6 评估方法
6.6.1 估计和预测(estimation & prediction)
我们使用平均KL散度比例(MKLR Mean Kullback-Leibler divergence Ratio)来衡量预测的随机权重矩阵
的精准程度
T是所有时间片段数量的总和
n是边的数量
i∈[1,T],j∈[1,n],表明了在第i个时间片段,边j是否需要被评估
如果边j没有交通观测数据,那么I设置为0;否则I设置为1。
是ground-truth结果。
是预测/估计结果
KL(·||·)表示两个分布的KL散度(前文也有说明),两个分布越相似,KL散度的值越小。
但是KL散度的取值范围是[0,∞),所以我们不太容易判断什么样的KL散度值是足够小的
于是我们用HA(historical average)作为一个参考的随机权重,即baseline。我们认为HA是随机权重最差的预测/估计。然后我们使用我们的模型和HA模型的KL散度的比例,MKLR作为衡量标准。这个比例表明了我们的模型相比于HA提升了多少 。比例越小,表示相比于HA,我们的模型提升得越多
我们也可以使用相似比例(FLR, fraction of likelihood ratio)来衡量预测/估计的精准程度
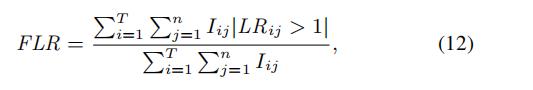
T,n, 的定义和MKLR中的说法是一样的
的定义和MKLR中的说法是一样的
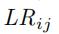 代表了第i个时间片段中,第j条边的相似比例
代表了第i个时间片段中,第j条边的相似比例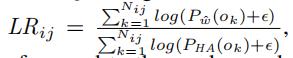
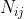 表示在第i个时间片段中,第j条边上ground truth的速度记录数(在一个时间片段中,可能有多条记录)
表示在第i个时间片段中,第j条边上ground truth的速度记录数(在一个时间片段中,可能有多条记录)
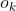 是第k个ground truth的速度纪录
是第k个ground truth的速度纪录
ε用来防止log里的内容是0
我们给定第j条边和第i段预测片段,我们可以有预测/估计的随机矩阵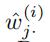 以及作为参考的随机矩阵
以及作为参考的随机矩阵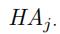 我们分别计算
我们分别计算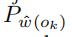
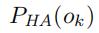 , 作为从这两个随机矩阵代表的分布中,观测到
, 作为从这两个随机矩阵代表的分布中,观测到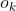 的概率
的概率
如果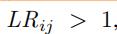 ,那么 表明我们的预测/估计模型有更大的概率得到ground truth 速度纪录,那么我们设置此时的这个
,那么 表明我们的预测/估计模型有更大的概率得到ground truth 速度纪录,那么我们设置此时的这个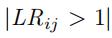 ,否则为0
,否则为0
6.6.2 平均
我们使用MAPE
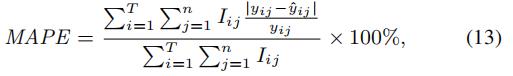
T,n, 的定义和前文中的说法是一样的
的定义和前文中的说法是一样的
6.7 实验结果
6.7.1 估计:MKLR
MKLR越小,精度越高
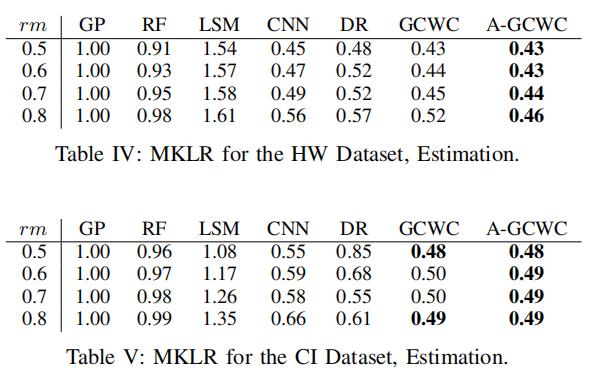
- A-GCWC在各种配置下,都有最好的精确程度,同时A-GCWC模型比GCWC模型更稳定
- 几乎所有的方法都满足:当移除几率rm增加的时候,MKLR增加。 ——原因也很简单,因为rm增加了之后,更少的边有交通观测数据,那么更多的边需要被赋以预测的随机权重
- LSM,目前在权重补全任务中的最新方法,并不能适配我们所考虑的配置,他的所有MKLR都为1,这说明LSM勉强和HA效果差不多——这说明LSM模型不能扩展到随机权重任务,同时LSM不能解决很多边都没有交通数据的情况。
- CNN的MKLR会随着rm增大显著变化,——这是因为CNN不能很好地捕捉路网中的时空关系
- DR在HW数据中的效果比CI好——DR在小图中有很好的传播能力,但是在大图中则不行
6.7.2 估计:FLR
FLR越大,精度越大
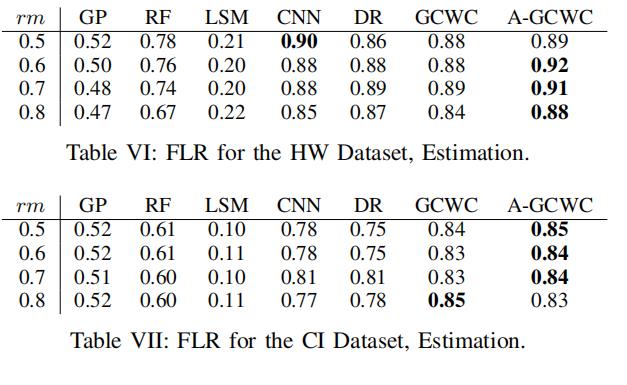
- 和MKLR一样,LSM同样效果不好(大部分时候不如HA)
- 大部分配置下,我们的A-GCWC和GCWC效果最好(A-GCWC的效果比GCWC的效果好)
- CNN在某几个特定的配置下(HW,rm=0.5),效果比我们的模型好(因为在小的路网中,很多边都有数据的情况下,CNN可能也能捕获一些边随机权重的相关系数)
- DR和前面分析的一样,在HW中表现得很好,在CI中表现得很差——DR在小图中有很好的传播能力,但是在大图中则不行
6.7.3 预测:MKLR
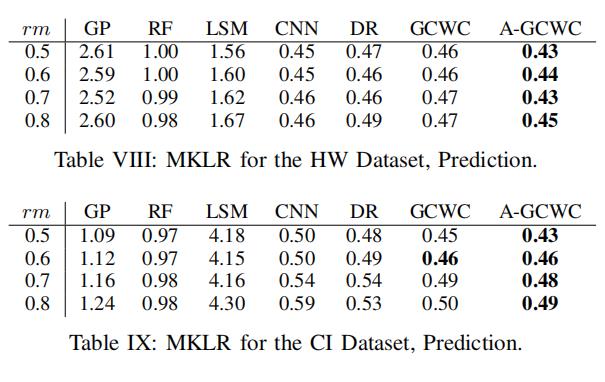
在数据集HW上 ,大部分方法都满足估计(6.7.1)的结论:rm增加,MKLR增加(除了GP和RF)
而在数据集CI上,这样的一个结论就不怎
以上是关于论文笔记:Stochastic Weight Completion for Road Networks using Graph Convolutional Networks的主要内容,如果未能解决你的问题,请参考以下文章
SWA(Stochastic Weight Averaging)实验
论文阅读笔记《Stochastic Grounded Action Transformation for Robot Learning in Simulation》
论文阅读Stochastic Variance Reduced Ensemble Adversarial Attack for Boostingthe Adversarial
机器学习笔记:随机深度网络 stochastic depth