数据结构学习笔记(栈队列)整理与总结
Posted 康x呀
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构学习笔记(栈队列)整理与总结相关的知识,希望对你有一定的参考价值。
数据结构学习笔记(栈、队列)整理与总结
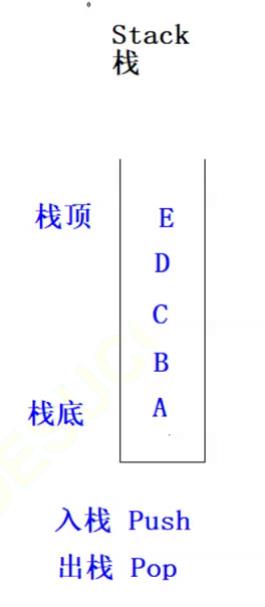
栈
栈的概念:
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
结构:
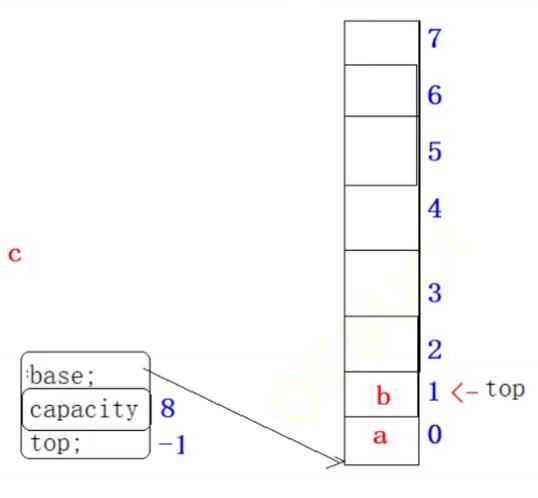
栈结构之顺序栈的基本介绍
概念: 栈是限定仅在表尾进行插人或删除操作的线性表。因此,对栈来说,表尾端有其特殊含义,称为栈顶,相应地,表头端称为栈底。不含元素的空表称为空栈。栈的修改是按后进先出的原则进行的,因此栈又称为后进先出的线性表,简称LIFO结构。而顺序栈就是使用顺序结构来实现栈,顺序栈的空间是连续分配的。
结构图:
结构代码描述:
定义顺序栈结构体:
// An highlighted block
//顺序栈
typedef struct SeqStack
{
ElemType *base; //栈空间
size_t capacity;
size_t top; //栈顶指针
}SeqStack;
顺序栈的常用操作
**初始化顺序栈**
// An highlighted block
void SeqStackInit(SeqStack *pst, int sz)
{
//设置容量的初始化大小
pst->capacity = sz > SEQ_STACK_DEFAULT_SIZE ? sz : SEQ_STACK_DEFAULT_SIZE;
//申请空间
pst->base = (ElemType *)malloc(sizeof(ElemType) * pst->capacity);
assert(pst->base != NULL);
pst->top = 0;//栈顶的初始化指向
}
**判断栈是否满或者空**
// An highlighted block
//判断栈是否满
bool IsFull(SeqStack *pst)
{
return pst->top >= pst->capacity;
}
//判断栈是否空
bool IsEmpty(SeqStack *pst)
{
return pst->top == 0;
}
**入栈**
// An highlighted block
void SeqStackPush(SeqStack *pst, ElemType v)
{
if(IsFull(pst))
{
printf("栈已满,%d不能入栈.\\n", v);
return;
}
pst->base[pst->top++] = v;//放到top所指的下标的空间,然后top再++
}
**出栈**
// An highlighted block
void SeqStackPop(SeqStack *pst)
{
if(IsEmpty(pst))
{
printf("栈已空,不能出栈.\\n");
return;
}
pst->top--;//出栈
}
**获取栈顶元素**
// An highlighted block
ElemType SeqStackTop(SeqStack *pst)
//void SeqStackTop(SeqStack *pst, ElemType *v) //出参
{
if(IsEmpty(pst))
{
printf("栈已空,没有栈顶元素.\\n");
return;
}
return pst->base[pst->top-1];//top-1不会更改top指针的指向,这样就不会删除指向的元素
//*v = pst->base[pst->top-1];
}
**打印栈内所有数据**
// An highlighted block
void SeqStackShow(SeqStack *pst)
{
for(int i=pst->top-1; i>=0; --i)
printf("%d\\n", pst->base[i]);
}
**顺序栈的摧毁**
// An highlighted block
void SeqStackDestroy(SeqStack *pst)
{
free(pst->base);
pst->base = NULL;
pst->capacity = pst->top = 0;
}
栈结构之链栈的基本介绍
概念: 栈是限定仅在表尾进行插人或删除操作的线性表。因此,对栈来说,表尾端有其特殊含义,称为栈顶,相应地,表头端称为栈底。不含元素的空表称为空栈。栈的修改是按后进先出的原则进行的,因此栈又称为后进先出的线性表,简称LIFO结构。而链栈就是使用链式结构来实现栈,链栈的空间可以是不连续分配。
结构:
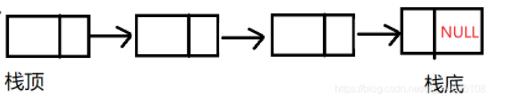
**代码描述:**
// An highlighted block
typedef struct LinkStackNode
{
ElemType data;
struct LinkStackNode *next;
}LinkStackNode;
typedef struct LinkStack
{
LinkStackNode *head;
}LinkStack;
链栈的常用操作
**初始化**
// An highlighted block
void LinkStackInit(LinkStack *pst)
{
pst->head = NULL;
}
**入栈**
// An highlighted block
void LinkStackPush(LinkStack *pst, ElemType v)
{
LinkStackNode *s = (LinkStackNode*)malloc(sizeof(LinkStackNode));
assert(s != NULL);
s->data = v;
s->next = pst->head;
pst->head = s;
}
**出栈**
// An highlighted block
void LinkStackPop(LinkStack *pst)
{
LinkStackNode *p;
if(pst->head == NULL)
return;
p = pst->head;
pst->head = p->next;
free(p);//记得释放,都是malloc出来的
}
**栈顶元素**
// An highlighted block
ElemType LinkStackTop(LinkStack *pst)
{
assert(pst->head != NULL);
return pst->head->data;
}
**显示栈内数据**
// An highlighted block
void LinkStackShow(LinkStack *pst)
{
LinkStackNode *p = pst->head;
while(p != NULL)
{
printf("%d\\n", p->data);
p = p->next;
}
}
**摧毁栈**
// An highlighted block
void LinkStackDestroy(LinkStack *pst)
{
LinkStackNode *p = pst->head;
while(p != NULL)
{
pst->head = p->next;
free(p);
p = pst->head;
}
}
队列
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out)
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头
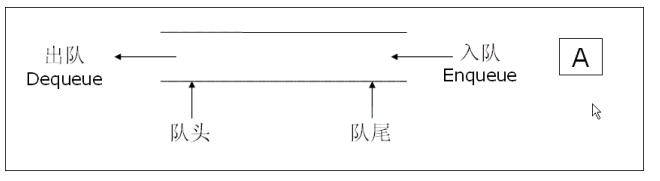
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。
顺序队列(循环队列)
结构:
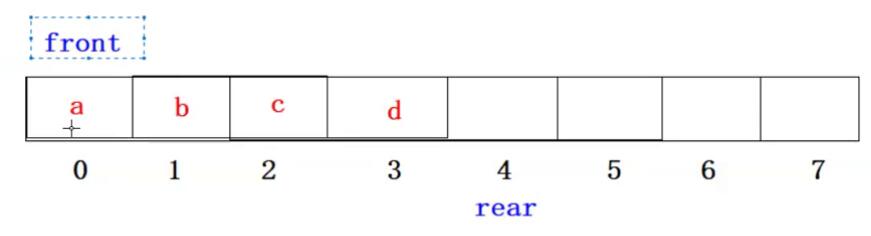
顺序队列在使用过程中容易出现虚假的满状态, 为了解决这个问题,就产生了一个较巧妙的方法,将顺序队列臆造为一个环状的空间,称之为循环队列。循环队列中指针和队列元素之间的关系不变,我们只需要利用模运算就可以很容易实现指针的循环移动。但是循环队列中存在一个问题,在循环队列中只凭头指针front等于尾指针rear无法判别队列空间是“空”还是“满”,可有两种处理方法:其一是另设一个标志位以区别队列是“空”还是“满”;其二是少用一个元素空间,约定以“队列头指针在队列尾指针的下一位置(指环状的下一位置)上”作为队列呈“满”状态的标志。此处使用方法二来解决这个问题。
循环队列的结构:

代码描述:
**顺序队列结构体定义**
// An highlighted block
typedef struct SeqQueue
{
ElemType *base;
size_t capacity;
int front;
int rear;
}SeqQueue;
**初始化**
// An highlighted block
void SeqQueueInit(SeqQueue *pq, int sz)
{
pq->capacity = sz;
pq->base = (ElemType*)malloc(sizeof(ElemType) * (pq->capacity+1)); //多出来的空间主要用于满和空状态的区分
assert(pq->base != NULL);
pq->front = pq->rear = 0;
}
**判断顺序队列是否满或空**
// An highlighted block
bool IsFull(SeqQueue *pq)
{
return (pq->rear+1)%(pq->capacity+1) == pq->front;//取模操作
}
bool IsEmpty(SeqQueue *pq)
{
return pq->rear == pq->front;
}
**入队**
// An highlighted block
void SeqQueuePush(SeqQueue *pq, ElemType v)
{
if(IsFull(pq))
{
printf("队列已满, %d不能入队.\\n", v);
return;
}
pq->base[pq->rear] = v;
pq->rear = (pq->rear + 1) % (pq->capacity+1);
}
**出队**
// An highlighted block
void SeqQueuePop(SeqQueue *pq)
{
if(IsEmpty(pq))
{
printf("队列已空,不能出队.\\n");
return;
}
pq->front = (pq->front + 1) % (pq->capacity+1);
}
**队头的元素**
// An highlighted block
ElemType SeqQueueFront(SeqQueue *pq)
{
if(IsEmpty(pq))
{
printf("队列已空,不能取队头元素.\\n");
return;
}
return pq->base[pq->front];
}
**队尾的元素**
// An highlighted block
ElemType SeqQueueBack(SeqQueue *pq)
{
if(IsEmpty(pq))
{
printf("队列已空,不能取队尾元素.\\n");
return;
}
return pq->base[(pq->rear-1+(pq->capacity+1)) % (pq->capacity+1)];
}
**顺序队列的元素**
// An highlighted block
void SeqQueueShow(SeqQueue *pq)
{
for(int i=pq->front; i!=pq->rear; )
{
printf("%d ", pq->base[i]);
i = (i+1) % (pq->capacity+1);
}
printf("\\n");
}
链队列
用链表表示的队列就简称为链队列。一个链队列显然需要两个分别指示队头和队尾的指针(分别称为头指针和尾指针)才能唯一确定。
结构:

代码描述:
**栈队列的结构体描述**
// An highlighted block
typedef struct LinkQueueNode
{
ElemType data;
struct LinkQueueNode *link;
}LinkQueueNode;
typedef struct LinkQueue
{
LinkQueueNode *front;
LinkQueueNode *rear;
}LinkQueue;
**初始化**
// An highlighted block
void LinkQueueInit(LinkQueue *pq)
{
pq->front = pq->rear = NULL;
}
**入队**
// An highlighted block
void LinkQueuePush(LinkQueue *pq, ElemType v)
{
LinkQueueNode *s = (LinkQueueNode*)malloc(sizeof(LinkQueueNode));
assert(s != NULL);
s->data = v;
s->link = NULL;
if(pq->front == NULL)
pq->front = pq->rear = s;
else
{
pq->rear->link = s;
pq->rear = s;
}
}
**出队**
// An highlighted block
void LinkQueuePop(LinkQueue *pq)
{
LinkQueueNode *p;
if(pq->front == NULL)
return;
p = pq->front;
pq->front = p->link;
free(p);
}
**队首和队尾元素**
// An highlighted block
ElemType LinkQueueFront(LinkQueue *pq)
{
if(pq->front == NULL)
return;
return pq->front->data;
}
ElemType LinkQueueBack(LinkQueue *pq)
{
if(pq->front == NULL)
return;
return pq->rear->data;
}
**展示所有元素**
// An highlighted block
void LinkQueueShow(LinkQueue *pq)
{
LinkQueueNode *p = pq->front;
while(p != NULL)
{
printf("%d ", p->data);
p = p->link;
}
printf("\\n");
}
整体代码
栈
**Stack.h**
**顺序栈和链栈**
// An highlighted block
#ifndef _STACK_H_
#define _STACK_H_
#include"Common.h"
#define SEQ_STACK_DEFAULT_SIZE 8
//顺序栈
typedef struct SeqStack
{
ElemType *base; //栈空间
size_t capacity;
size_t top; //栈顶指针
}SeqStack;
bool IsFull(SeqStack *pst);
bool IsEmpty(SeqStack *pst);
void SeqStackInit(SeqStack *pst, int sz);
void SeqStackPush(SeqStack *pst, ElemType v);
void SeqStackPop(SeqStack *pst);
ElemType SeqStackTop(SeqStack *pst);
//void SeqStackTop(SeqStack *pst, ElemType *v);
void SeqStackShow(SeqStack *pst);
void SeqStackDestroy(SeqStack *pst);
bool IsFull(SeqStack *pst)
{
return pst->top >= pst->capacity;
}
bool IsEmpty(SeqStack *pst)
{
return pst->top == 0;
}
void SeqStackInit(SeqStack *pst, int sz)
{
pst->capacity = sz > SEQ_STACK_DEFAULT_SIZE ? sz : SEQ_STACK_DEFAULT_SIZE;
pst->base = (ElemType *)malloc(sizeof(ElemType) * pst->capacity);
assert(pst->base != NULL);
pst->top = 0;
}
void SeqStackPush(SeqStack *pst, ElemType v)
{
if(IsFull(pst))
{
printf("栈已满,%d不能入栈.\\n", v);
return;
}
pst->base[pst->top++] = v;
}
void SeqStackPop(SeqStack *pst)
{
if(IsEmpty(pst))
{
printf("栈已空,不能出栈.\\n");
return;
}
pst->top--;
}
ElemType SeqStackTop(SeqStack *pst)
//void SeqStackTop(SeqStack *pst, ElemType *v) //出参
{
if(IsEmpty(pst))
{
printf("栈已空,没有栈顶元素.\\n");
return;
}
return pst->base[pst->top-1];
//*v = pst->base[pst->top-1];
}
void SeqStackShow(SeqStack *pst)
{
for(int i=pst->top-1; i>=0; --i)
printf("%d\\n", pst->base[i]);
}
void SeqStackDestroy(SeqStack *pst)
{
free(pst->base);
pst->base = NULL;
pst->capacity = pst->top = 0;
}
//链栈
typedef struct LinkStackNode
{
ElemType data数据结构学习笔记(栈队列OJ题)整体与总结