数据结构与算法学习笔记 栈和队列Ⅰ
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法学习笔记 栈和队列Ⅰ相关的知识,希望对你有一定的参考价值。
数据结构与算法学习笔记(5) 栈和队列
一.栈和队列的定义和特点
-
栈和队列是只能在表的“端点”进行插入和删除操作的线性表
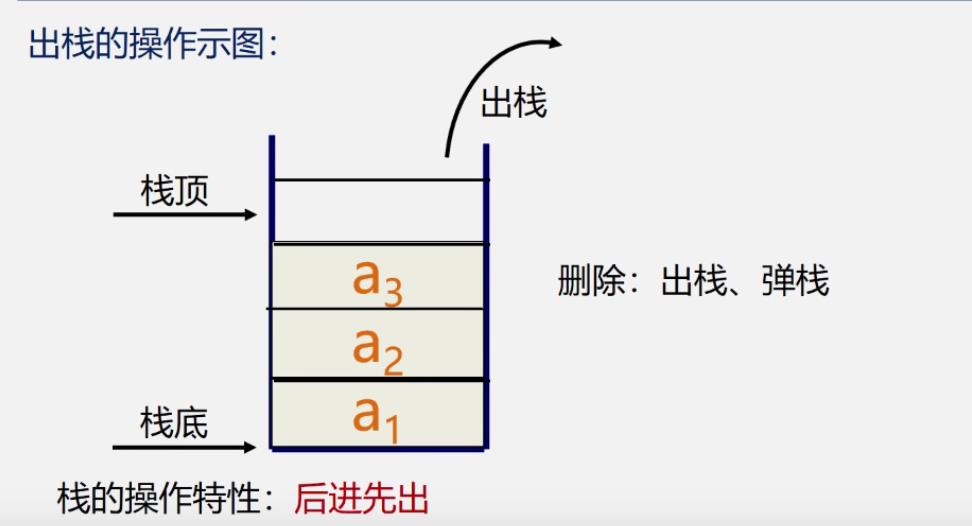
- 栈:后进先出
- 只能在尾部插入和删除
- 队列:先进先出
- 只能在尾部插入,头部删除

- 栈和队列是线性表的子集
- 是插入和删除位置受限的线性表
- 栈:后进先出
-
栈的应用

-
队列的应用

1.栈的定义和特点
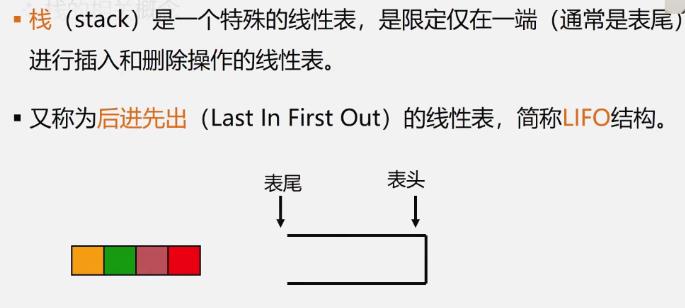
相关概念
-
表尾( a n a_n an端)称为栈顶(Top)
-
表头( a 1 a_1 a1端)称为栈底(Base)
-
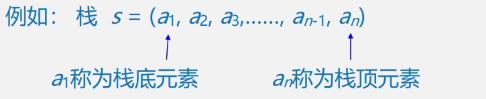
-
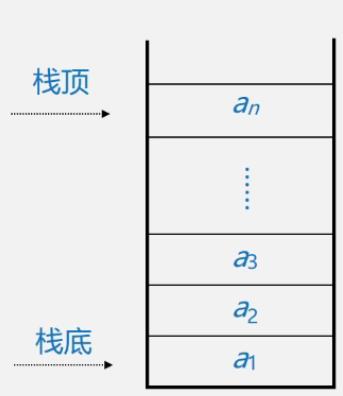
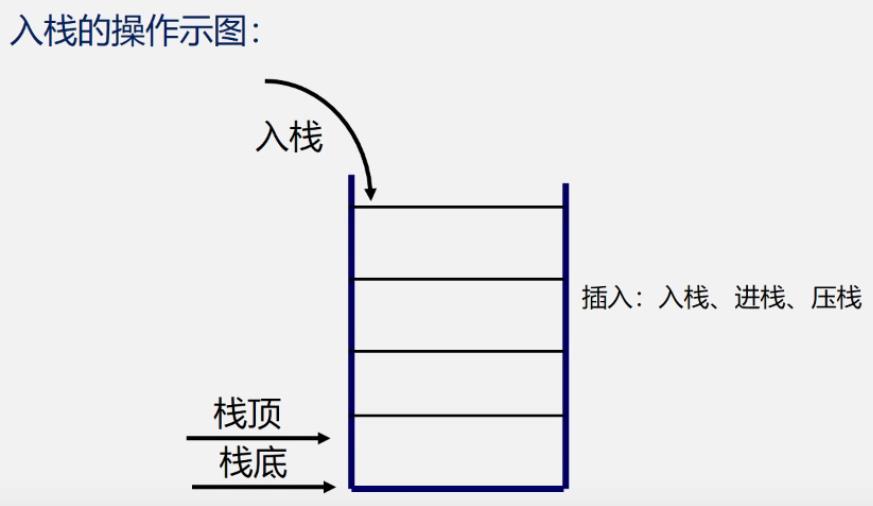
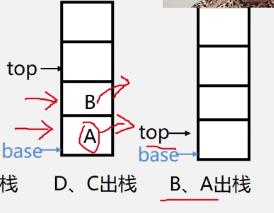
入栈
- 插入元素到栈顶(即表尾)的操作
-
出栈
- 从栈顶(即表尾)删除最后一个元素的操作>

示意图
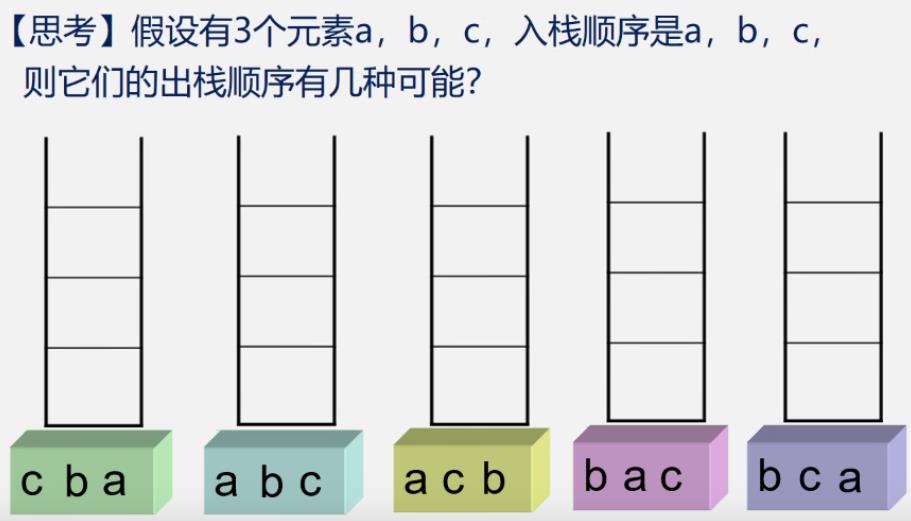
不可能得到cab的情况
栈与一般线性表的不同

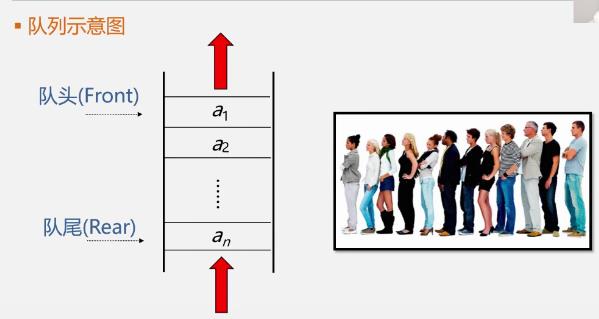
2.队列的定义和特点

相关概念

二.案例引入
1.栈的典型案例
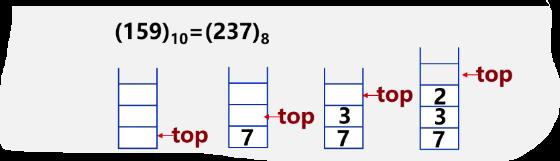
进制转换

-
例
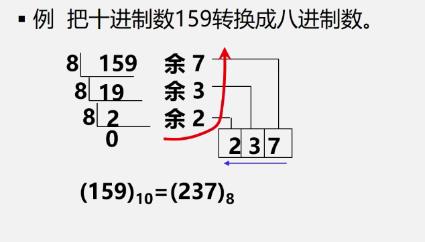
-
演示图
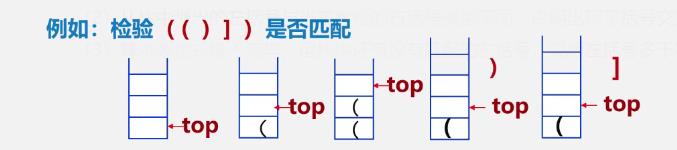
括号匹配的检验

-
检验规则

-
例
表达式求值


-
实现

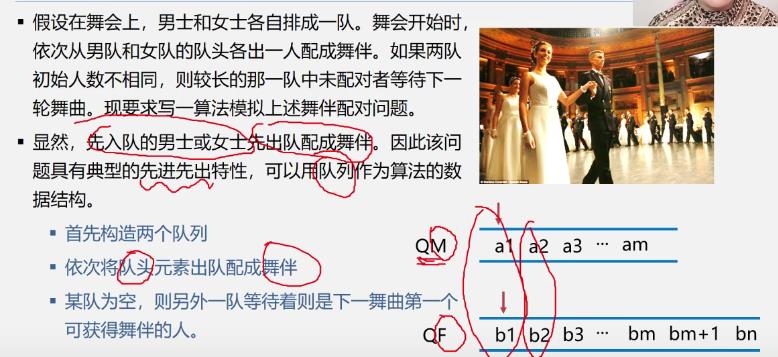
2.队列的典型案例
舞伴问题
三.栈的表示和操作的实现
1.栈的抽象数据类型定义
ADT Stack{
数据对象:
D = {ai|ai∈ElemSet,i=1,2,...,n,n≥0}
数据关系:
R1 = {<ai-1,ai>|ai-1,ai∈D,i=2,...,n}
约定an端为栈顶,a1端为栈底
基本操作: 初始化、进栈、出栈、取栈顶元素等
}ADT Stack
基本操作概述

- 栈本身就是线性表,所以栈也有顺序存储和链式存储两种实现方式
- 栈的顺序存储–顺序栈
- 栈的链式存储–链栈
2.顺序栈的表示和实现

-
入栈
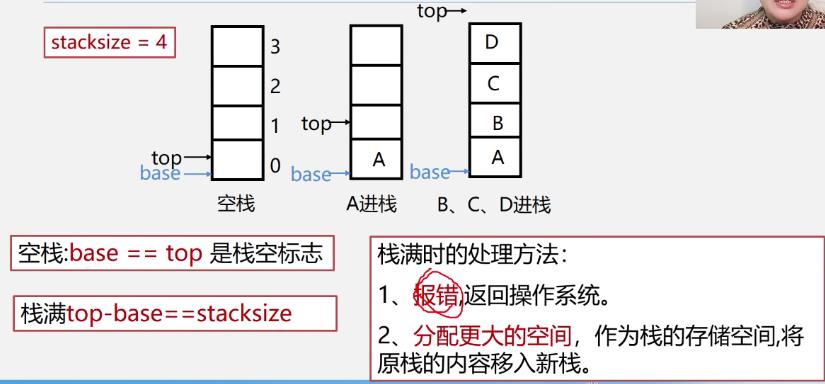
-
出栈
-
顺序栈特点

#define MAXSIZE 100
typedef struct{
SElemType *base;//栈底指针
SElemType *top;//栈顶指针
int stacksize; //栈可用最大容量
}SqStack;
-
小例

顺序表的初始化
Status InitStack(SqStack &S){ //构造一个空栈
S.base = new SElemType[MAXSIZE];
//或S.base = (SElemType*)malloc(MAXSIZE*sizeof(SElemType));
if (!S.base) exit(OVERFLOW); //存储空间分配失败
//分配成功
S.top = S.base; //栈顶指针等于栈底指针
S.stacksize = MAXSIZE;
return OK;
}
判断栈是否为空
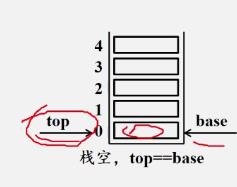
Status StackEmpty(SqStack S){
if(S.top == S.base){
return TRUE;
}
else
return FALSE;
}
求顺序栈的长度
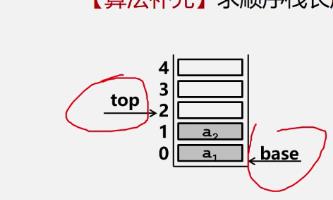
int StackLength(SqStack S){
return S.top - S.base;
}
清空顺序栈
Status ClearStack(SqStack S){
if(S.base) //如果栈不为空 就把top指针指向栈底
S.top = S.base;
return OK;
}
销毁顺序栈
Status DestropStack(SqStack &S){
if(S.base){
delete S.base; //释放空间,没有销魂指针
S.stacksize = 0;
S.base = S.top = NULL; //不置空的话会变为野指针
}
return OK;
}
顺序栈的入栈
要判断是否已经栈满

Status Push(SqStack &S,SElemType e){
if(S.top-S.base==S.stacksize)//栈满
return ERROR;
*S.top = e;
S.top++;
//也可以合并为一个语句 *S.top++=e;
return OK;
}
顺序栈的出栈
要注意栈空的情况

Status Pop(SqStack &S ,SElemType &e){
//若栈不空,则删除S的栈顶元素
if(S.top == S.base) //等价于 if(StackEmpty(S))
return ERROR;
--S.top;
e=*S.top;
//可合并为e=*--S.top;
return OK;
}
3.链栈的表示和实现
-
链栈是运算受限的单链表,只能在链表头部进行操作
-
类型定义
typedef struct StackNode{ SElemType data; struct StackNode *next; }StackNode, *LinkStack; LinkStack S; //指向 struct StackNode 的指针型结构类型 struct StackNode是栈的结点
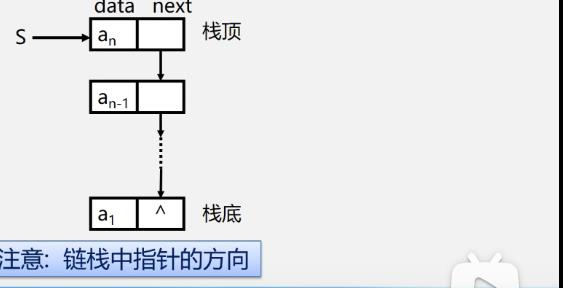
链栈中的指针和普通单链表的指针方向不同
- 链栈的特点
- 链栈的头指针就是栈顶
- 不需要头结点
- 基本不存在栈满的情况
- 空的链栈相当于头指针指向空
- 插入和删除仅在栈顶处执行
链栈的初始化
void InitStack(LinkStack &S){
//构造一个空栈,栈顶指针置为空
S=NULL;
return OK;
}
判断链栈是否为空
Status StackEmpty(LinkStack S){
if(S==NULL) return TRUE;
else return FALSE;
}
链栈的入栈
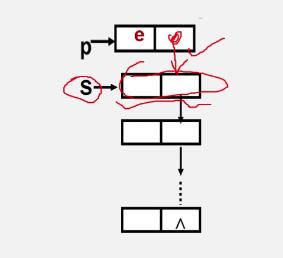
Status Push(LinkStack &S,SElemType e){
p = new StackNode; //生成新结点p
p->data = e; //新结点数据域置为e
p->next = S; //新结点插入栈顶
S = p; //修改栈顶指针
}
链栈的出栈
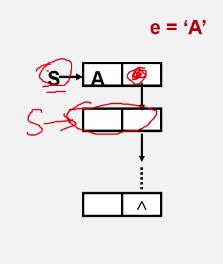
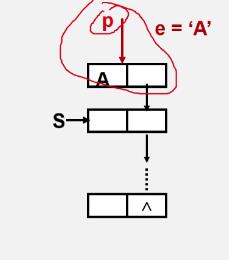
Status Pop(LinkStack &S,SElemType &e){
if(S==NULL) return ERROR;
e = S->data;
p = S;
S= S->next;
delete p;
return OK;
}
取栈顶元素
SElemType GetTop(LinkStack S){
if(S!=NULL)
return S->data;
}
四.队列的表示和操作的实现
1.队列的抽象数据类型定义

-
队列的两种物理存储方式
- 队列的物理存储可以用顺序存储结构,也可以用链式存储结构
- 即顺序队列和链式队列
-
队列的顺序表示 :用一维数组base[MAXQSIZE]
#define MAXQSIZE 100 //最大队列长度 Typedef struct{ QElemType *base; //初始化的动态分配存储空间 //数据的元素类型QElemType,base指针指向数组的首元素, 之后可以分配空间 int front; //用于表示队头元素的下标 int rear; //用于表示队尾元素的下标 }SqQueue;
2.队列的顺序表示和实现(顺序队)
一般顺序队的问题
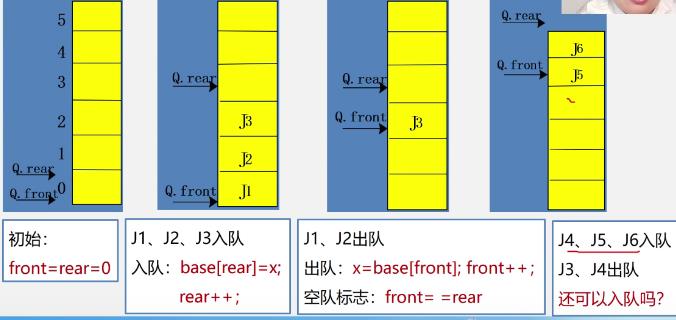
图中问题:没法入队了
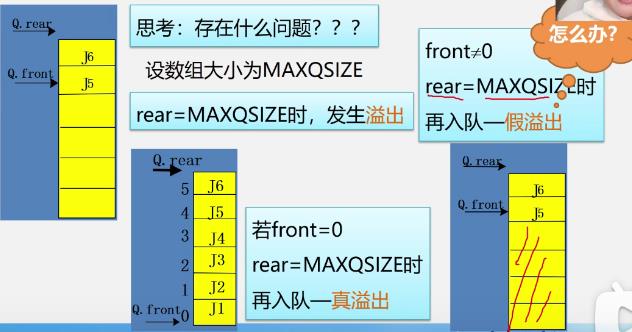
上图中的假溢出就是说,其实数组中还有存储空间,但是却没法入队了,
解决办法:循环队列


区别队空队满
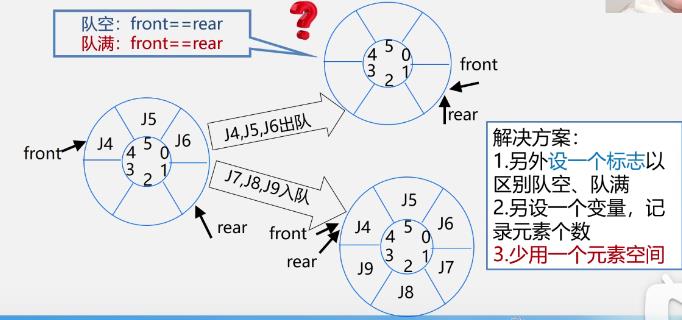
循环队列解决队满时判断方法–少用一个元素空间

循环队列的类型定义
#define MAXQSIZE 100 //最大队列长度
typedef struct{
QElemType *base; //动态分配存储空间
int front; //头指针(不是真的指针,就是表示头元素下标) 若队列不空,指向队列头元素
int rear; //尾指针(不是真的指针),若队列不空,指向队列尾元素的下一个位置
}SqQueue;
循环队列的操作
队列初始化
Status InitQueue(SqQueue &Q){
Q.base = new QElemType[MAXQSIZE] //分配数组空间
//C语法 Q.base=(QElemType*)malloc(MAXQSIZE*sizeof(QElemType));
//Q.base是指针,数组首元素的地址就是指针
if(!Q.base) exit(OVERFLOW); //存储分配失败
Q.front=Q.rear=0; //分配成功,头指针尾指针置为0,队列为空
}
求队列长度
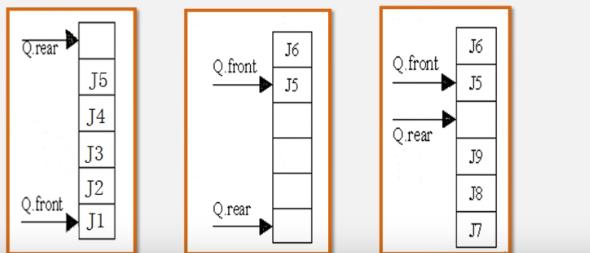
第一个图可以直接用Q.rear-Q.front, 第二张就不能直接减了
int QueueLength (SqQueue Q){
return((Q.rear-Q.front+MAXQSIZE)%MAXQSIZE);
}
循环队列入队
牺牲了一个存储空间的情况下(少用一个元素空间解决队空队满判断)
Status EnQueue(SqQueue &Q, QElemType e){
if((Q.rear+1)%MAXSIZE == Q.front) return ERROR; //队满
Q.base[Q.rear]=e; //新元素加入队尾
Q.rear=(Q.rear+1)%MAXQSIZE; //尾指针+1取模
return OK;
}
循环队列出队

Status DeQueue (SqQueue &Q,QElemType &e){
if(Q.front == Q.rear) return ERROR; //队空
e = Q.base[front]; //保存队头元素
Q.front = (Q.front+1)%MAXQSIZE; //队头指针+1
return OK;
}
取队头元素
SElemType GetHead(SqQuere Q){
if(Q.front!=Q.rear) //队列不为空
return Q.base[Q.front]; //返回队头指针元素的值,队头指针不变
}
3.队列的链式表示和实现(链队)
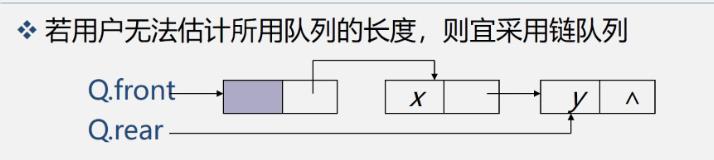
链队列的类型定义
#define MAXQSIZE 100 //最大队列长度
typedef struct Qnode{
QElemType data;
struct Qnode *next;
}QNode,*QueuePtr;
pointer简写ptr
typedef struct{
QuenePtr front; //队头指针
QuenePtr rear; //队尾指针
}LinkQueue; //链式队列
链队列运算指针变化状况
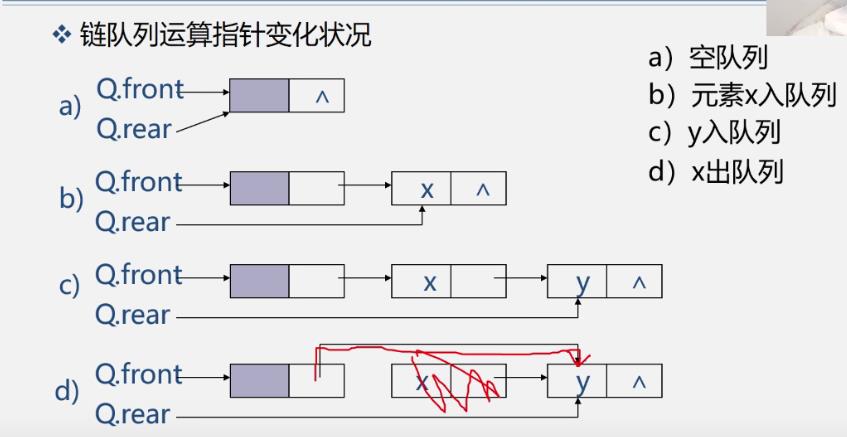
链队列的操作
链队列的初始化

Status InitQueue(LinkQueue &Q){
Q.front = Q.rear =(QueuePtr)malloc(sizeof(QNode));
if(!Q.front) exit(OVERFLOW);
Q.front->next=NULL;
return OK;
}
链队列的销毁
-
算法思想:
从队头结点开始,依次释放所有结点

-
算法描述
Status DestroyQueue(LinkQueue &Q){ while(Q.front){ p=Q.front->next; free(Q.front); //释放结点的那块空间 Q.front=p; //p那里可以用尾指针来代替 //Q.rear=Q.front->next; //free(Q.front); //Q.front=Q.rear; } retrun OK; }
元素e入队

Status EnQueue(LinkQueue &Q,QElemType e){
p=(QueuePtr)malloc(sizeof(QNode));
if(!p) exit(OVERFLOW);
//空间分配成功
p->data=e;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}
链队列出队
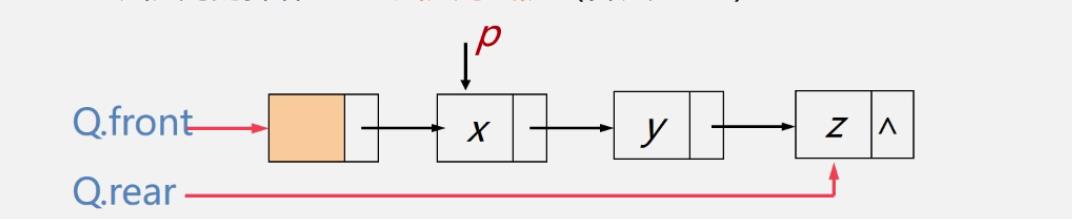
p指向头结点的下一元素

Status DeQueue(LinkQueue &Q,QElemType &e){
if(Q.front==Q.rear) return ERROR;
p=Q.front->next;
e=p->data;
Q.front->next=p->next;
if(Q.rear==p) Q.rear=Q.front; //如果删除的是尾结点
delete p;
return OK;
}
取链队列的队头元素
Status GetHead(LinkQueue Q,QElemType &e){
if(Q.front==Q.rear) return ERROR;
e=Q.front->next->data;
return OK;
}
if(!p) exit(OVERFLOW);
//空间分配成功
p->data=e;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}
以上是关于数据结构与算法学习笔记 栈和队列Ⅰ的主要内容,如果未能解决你的问题,请参考以下文章