深度学习与图神经网络核心技术实践应用高级研修班-Day2股票预测（stock_prediction）

Posted 2021-09-08 ZSYL

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了深度学习与图神经网络核心技术实践应用高级研修班-Day2股票预测（stock_prediction）相关的知识，希望对你有一定的参考价值。

股票预测

1. 股票预测背景
2. 股票数据来源
3. 股票数据预处理
4. 同步预测
5. 同步预测效果
6. 异步预测
7. 完整展示

1. 股票预测背景

股票价格是典型的时间序列数据（简称时序数据），会受到经济环境、政府政策、人为操作多种复杂因素的影响。
不像气象数据那样具备明显的时间和季节性模式，例如一天之内和一年之内的去气温变化等。
以股票价格为例，介绍如何对时序数据进行预测。

2. 股票数据来源

S&P 500 股价数据爬取自 Google Finance API，已进行过缺失值处理。

3. 股票数据预处理

用pandas读取 csv 文件为 DataFrame，利用该库查看特征
的数值分布以及概要。

数据共 502 列，41266行，502 列分别为：
- DATE：该行数据的时间戳；
- SP500：大盘指数；
- 其他：可以理解为 500 支个股的股价。

4. 同步预测

同步预测：使用当前时刻的 500 支个股股价，预测当前时刻的大盘指数，即⼀个回归问题，输入共 500 维特征，输出⼀维，即 [None, 500] ⇒ [None, 1]。

使用TensorFlow实现同步预测，主要用到多层感知机，
损失函数用均方误差。

5. 同步预测效果

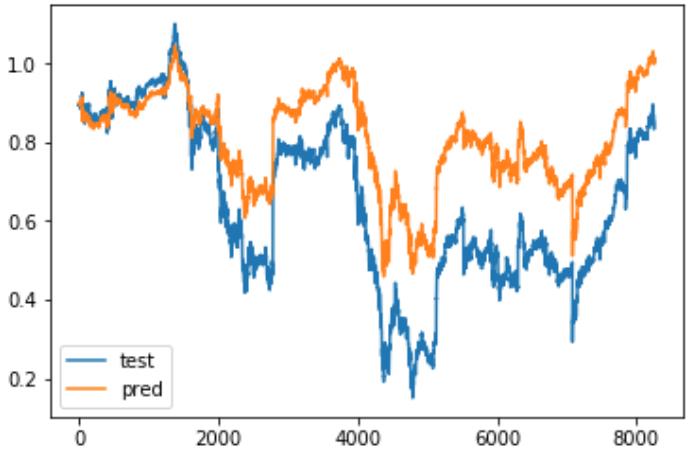
6. 异步预测

异步预测：使用历史若干个时刻的大盘指数，预测当前时
刻的大盘指数，这样才更加符合预测的定义。

例如，使用历史若干个时刻的 500 支个股股价以及大盘指
数，预测当前时刻的大盘指数，即 [None, 5, 501] ⇒ [None, 1]。

使用Keras实现异步预测，主要用到RNN中的 LSTM。

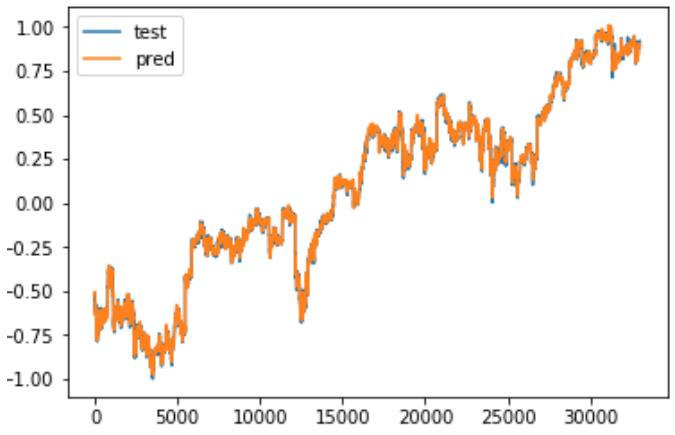
7. 完整展示

# https://github.com/sebastianheinz/stockprediction
# https://medium.com/mlreview/a-simple-deep-learning-model-for-stock-price-prediction-using-tensorflow-30505541d877

# select gpu
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '3'

# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.preprocessing import MinMaxScaler
import time

from tensorflow import keras
from tensorflow.keras.layers import Dense, LSTM
from tensorflow.keras.models import Sequential
from tensorflow.keras.losses import MSE
from tensorflow.keras.optimizers import Adam

# read stacks data
data = pd.read_csv('data_stocks.csv')
data.describe()

	DATE	SP500	NASDAQ.AAL	NASDAQ.AAPL	NASDAQ.ADBE	NASDAQ.ADI	NASDAQ.ADP	NASDAQ.ADSK	NASDAQ.AKAM	NASDAQ.ALXN	...	NYSE.WYN	NYSE.XEC	NYSE.XEL	NYSE.XL	NYSE.XOM	NYSE.XRX	NYSE.XYL	NYSE.YUM	NYSE.ZBH	NYSE.ZTS
count	4.126600e+04	41266.000000	41266.000000	41266.000000	41266.00000	41266.000000	41266.000000	41266.000000	41266.000000	41266.000000	...	41266.000000	41266.000000	41266.000000	41266.000000	41266.000000	41266.000000	41266.000000	41266.000000	41266.000000	41266.000000
mean	1.497749e+09	2421.537882	47.708346	150.453566	141.31793	79.446873	103.480398	102.998608	50.894352	122.981163	...	97.942211	104.740666	46.664402	43.043984	80.784595	19.300718	54.541988	71.757891	121.423515	60.183874
std	3.822211e+06	39.557135	3.259377	6.236826	6.91674	2.000283	4.424244	9.389788	4.833931	11.252010	...	5.411795	10.606694	1.508444	1.714533	1.840989	11.686532	3.526321	4.038272	5.607070	3.346887
min	1.491226e+09	2329.139900	40.830000	140.160000	128.24000	74.800000	95.870000	83.000000	44.650000	96.250000	...	83.410000	89.510000	44.090000	39.120000	76.060000	6.660000	48.820000	63.180000	110.120000	52.300000
25%	1.494432e+09	2390.860100	44.945400	144.640000	135.19500	78.030000	101.300000	94.820000	47.440000	116.950000	...	95.960000	95.010000	45.155000	41.955000	80.220000	7.045000	51.630000	69.110000	117.580000	59.620000
50%	1.497638e+09	2430.149900	48.360000	149.945000	142.26000	79.410000	102.440000	106.820000	49.509900	123.620000	...	99.250000	99.660000	46.810000	43.200000	81.150000	27.890000	53.850000	73.470000	120.650000	61.585600
75%	1.501090e+09	2448.820100	50.180000	155.065000	147.10000	80.580000	104.660000	110.490000	52.230000	132.218800	...	102.080000	117.034700	47.730000	44.370000	82.062050	30.470000	57.140000	74.750000	126.000000	62.540000
max	1.504210e+09	2490.649900	54.475000	164.510000	155.33000	90.440000	121.770000	119.270000	62.560000	142.875000	...	106.375000	123.870000	49.660000	47.210000	83.630000	32.930000	62.130000	77.120000	133.450000	63.840000

8 rows × 502 columns

data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 41266 entries, 0 to 41265
Columns: 502 entries, DATE to NYSE.ZTS
dtypes: float64(501), int64(1)
memory usage: 158.0 MB

data.head()

	DATE	SP500	NASDAQ.AAL	NASDAQ.AAPL	NASDAQ.ADBE	NASDAQ.ADI	NASDAQ.ADP	NASDAQ.ADSK	NASDAQ.AKAM	NASDAQ.ALXN	...	NYSE.WYN	NYSE.XEC	NYSE.XEL	NYSE.XL	NYSE.XOM	NYSE.XRX	NYSE.XYL	NYSE.YUM	NYSE.ZBH	NYSE.ZTS
0	1491226200	2363.6101	42.3300	143.6800	129.6300	82.040	102.2300	85.2200	59.760	121.52	...	84.370	119.035	44.40	39.88	82.03	7.36	50.22	63.86	122.000	53.350
1	1491226260	2364.1001	42.3600	143.7000	130.3200	82.080	102.1400	85.6500	59.840	121.48	...	84.370	119.035	44.11	39.88	82.03	7.38	50.22	63.74	121.770	53.350
2	1491226320	2362.6799	42.3100	143.6901	130.2250	82.030	102.2125	85.5100	59.795	121.93	...	84.585	119.260	44.09	39.98	82.02	7.36	50.12	63.75	121.700	53.365
3	1491226380	2364.3101	42.3700	143.6400	130.0729	82.000	102.1400	85.4872	59.620	121.44	...	84.460	119.260	44.25	39.99	82.02	7.35	50.16	63.88	121.700	53.380
4	1491226440	2364.8501	42.5378	143.6600	129.8800	82.035	102.0600	85.7001	59.620	121.60	...	84.470	119.610	44.11	39.96	82.03	7.36	50.20	63.91	121.695	53.240

5 rows × 502 columns

print('begin', time.strftime('%Y-%m-%d', time.localtime(data['DATE'].min())))
print('end', time.strftime('%Y-%m-%d', time.localtime(data['DATE'].max())))

begin 2017-04-03
end 2017-09-01

plt.plot(data['SP500'])

# train : test = 0.8 : 0.2
data.drop('DATE', axis=1, inplace=True)
data_train = data.iloc[:int(data.shape[0] * 0.8), :]
data_test = data.iloc[int(data.shape[0] * 0.8):, :]
print('training data shape:', data_train.shape)
print('test data shape', data_test.shape)

training data shape: (33012, 501)
test data shape (8254, 501)

# scale data into the range for -1 to 1
scaler = MinMaxScaler(feature_range=(-1, 1))
scaler.fit(data_train)
data_train = scaler.transform(data_train)
data_test = scaler.transform(data_test)

X_train = data_train[:, 1:]
y_train = data_train[:, 0]
X_test = data_test[:, 1:]
y_test = data_test[:, 0]

# seq_len = 5
# X_train = np.array([data_train[i : i + seq_len, 0] for i in range(data_train.shape[0] - seq_len)]).squeeze()
# y_train = np.array([data_train[i + seq_len, 0] for i in range(data_train.shape[0] - seq_len)])
# X_test = np.array([data_test[i : i + seq_len, 0] for i in range(data_test.shape[0] - seq_len)]).squeeze()
# y_test = np.array([data_test[i + seq_len, 0] for i in range(data_test.shape[0] - seq_len)])

model = Sequential(layers=[
    Dense(1024, activation='relu', input_shape=X_train.shape[1:]),
    Dense(512, activation='relu'),
    Dense(256, activation='relu'),
    Dense(128, activation='relu'),
    Dense(1, activation='linear'),
])

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 1024)              513024    
_________________________________________________________________
dense_1 (Dense)              (None, 512)               524800    
_________________________________________________________________
dense_2 (Dense)              (None, 256)               131328    
_________________________________________________________________
dense_3 (Dense)              (None, 128)               32896     
_________________________________________________________________
dense_4 (Dense)              (None, 1)                 129       
=================================================================
Total params: 1,202,177
Trainable params: 1,202,177
Non-trainable params: 0
_________________________________________________________________

model.compile(optimizer=Adam(lr=0.001), loss=MSE)

from tensorflow.keras.callbacks import LambdaCallback

def on_epoch_end(epoch, logs):
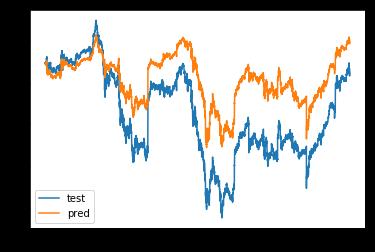
    y_pred = model.predict(X_test)
    plt.plot(y_test, label='test')
    plt.plot(y_pred, label='pred')
    plt.legend()
    plt.show()

model.fit(X_train, y_train,
          epochs=5,
          batch_size=256,
          shuffle=True,
          callbacks=[LambdaCallback(on_epoch_end=on_epoch_end)])

Epoch 1/5
32512/33012 [============================>.] - ETA: 0s - loss: 0.0101

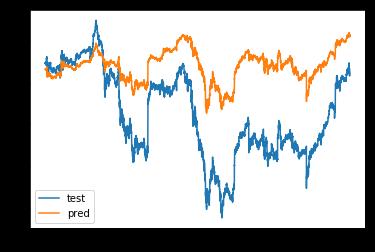
33012/33012 [==============================] - 2s 73us/step - loss: 0.0099
Epoch 2/5
32768/33012 [============================>.] - ETA: 0s - loss: 1.7015e-04

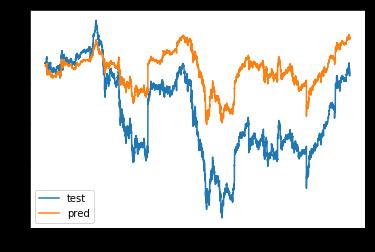
33012/33012 [==============================] - 1s 42us/step - loss: 1.6941e-04
Epoch 3/5
32000/33012 [============================>.] - ETA: 0s - loss: 2.1466e-04

33012/33012 [==============================] - 1s 42us/step - loss: 2.1038e-04
Epoch 4/5
31488/33012 [===========================>..] - ETA: 0s - loss: 1.1966e-04

33012/33012 [==============================] - 1s 44us/step - loss: 1.1896e-04
Epoch 5/5
32000/33012 [============================>.] - ETA: 0s - loss: 2.0731e-04

33012/33012 [==============================] - 1s 44us/step - loss: 2.0534e-04

from tensorflow.keras.layers import Input, Dense, CuDNNLSTM, InputLayer
from tensorflow.keras.models import Sequential

seq_len = 5
X_train = np.array([data_train[i : i + seq_len, 1:] for i in range(data_train.shape[0] - seq_len)])#[:, :, np.newaxis]
y_train = np.array([data_train[i + seq_len, 0] for i in range(data_train.shape[0] - seq_len)])
X_test = np.array([data_test[i : i + seq_len, 1:] for i in range(data_test.shape[0] - seq_len)]) #[:, :, np.newaxis]
y_test = np.array([data_test[i + seq_len, 0] for i in range(data_test.shape[0] - seq_len)])

X_train.shape

(33007, 5, 500)

lstm_model = Sequential(layers=[
    InputLayer(input_shape=X_train.shape[1:]),
    CuDNNLSTM(128),
    Dense(1, activation='linear'),
])

lstm_model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
cu_dnnlstm (CuDNNLSTM)       (None, 128)               322560    
_________________________________________________________________
dense_5 (Dense)              (None, 1)                 129       
=================================================================
Total params: 322,689
Trainable params: 322,689
Non-trainable params: 0
_________________________________________________________________

lstm_model.compile(loss=MSE, optimizer=Adam())

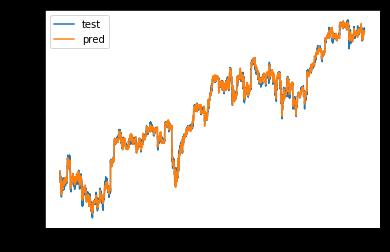
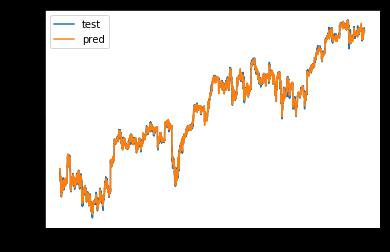
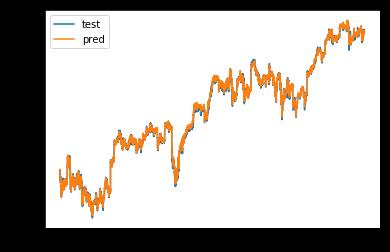
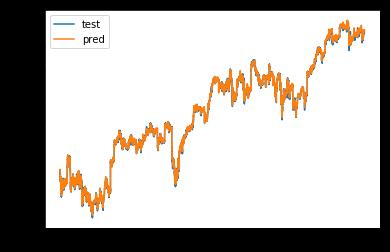
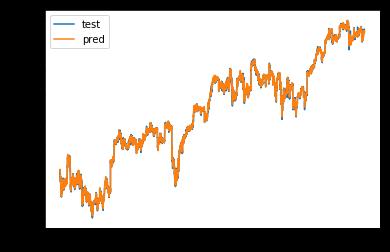
def on_epoch_end(epoch, logs):
    y_pred = lstm_model.predict(X_train)
    plt.plot(y_train, label='test')
    plt.plot(y_pred, label='pred')
    plt.legend()
    plt.show()

lstm_model.fit(X_train, y_train,
          epochs=5,
          batch_size=256,
          shuffle=True,
          callbacks=[LambdaCallback(on_epoch_end=on_epoch_end)]
              )

Epoch 1/5
32512/33007 [============================>.] - ETA: 0s - loss: 0.0197

33007/33007 [==============================] - 3s 101us/step - loss: 0.0194
Epoch 2/5
32256/33007 [============================>.] - ETA: 0s - loss: 3.2466e-04

33007/33007 [==============================] - 3s 80us/step - loss: 3.2286e-04
Epoch 3/5
31744/33007 [===========================>..] - ETA: 0s - loss: 2.3210e-04

33007/33007 [==============================] - 3s 80us/step - loss: 2.3420e-04
Epoch 4/5
32512/33007 [============================>.] - ETA: 0s - loss: 2.0556e-04

33007/33007 [==============================] - 3s 76us/step - loss: 2.0526e-04
Epoch 5/5
31488/33007 [===========================>..] - ETA: 0s - loss: 1.9163e-04

33007/33007 [==============================] - 3s 80us/step - loss: 1.9080e-04

<tensorflow.python.keras.callbacks.History at 0x7f7f2852bf98>

附：

%matplolib inline  # 在jupyter notebook上面显示图片

以上是关于深度学习与图神经网络核心技术实践应用高级研修班-Day2股票预测（stock_prediction）的主要内容，如果未能解决你的问题，请参考以下文章

深度学习与图神经网络核心技术实践应用高级研修班-Day3迁移学习（Transfer Learning）

深度学习与图神经网络核心技术实践应用高级研修班-Day1典型深度神经网络模型

深度学习与图神经网络核心技术实践应用高级研修班-Day1Tensorflow和Pytorch

深度学习与图神经网络核心技术实践应用高级研修班-Day2基于Keras的深度学习程序开发

深度学习与图神经网络核心技术实践应用高级研修班-Day1受限波尔兹曼机和深度信念网络

深度学习与图神经网络核心技术实践应用高级研修班-Day4深度强化学习（Deep Q-learning）